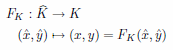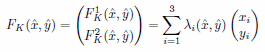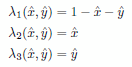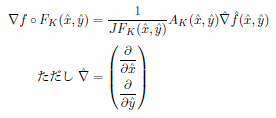前へ | 偏微分方程式解法用のメッシュ生成トップへ | 次へ
4. 三角形、線形近似
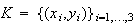 を
を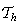 (
(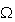 の三角形分割(triangulation))の一つの要素とする。また
の三角形分割(triangulation))の一つの要素とする。また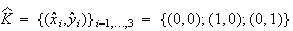 を参照要素、
を参照要素、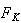 をすべての
をすべての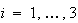 について
について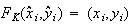 とするような
とするような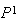 変換とする。
変換とする。
従って
|
|
|
と書ける。ここに
|
|
|
であり、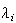 は
は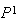 の要素で
の要素で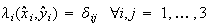
|
|
|
を満たすものとする。
変換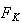 は集合
は集合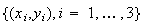 のどの3点も一直線上になければ全単射(bijective function)である。この変換のヤコビアンは
のどの3点も一直線上になければ全単射(bijective function)である。この変換のヤコビアンは
|
|
|
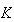 上で定義される関数
上で定義される関数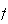 に対し、
に対し、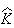 上の関数を
上の関数を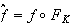 のように定義する。
のように定義する。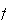 は、
は、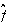 が
が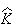 上の
上の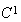 関数であり、次の等式が成り立つ場合に限り、
関数であり、次の等式が成り立つ場合に限り、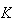 上での
上での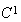 関数となる点に注意。
関数となる点に注意。
|
|
|
質量行列、剛性行列への要素からの寄与の計算は次の公式を用いてアイソパラメトリックに計算することができる。
|
|
(7) |
|
|
|
|
|
(8) |
ここに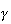 と
と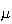 は要素
は要素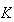 で定義される、例えば
で定義される、例えば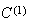 関数である。最後に
関数である。最後に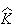 上での積分を計算するには
上での積分を計算するには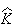 上での積分公式を用いれば良い。
上での積分公式を用いれば良い。