���̋L���� nAG �œK���R�[�i�[ �V���[�Y�̈ꕔ�ł��B
�����FCalibrate the Heston model faster using derivative-free optimization techniques
���̋L���ł́A���Z�ƊE�ŕp�o����L�����u���[�V�������i�s��f�[�^�ɑ���I�v�V�����v���C�V���O���f���̃L�����u���[�V�����j���A�����𗘗p���Ȃ��œK���iDerivative-free optimization�GDFO�j��p���č�����������@���Љ�܂��B
�ȉ��̎����́AnAG ���J�Â����E�F�r�i�[�Ɋ�Â��Ă��܂��i�^��� �������j�B
DFO �\���o�[�̍ŋ߂̉��Ǔ_
nAG �́A�I�b�N�X�t�H�[�h��w�� Coralia Cartis ���A�Ȃ�т� Lindon Roberts ���Ƌ����Ō������s���܂����B���̌����ɂ��A�m�C�Y�ϐ���A�\�������ɑ����ԃ��f���̋����ȂǁA�d�v�ȉ��P���Ȃ���ADFO �̍Ő�[�Z�p [1] �� nAG ���C�u�����ɓ�������܂����B���݁A�f�[�^�t�B�b�e�B���O���ɓK�������E����t������`�ŏ����\���o�[ handle_solve_dfls�ie04ff�j�ƁA��ʓI�Ȕ���`����ΏۂƂ��� handle_solve_dfno�ie04jd�j����Ă��܂��B�܂��A���l���\���o�[�ɓn�����߂̑�փC���^�[�t�F�[�X�ireverse communication�j�Ahandle_solve_dfls_rcomm�ie04fg�j�� handle_solve_dfno_rcomm�ie04je�j�����ꂼ����Ă��܂��B
���[���s�A���I�v�V�����̃v���C�V���O�FHeston ���f���̃L�����u���[�V����
���[���s�A���I�v�V�����́A�����Y���A��߂�ꂽ�����i�������j�ɁA��߂�ꂽ���i�i�s�g���i�j�ŁA�w���i�R�[���j�܂��́A���p�i�v�b�g�j���錠���i�I�v�V�����j���A������ɕt�^����_��ł��B�I�v�V�����v���C�V���O�́A�������ɔ����肪�I�v�V�������s�g����m���Ɋ�Â��ĉ��i�����肵�܂��B
���N�ɂ킽��A�����̐��l�I�ȉ��i����@����������Ă��܂������A�ł���ʓI�Ȃ��̂́A���Ȃ��ABlack-Scholes �������Ɋ�Â��Ă��܂��B�������ABlack-Scholes ���f���ɂ͂������̌��_������A���ł��{���e�B���e�B�����ԓI�Ɉ��ł���Ƃ������肪����܂��B���ۂɂ́A�s��̃C���v���C�h�{���e�B���e�B�̓X�}�C���J�[�u�ł��邱�Ƃ��ϑ�����Ă��܂��B���̌`���������邽�߂ɁAHeston �̂悤�Ȋm���I�{���e�B���e�B���f������������܂����B���̃��f���͈ȉ��̕������ō\������Ă��܂��F
�����ŁA$S_t$ �͌����Y�̃X�|�b�g���i�A$v_t$ �͎��Ԉˑ��̃{���e�B���e�B�A$(dW_t^1, dW_t^2)$ �͂Q�̃u���E���^���ł��B
���̃��f���́A�s��Œ��ڊϑ����邱�Ƃ��e�ՂłȂ��S�̃p�����[�^�[�A���Ȃ킿�A�{���e�B���e�B�X�P�[�����O $\sigma$�A���ω�A�� $\lambda$�A�{���e�B���e�B�̃{���e�B���e�B $\alpha$�A�u���E���^���̑��� $\rho$ �Ɉˑ����Ă��܂��B�]���āA�����̃p�����[�^�[���i�L�����u���[�g�j����K�v������܂��B����́A�ߋ��̃f�[�^���ώ@���A��X�̃��f���\�����\�Ȍ��肻��Ɉ�v����悤�ɁA�p�����[�^�[�̍œK�������݂邱�Ƃł��B�����āA����́A�e�Ղɗ��p�ł���f���o�e�B�u���Ȃ��A��r�I�����ȕ]���ł��邽�߁ADFO �ɍœK�Ȗ��ł��B
Heston ���f���ɂ�������ԍ\���̓���
Heston �������́A�S�̃p�����[�^�[�����Ԃɑ��Ĉ��ł��邱�Ƃ����肵�Ă��܂����A����͕K�������s��̌����ɑΉ����Ă��܂���B���̖����y�����邽�߂ɁA���ԍ\�������܂��B�܂�A$\sigma$�A$\lambda$�A$\alpha$�A$\rho$ �����̊��Ԃɂ����Ă݈̂��ƌ��Ȃ��܂��B����ɂ���āA���f���́A�s��̓��������ǂ��͕�ł���悤�ɂȂ�܂����A��������p�����[�^�[�̐����l��������Ԃ̐����������܂��B
�Ȃ��A���ԍ\�������� Heston ���f���̎����́AnAG ���C�u�����iopt_heston_term�As30ncf�j�ŗ��p�\�ł��B����́A�ȉ��̐��l�����Ŏg�p����Ă��܂��B
�L�����u���[�V�������̐ݒ�
�s��f�[�^�Ƃ��āA2012 �N���� 2016 �N�܂ł̒ʉ݃y�A EUR-USD �̊O���ב֎s��̃q�X�g���J���f�[�^���g���܂��B�e���t�ɂ��āA�V�̖����i2m�A3m�A6m�A1y�A2y�A3y�A5y�j�̃f�[�^������܂��F
- EUR ���X�N�t���[���[�g
- USD ���X�N�t���[���[�g
- 25-$\Delta$ RR �N�H�[�g
- 25-$\Delta$ BF �N�H�[�g
- ATM �N�H�[�g
���̃f�[�^�̖��炩�Ȗ��_�̈�́A���ԍ\�����l�����Ȃ��Ă��A�R�̃N�H�[�g�ƂS�̃p�����[�^�[���������ł��Ȃ����Ƃł��B�I�[�o�[�t�B�b�e�B���O������邽�߁A�������̐��l�������s������A�p�����[�^�[�̂P�� $\lambda$ �����l�ɌŒ肷�邱�Ƃɂ��܂����B���ԍ\�����l�����Ȃ���AHeston ���f���̃L�����u���[�V�����́A����`�ŏ����œK�������������ƂɋA�����܂��F
�����ŁA$H_i(\alpha,\rho,\sigma)$ �̓��f���ɂ���ė\�����ꂽ���i�A$M_i^{market}$ �͎��ۂ̃f�[�^�ł��B
���̃X�e�b�v�́A���ԍ\���ɐݒ肷����Ԑ���I�����邱�Ƃł��B�������V�邽�߁A���ԍ\���ɂV�̊��Ԃ�ݒ肷��͎̂��R�Ȃ��Ƃł��B�e���t�ɂ��āA$k$ �Ԗڂ̖����ɑ��� $k$ �̊��Ԃ��l���܂��B
�܂��A���̍\���ł́A�e�������O�̖����̃p�����[�^�[�Ɉˑ����A����ɂ��ꎩ�g�̃p�����[�^�[�ɂ��ˑ����邽�߁A�p�����[�^�[�������t�B�b�g�����������I�����܂��B�ŏ��̃p�����[�^�[ $(\alpha_1,\rho_1,\sigma_1)$ �� 2m �����̃N�H�[�g�ɍ��킹�Ē�������A���̌�A�œK�l�ɌŒ肳��܂��B�����āA$(\alpha_2,\rho_2,\sigma_2)$ �͂Q�Ԗڂ̖����ɍ��킹�Ē�������܂��B���̃v���Z�X�́A�V�̂R�p�����[�^�[�L�����u���[�V�������̃V�[�P���X���I������܂ő������܂��F
| $($1$)$ |
���l����
��L�̃L�����u���[�V������� $(1)$ ���������߂ɁAnAG ���C�u��������A����`�ŏ������ɓ��������Q�̃\���o�[�������܂��F
- �����𗘗p����iderivative-based�j�\���o�[�F handle_solve_bxnl�ie04gg�j
- �����𗘗p���Ȃ��iderivative-free�j�\���o�[�F handle_solve_dfls�ie04ff�j
Heston ���f���̌����ȓ����͗��p�ł��Ȃ����߁Ae04gg ���K�v�Ƃ���c���̃��R�r�A�����A�L��������p���Đ��肵�܂��B�L�����������ʓI�Ɏg�p���邱�Ƃ͔��ɓ���A�����ł́A���l�����̌��ʁA���̐ۓ��p�����[�^�[ $h=10^{-6}$ ��I�т܂����B
��r�̂��߂ɁA�����̃\���o�[�ɑ��āA���������I�Ȓ�~����g���܂��B���Ȃ킿�A�t�B�b�g�́A1 �x�[�V�X�|�C���g���x�ɒB����Ηǂ����̂Ƃ݂Ȃ��܂��F
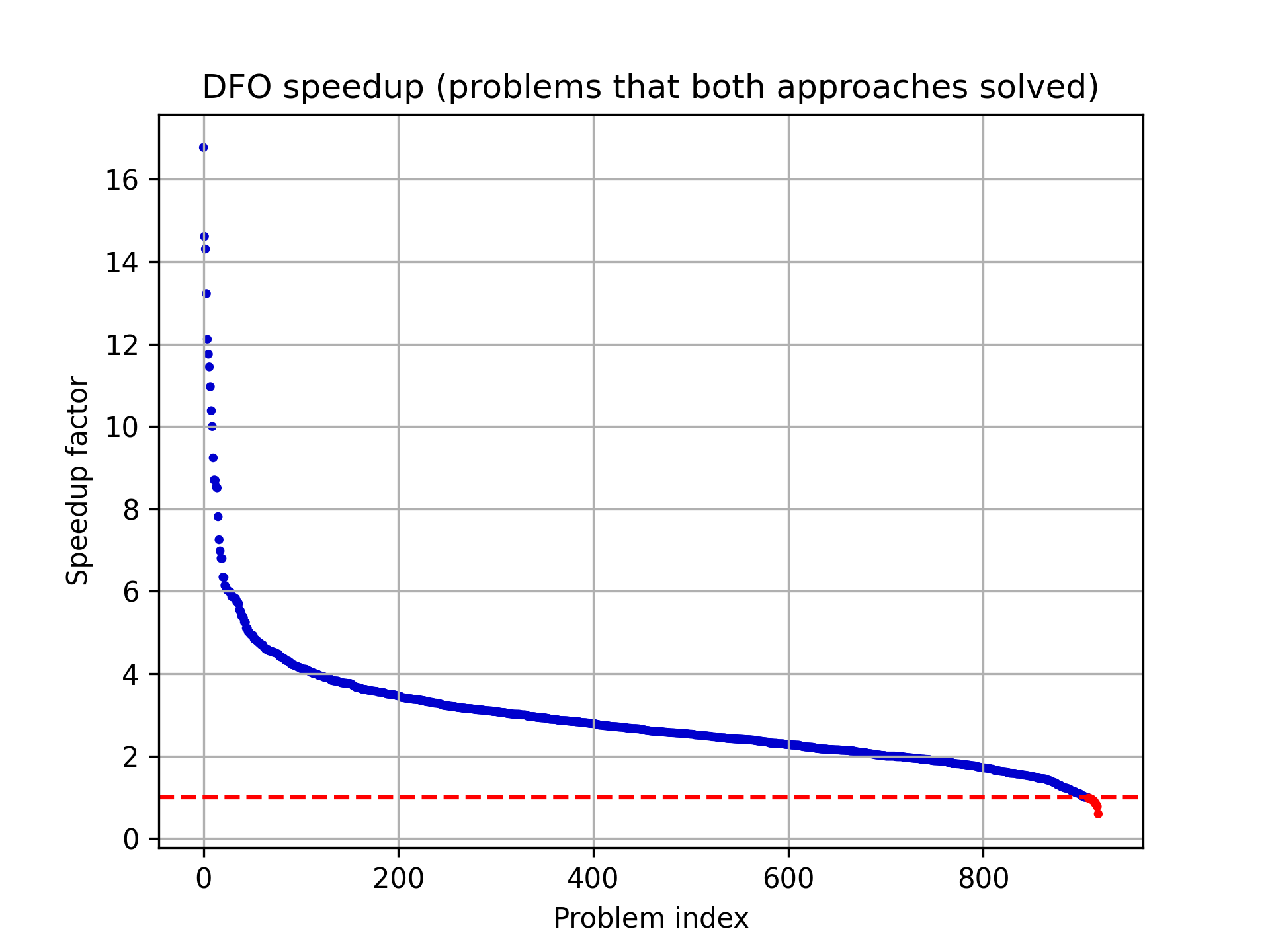
�g�p�����f�[�^�ɂ́A�����ׂ��V�̃L�����u���[�V�������� 1070 �̃V�[�P���X���`���� 1070 �̓��t���܂܂�Ă��܂��i���v 7490�j�B���ׂĂ𗼕��̃\���o�[�ʼn��������ʂ��܂Ƃ߂�ƁA���̂悤�ɂȂ�܂��F
-
Heston ���f���̑��Ăяo���F
- DFO�F258540�i���� 241�j�A���z�x�[�X�F 963933�i���� 900�j
- DFO �̕]���� 3.7 �{���Ȃ��B
-
�P�x�[�V�X�|�C���g�ɒB���Ȃ������L�����u���[�V�����̑����F
- DFO�F32�i20 ���j�A���z�x�[�X�F 180�i138 ���j
- DFO �� 98% �̖���v�����x�ʼn������̂ɑ��A���z�x�[�X�� 87% �ł����B
-
���\���o�[���������Ƃ��ł������ɑ��� Heston ���f���̌Ăяo���F
- DFO�F211326�i���� 229�j�A���z�x�[�X�F 575379�i���� 626�j
- DFO �� 2.7 �{���Ȃ��]���ōς݂܂����B
���}�́A���z�i�L�������j�x�[�X�̃\���o�[�ɑ��� DFO �\���o�[�̍��������A��肠����ɕK�v�Ȋ��]�����̔䗦�ŕ\�������̂ł��B���_�� DFO �\���o�[�̕��������ɉ��������\���A�Ԃ��_�͌��z�x�[�X�̃\���o�[�̕��������ɉ��������\���Ă��܂��B�قƂ�ǂ̖��ŁADFO �\���o�[�̕����������������Ƃ����Ď��܂��B
�d�v�ȃ|�C���g
�u���b�N�{�b�N�X���f���̃L�����u���[�V�����͎����Ȗ��ł͂Ȃ��̂ŁA�����̐��m�Ȑ��肪�ł��Ȃ��ꍇ�́A�����𗘗p���Ȃ��\���o�[�̎g�p����������K�v������܂��B��L�� Heston �L�����u���[�V�����̗�Ŏ������悤�ɁADFO �\���o�[���g���A��菭�Ȃ��Ăяo���ŁA���ǂ��t�B�b�g��������\���������ƌ����܂��B
�ߋ��̃u���O�� ������ ���������������B�܂��AGitHub Local optimization �y�[�W������l�X�ȗ�������邱�Ƃ��ł��܂��B
�Q�l����
[1] Coralia Cartis, Jan Fiala, Benjamin Marteau, and Lindon Roberts. Improving the exibility and robustness of model-based derivative-free optimization solvers. ACM Trans. Math. Softw., 45$($3$)$, August 2019.
