最適化問題の性質をより良く理解するために、以下の例を考えてみましょう:
\(f(x) = e^{x_1} (4x_1^2 + 2x_2^2 + 4x_1x_2 + 2x_2 + 1).\)
(この関数は、制約のない最適化ルーチンのドキュメントで例題関数として使用されています。)
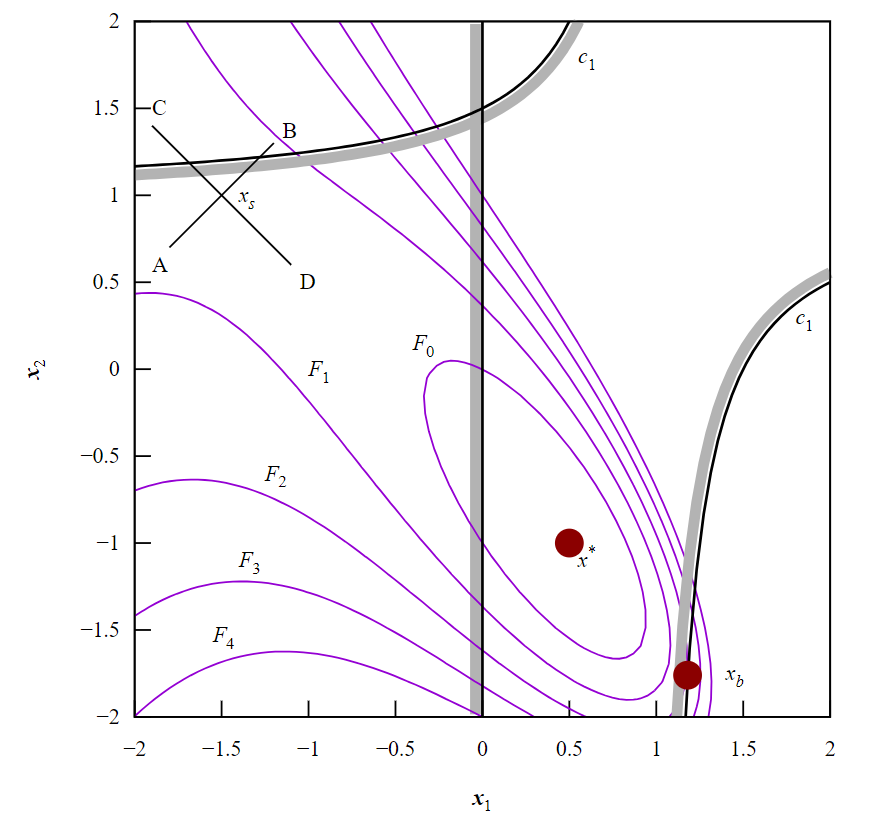
図1は\(f(x)\)の等高線図を示しています。\(F_0, F_1, \ldots, F_4\)とラベル付けされた等高線は、等値線または関数\(f(x)\)が特定の一定値をとる線です。点\(x^* = (\frac{1}{2}, -1)^T\)は局所無制約最小値です。つまり、\(f(x^*)\)の値(\(= 0\))は周囲のすべての点よりも小さくなっています。関数には複数のこのような最小値が存在する可能性があります。
点\(x_s\)は鞍点と呼ばれます。これは、線ABに沿っては最小値ですが、CDに沿っては最大値となるためです。
\(f(x)\)の最小化問題に制約\(x_1 \geq 0\)(単純な境界制約)を追加しても、解は変わりません。図1では、この制約は\(x_1 = 0\)を通る直線で表され、線上の影は許容されない領域(\(x_1 < 0\))を示しています。
非線形制約\(g_1(x) : x_1 + x_2 - x_1x_2 - \frac{3}{2} \geq 0\)を追加すると(図1の曲線の影付き線で表されています)、\(x^*\)は実行可能点ではなくなります。これは\(g_1(x^*) < 0\)となるためです。新しい制約付き問題の解は\(x_b \simeq (1.1825, -1.7397)^T\)となり、これは実行可能領域内で最小の関数値を持つ点です(ここで\(f(x_b) \simeq 3.0607\))。
