Keyword: 線形計画, スパース, 凸2次計画問題
概要
本サンプルは線形計画(スパース)及び凸2次計画問題を解くC#によるサンプルプログラムです。 本サンプルは以下に示される二次関数を最小化する解を求めて出力します。
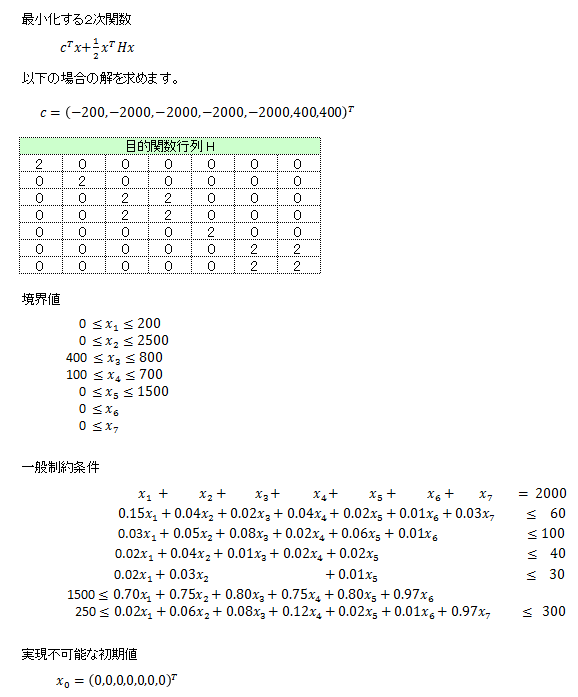
※本サンプルはnAG Library for .NETに含まれる関数 e04nk() のExampleコードです。本サンプル及び関数の詳細情報は e04nk のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はe04nk のマニュアルページを参照)| このデータをダウンロード |
e04nk Example Program Data
7 8 :Values of N and M
48 8 7 'C' 15 :Values of NNZ, IOBJ, NCOLH, START and NNAME
' ' ' ' ' ' ' ' ' ' :End of NAMES
'...X1...' '...X2...' '...X3...' '...X4...' '...X5...'
'...X6...' '...X7...' '..ROW1..' '..ROW2..' '..ROW3..'
'..ROW4..' '..ROW5..' '..ROW6..' '..ROW7..' '..COST..' :End of CRNAME
0.02 7 1
0.02 5 1
0.03 3 1
1.00 1 1
0.70 6 1
0.02 4 1
0.15 2 1
-200.00 8 1
0.06 7 2
0.75 6 2
0.03 5 2
0.04 4 2
0.05 3 2
0.04 2 2
1.00 1 2
-2000.00 8 2
0.02 2 3
1.00 1 3
0.01 4 3
0.08 3 3
0.08 7 3
0.80 6 3
-2000.00 8 3
1.00 1 4
0.12 7 4
0.02 3 4
0.02 4 4
0.75 6 4
0.04 2 4
-2000.00 8 4
0.01 5 5
0.80 6 5
0.02 7 5
1.00 1 5
0.02 2 5
0.06 3 5
0.02 4 5
-2000.00 8 5
1.00 1 6
0.01 2 6
0.01 3 6
0.97 6 6
0.01 7 6
400.00 8 6
0.97 7 7
0.03 2 7
1.00 1 7
400.00 8 7 :End of matrix A
0.0 0.0 4.0E+02 1.0E+02 0.0 0.0 0.0 2.0E+03
-1.0E+25 -1.0E+25 -1.0E+25 -1.0E+25 1.5E+03 2.5E+02 -1.0E+25 :End of BL
2.0E+02 2.5E+03 8.0E+02 7.0E+02 1.5E+03 1.0E+25 1.0E+25 2.0E+03
6.0E+01 1.0E+02 4.0E+01 3.0E+01 1.0E+25 3.0E+02 1.0E+25 :End of BU
0 0 0 0 0 0 0 0 :End of ISTATE
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 :End of XS
- 1行目はタイトル行で読み飛ばされます。
- 2行目に変数の数(n)、一般制約の数(m)を指定しています。
- 3行目の1番目のパラメータ(nnz)は線形制約行列の非ゼロ要素の数を指定しています。2番目のパラメータ(iobj)は線形目的項cTxのベクトルcの非ゼロ要素の行を指定しています。3番目のパラメータ(ncolh)はヘッセ行列の非ゼロカラムの数を指定しています。4番目のパラメータ(start)はどのように開始時の基底行列が得られるかを指定しています。"C"は初期の基底行列を選択するためにCrashプロシージャが使用されることを意味します。5番目のパラメータ(nname)は列と行の名前の数を指定しています。
- 4行目にいわゆるMPSX形式の問題に関する名前(names)を指定しています。
- 5〜7行目に列と行の名前(crname)を指定しています。
- 8〜55行目に線形制約行列の非ゼロ要素の値(a)、行のインデックス(ha)、列のインデックス(icol)を指定しています。
- 56〜57行目に変数の下限と制約の下限(bl)を指定しています。
- 58〜59行目に変数の上限と制約の上限(bu)を指定しています。
- 60行目に変数xの初期状態(istate)を指定しています。"0"は基底行列に適していることを意味します。
- 61行目に変数xの初期推定値(xs)を指定しています。
出力結果
(本関数の詳細はe04nk のマニュアルページを参照)| この出力例をダウンロード |
e04nk Example Program Results
Computed values of the size of z and iz are 358, 428 respectively.
Calls to E04NMF
---------------
List
Print level = 10
*** E04NKF
Parameters
----------
Frequencies.
Check frequency......... 60 Expand frequency........ 10000
Factorization frequency. 100
LP Parameters.
Scale tolerance......... 9.00E-01 Feasibility tolerance... 1.00E-06
Iteration limit......... 75 Scale option............ 2
Optimality tolerance.... 1.00E-06 Partial price........... 10
Crash tolerance......... 1.00E-01 Pivot tolerance......... 2.04E-11
Crash option............ 2
QP objective.
Objective variables..... 7 Hessian columns......... 7
Superbasics limit....... 7
Miscellaneous.
Variables............... 7 Linear constraints...... 8
LU factor tolerance..... 1.00E+02 LU update tolerance..... 1.00E+01
LU singularity tolerance 2.04E-11 Monitoring file......... -1
EPS (machine precision). 1.11E-16 Print level............. 10
Infinite bound size..... 1.00E+20 Infinite step size...... 1.00E+20
COLD start.............. MINIMIZE................
Workspace provided is IZ( 428), Z( 358).
To start solving the problem we need IZ( 428), Z( 358).
Itn Step Ninf Sinf/Objective Norm rg
Itn 0 -- Infeasible.
0 0.0E+00 1 1.152891E+03 0.0E+00
1 4.3E+02 0 0.000000E+00 0.0E+00
Itn 1 -- Feasible point found (for 1 equality constraints).
1 0.0E+00 0 0.000000E+00 0.0E+00
1 0.0E+00 0 1.460000E+06 0.0E+00
Itn 1 -- Feasible QP solution.
2 8.7E-02 0 9.409959E+05 0.0E+00
3 5.3E-01 0 -1.056552E+06 0.0E+00
4 1.0E+00 0 -1.462190E+06 0.0E+00
5 1.0E+00 0 -1.698092E+06 1.8E-12
6 4.6E-02 0 -1.764906E+06 7.0E+02
7 1.0E+00 0 -1.811946E+06 1.4E-12
8 1.7E-02 0 -1.847325E+06 1.7E+02
9 1.0E+00 0 -1.847785E+06 9.1E-13
Variable State Value Lower Bound Upper Bound Lagr Mult Residual
...X1... LL 0.00000 . 200.00 2361. .
...X2... BS 349.399 . 2500.0 -1.2975E-12 349.4
...X3... SBS 648.853 400.00 800.00 -5.7329E-13 151.1
...X4... SBS 172.847 100.00 700.00 6.4970E-13 72.85
...X5... BS 407.521 . 1500.0 9.1881E-13 407.5
...X6... BS 271.356 . None -1.1928E-12 271.4
...X7... BS 150.023 . None -1.4130E-12 150.0
Constrnt State Value Lower Bound Upper Bound Lagr Mult Residual
..ROW1.. EQ 2000.00 2000.0 2000.0 -1.2901E+04 .
..ROW2.. BS 49.2316 None 60.000 . -10.77
..ROW3.. UL 100.000 None 100.00 -2325. .
..ROW4.. BS 32.0719 None 40.000 . -7.928
..ROW5.. BS 14.5572 None 30.000 . -15.44
..ROW6.. LL 1500.00 1500.0 None 1.4455E+04 .
..ROW7.. LL 250.000 250.00 300.00 1.4581E+04 .
..COST.. BS -2.988690E+06 None None -1.000 -2.9887E+06
Exit E04NKF - Optimal QP solution found.
Final QP objective value = -1847785.
Exit from QP problem after 9 iterations.
** e04nk returned with ifail = 0
Variable Istate Value Lagr Mult
...X1... 0 0 2361
...X2... 3 349.399 -1.298e-12
...X3... 2 648.853 -5.733e-13
...X4... 2 172.847 6.497e-13
...X5... 3 407.521 9.188e-13
...X6... 3 271.356 -1.193e-12
...X7... 3 150.023 -1.413e-12
Constrnt Istate Value Lagr Mult
..ROW1.. 0 2000 -1.29e+04
..ROW2.. 3 49.2316 0
..ROW3.. 1 100 -2325
..ROW4.. 3 32.0719 0
..ROW5.. 3 14.5572 0
..ROW6.. 0 1500 1.445e+04
..ROW7.. 0 250 1.458e+04
..COST.. 3 -2.98869e+06 -1
Final objective value = -1847785
- 2行目に作業域である z と iz のサイズの計算値がそれぞれ 358 と 428 であることが示されています。
- 9行目にPrint Level に"10"が設定されていることが示されています。
- 16〜37行目に以下に示すプログラムのオプション引数が出力されています。
Check frequency 因数分解後にこの回数の反復ごとに現在の解が一般線形制約を満たしているかを確認するための数値テストが行われます。 Expand frequencey この反復数を超えると実行可能許容値が増加します。 Factorization Frequency 最大でこの回数の基底変換が基底行列の因数分解で生じます。 Scale tolerance スケーリングパスの数を制御します。 Feasibility tolerance 実行可能点での各制約の許容可能な最大の絶対的違反。 Iteration limit 最大反復数。 Scale option 変数と制約のスケーリング。"2"は付加的なスケーリングが実行されることを意味しています。 Optimality tolerance 縮小勾配の大きさの判断に使用されます。 Partial price プライシングに必要な処理を軽減します。 Crash tolerance Crash処理で三角基底の検索時に行列Aの非ゼロ要素を無視できるようにします。 Pivot tolerance カラムが基底行列に入ることで基底行列が特異行列になるのを防ぐために使用されます。 Crash option 制約行列Aのどの行や列が基底に値するかを決定し、Crash処理が何回呼び出されるかを示します。 Objective variables 目的関数の数。 Hessian columns ヘッセ行列のカラム数。 Superbasics limit superbasic 変数の上限。 Variables 変数の数。 Linear constraints 線形制約の数。 LU factor tolerance 再因数分解時の基底因数分解の安定性及びスパース性を制御します。 LU update tolerance 更新時の基底因数分解の安定性及びスパース性を制御します。 LU singularity tolerance 悪条件の基底行列を防ぐために使用される特異点許容値。 Monitoring file モニタリング情報をファイルに送信するかモニタリング情報を生成しないかを示しています。"-1"はモニタリング情報を生成しないことを意味します。 EPS (machine precision) マシン精度。 Print level 出力レベル。"10"は最終的な解と各反復ごとのサマリーを出力することを意味します。 Infinite bound size 問題の制約における無限境界。 Infinite step size 無限解へのステップと見なされる変数の変化の大きさ。 COLD start プログラムが COLD startであることを示しています。初期の基底行列を選択するため Crash処理が使用されます。 MINIMIZE 最適化の方向が最小化であることを示しています。 - 39行目は与えられている作業域である IZ と Z のサイズが出力されています。
- 40行目は問題を解くために必要な IZ と Z のサイズが出力されています。
- 43〜58行目には以下が出力されています。
Itn 反復回数。 Step 探索方向に進んだステップの長さ。 Ninf 違反した制約の数。 Sinf/Objective xが実行可能でない場合は制約違反の大きさの合計。実行可能な場合は目的関数の値。 Norm rg 縮小勾配のユークリッドノルム。 - 61〜69行目には以下が出力されています。
Variable 変数の名前。 State 変数の状態(LLは下限での非基底、SBSはsuperbasic、BSは基底であることを意味します)。 Value 最後の反復の変数の値。 Lower Bound 下限。 Upper Bound 上限。 Lagr Mult 関連する境界のラグランジュ乗数。 Residual 残差(変数の値と上限/下限の近いほうとの差)。 - 72〜81行目には以下が出力されています。
Constrnt 線形制約の名前。 State 線形制約の状態(ULは上限での非基底、LLは下限での非基底、EQは非基底で固定、BSは基底であることを意味します)。 Value 最後の反復の制約の値。 Lower Bound 下限。 Upper Bound 上限。 Lagr Mult 関連する境界のラグランジュ乗数。 Residual 残差(制約の値と上限/下限の近いほうとの差)。 - 83行目に最適解が見つかったことが示されています。
- 85行目に最終的な目的関数値が出力されています。
- 87行目にはQP問題を解くのに9回の反復が行われたことが示されています。
- 91〜99行目に変数の名前、変数の状態、変数の値、ラグランジュ乗数が出力されています。
- 102〜111行目に線形制約の名前、線形制約の状態、制約の値、ラグランジュ乗数が出力されています。
- 114行目に最終的な目的関数値が出力されています。
ソースコード
(本関数の詳細はe04nk のマニュアルページを参照)
※本サンプルソースコードは .NET環境用の科学技術・統計計算ライブラリである「nAG Library for .NET」の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
// e04nk Example Program Text
// C# version, nAG Copyright 2008
using System;
using NagLibrary;
using System.IO;
namespace NagDotNetExamples
{
public class E04NKE
{
static bool defaultdata = true;
static string datafile = "";
// as a command line argument. It defaults to the named file specified below otherwise.
//
static void Main(String[] args)
{
if (args.Length == 1)
{
defaultdata = false;
datafile = args[0];
}
StartExample();
}
public static void StartExample()
{
E04.E04NK_QPHX qphxE04NK = new E04.E04NK_QPHX(qphx);
try
{
DataReader sr = null;
if(defaultdata)
{ sr = new DataReader("exampledata/e04nke.d");
}
else
{
sr = new DataReader(datafile);
}
double obj, sinf;
int i, icol=0, ifail, iobj, j, jcol, m, miniz, minz, n, ncolh, ninf, nname, nnz, ns=0;
string start = "";
int idummy = -11111;
int nmax = 100;
int mmax = 100;
int nnzmax = 100;
string[] names = new string[5];
Console.WriteLine("e04nk Example Program Results");
// Skip heading in data file.
sr.Reset();
sr.Reset();
n = int.Parse(sr.Next());
m = int.Parse(sr.Next());
//
// Read nnz, iobj, ncolh, start and nname from data file.
//
sr.Reset();
nnz = int.Parse(sr.Next());
iobj = int.Parse(sr.Next());
ncolh = int.Parse(sr.Next());
start = sr.Next();
nname = int.Parse(sr.Next());
//
// Read names and crname from data file.
//
double[] a = new double[nnz];
double[] bl = new double[n + m];
double[] bu = new double[n + m];
double[] clamda = new double[n + m];
double[] xs = new double[n + m];
int[] ha = new int[nnz];
int[] istate = new int[n + m];
int[] ka = new int[n + 1];
string[] crname = new string[n + m];
sr.Reset();
for (i = 1; i <= 5; i++)
{
names[i - 1] = sr.Next();
}
sr.Reset();
for (i = 1; i <= nname; i++)
{
crname[i - 1] = sr.Next();
}
//
// read the matrix a from data file. Set up ka.
//
jcol = 1;
ka[jcol - 1] = 1;
for (i = 1; i <= nnz; i++)
{
//
// Element ( ha( i-1 ), icol ) is stored in a[ i-1].
//
sr.Reset();
a[i - 1] = double.Parse(sr.Next());
ha[i - 1] = int.Parse(sr.Next());
icol = int.Parse(sr.Next());
//
if (icol < jcol)
{
//
// Elements not ordered by increasing column index.
//
Console.WriteLine("\n {0}{1,5}{2}{3,5}{4}{5}", "Element in column", icol, " found after element in column", jcol, ". Problem", " abandoned.");
goto L120;
}
else if (icol == jcol + 1)
{
//
// Index in a of the start of the icol-th column equals I.
//
ka[icol - 1] = i;
jcol = (int)icol;
}
else if (icol > jcol + 1)
{
//
// Index in a of the start of the icol-th column equals i,
// but columns jcol+1,jcol+2,...,icol-1 are empty. Set the
// corresponding elements of ka to i.
//
for (j = jcol + 1; j <= icol - 1; j++)
{
ka[j - 1] = i;
}
ka[icol - 1] = i;
jcol = (int)icol;
}
}
//
ka[n + 1 - 1] = nnz + 1;
//
if (n > icol)
{
//
// Columns n,n-1,...,icol+1 are empty. Set the corresponding
// elements of ka accordingly.
//
for (i = n; i <= icol + 1; i += -1)
{
if (ka[i - 1] == idummy)
{
ka[i - 1] = ka[i + 1 - 1];
}
}
}
//
// Read bl, bu, istate and xs from data file.
//
sr.Reset();
for (i = 1; i <= n + m; i++)
{
bl[i - 1] = double.Parse(sr.Next());
}
sr.Reset();
for (i = 1; i <= n + m; i++)
{
bu[i - 1] = double.Parse(sr.Next());
}
if (start == "C")
{
sr.Reset();
for (i = 1; i <= n; i++)
{
istate[i - 1] = int.Parse(sr.Next());
}
}
else if (start == "W")
{
sr.Reset();
for (i = 1; i <= n + m; i++)
{
istate[i - 1] = int.Parse(sr.Next());
}
}
sr.Reset();
for (i = 1; i <= n; i++)
{
xs[i - 1] = double.Parse(sr.Next());
}
//
// Initialise E04.e04nk
//
// Switch off all output.
PrintManager.Warning = new PrintManager.MessageLogger(discardmessage);
PrintManager.Message = new PrintManager.MessageLogger(discardmessage);
E04.e04nkOptions options = new E04.e04nkOptions();
//
// Solve the QP problem.
//
//
start = "C";
// First get appropriate minimum lengths of arrays, z and iz
int lenz = 1;
int leniz = 1;
double[] z = new double[lenz];
int[] iz = new int[leniz];
E04.e04nk(n, m, nnz, iobj, ncolh, qphxE04NK, a, ha, ka, bl, bu,
start, names, nname, crname, ref ns, xs, istate, out miniz,
out minz, out ninf, out sinf, out obj, clamda, iz, z, options, out ifail);
Console.WriteLine("Computed values of the size of z and iz are {0}, {1} respectively.", minz, miniz);
lenz = 358;
leniz = 428;
z = new double[lenz];
iz = new int[leniz];
// Initialise E04.e04nk again and check for error exits
PrintManager.Warning = new PrintManager.MessageLogger(printmessage);
PrintManager.Message = new PrintManager.MessageLogger(printmessage);
options = new E04.e04nkOptions();
options.Set("List");
options.Set("Print level = 10");
E04.e04nk(n, m, nnz, iobj, ncolh, qphxE04NK, a, ha, ka, bl, bu,
start, names, nname, crname, ref ns, xs, istate, out miniz,
out minz, out ninf, out sinf, out obj, clamda, iz, z, options, out ifail);
//
// Check for error exits
//
Console.WriteLine("");
if (ifail == 7)
{
Console.WriteLine(" ** An input parameter is invalid");
}
else if (ifail >= 0)
{
Console.WriteLine(" ** e04nk returned with ifail = {0, 3}", ifail);
Console.WriteLine("");
Console.WriteLine(" Variable Istate Value Lagr Mult");
Console.WriteLine("");
for (i = 1; i <= n; i++)
{
Console.WriteLine(" {0} {1,3} {2,14:g6} {3,12:g4}", crname[i - 1], istate[i - 1], xs[i - 1], clamda[i - 1]);
}
if (m > 0)
{
//
Console.WriteLine("");
Console.WriteLine("");
Console.WriteLine(" Constrnt Istate Value Lagr Mult");
Console.WriteLine("");
for (i = n + 1; i <= n + m; i++)
{
j = i - n;
Console.WriteLine(" {0} {1,3} {2,14:g6} {3,12:g4}", crname[i - 1], istate[i - 1], xs[i - 1], clamda[i - 1]);
}
}
Console.WriteLine("");
Console.WriteLine("");
Console.WriteLine(" Final objective value = {0,15:g7}", obj);
}
else
{
Console.WriteLine(" ** e04nk returned with ifail = {0, 3}", ifail);
}
L120: ;
//
}
catch (Exception e)
{
Console.WriteLine(e.Message);
Console.WriteLine( "Exception Raised");
}
}
//
public static void qphx(int nstate, int ncolh, double[] x, double[] hx)
{
//
// Routine to compute H*x. (In this version of QPHX, the Hessian
// matrix h is not referenced explicitly.)
//
double two = 2.00e+0;
hx[0] = two * x[0];
hx[1] = two * x[1];
hx[2] = two * (x[2] + x[3]);
hx[3] = hx[2];
hx[4] = two * x[4];
hx[5] = two * (x[5] + x[6]);
hx[6] = hx[5];
//
}
static void discardmessage(String message)
{
}
static void printmessage(String message)
{
Console.WriteLine(message);
}
}
}
