Keyword: 大域的最適化
概要
本サンプルは大域的最適化を行うC#によるサンプルプログラムです。 本サンプルは以下に示される2次元におけるpeaks関数の大域的最小値を求めて出力します。
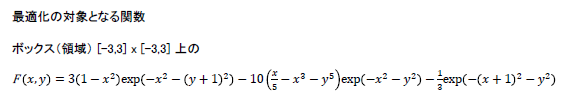
※本サンプルはnAG Library for .NETに含まれる関数 e05jb() のExampleコードです。本サンプル及び関数の詳細情報は e05jb のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はe05jb のマニュアルページを参照)| このデータをダウンロード |
e05jc Example Program Data 3 : SDLIST 0 : IBOUND -3.0 -3.0 : Lower bounds BL 3.0 3.0 : Upper bounds BU 3 : IINIT 3 3 3 : NUMPTS -3.0 -1.0 3.0 -3.0 0.0 3.0 : Matrix LIST 2 2 2 : INITPT F : LPLOT Begin example options file * Comment lines like this begin with an asterisk * Set the maximum number of function evaluations Function Evaluations Limit = 100000 * Set the local search termination tolerance Local Searches Tolerance = 1.0D-10 * Set the maximum number of times a given box may be split Splits Limit = 20 End
- 1行目はタイトル行で読み飛ばされます。
- 2行目に初期化リストに従って分割が行われる座標の点の数の最大値(sdlist)を指定しています。
- 3行目には境界値を処理するための機能が使用されるかを示すパラメータ(ibound)指定しています。"0"は下限と上限をそれぞれ与えることを意味します。
- 4行目には下限(bl)を指定しています。
- 5行目には上限(bu)を指定しています。
- 6行目にはどの初期化の手法が使用されるかを示すパラメータ(IINIT)指定しています。"3"はユーザが初期化リストを提供することを意味しています。
- 7行目には分割が行われる座標の点の数(numpts)を指定しています。
- 8行目には初期化リスト(list)を指定しています。
- 9行目には関数が初期の座標点と見なすようなリスト上の点(initpt)を指定しています。
- 10行目に最新の検索ボックス(領域)の情報を表示するかどうかを示すパラメータ(lplot)を指定しています。"F"は表示しないことを意味します。
- 11〜19行目には以下に示すオプション・パラメータを設定するオプションファイルを定義しています。
Function Evaluations Limit 関数の呼び出し回数の近似限界。 Local Searches Tolerance 近似勾配が小さい場合に停止する基準として局所探索の際に使用される乗数。 Splits Limit ボックス(領域)の分割回数の限界。
出力結果
(本関数の詳細はe05jb のマニュアルページを参照)| この出力例をダウンロード |
e05jb Example Program Results (OBJFUN was just called for the first time) *** Begin monitoring information *** Total sub-boxes = 180 Total function evaluations = 186 Total function evaluations used in local search = 103 Total points used in local search = 9 Total sweeps through levels = 9 Total splits by init. list = 5 Lowest level with nonsplit boxes = 6 Number of candidate minima in the "shopping basket" = 2 Shopping basket: xbaskt( 1,:) = 0.22828 -1.34740 xbaskt( 2,:) = -1.62553 0.20452 *** End monitoring information *** On exit from e05jb, ifail = 0 Final objective value = -6.55113 Global optimum x = 0.22828 -1.62553
- 8〜18行目に以下に示すモニタリング情報が出力されています。
- サブボックス(下位領域)の数
- 関数objfunの呼び出しの累積数
- 局所検索での関数objfunの呼び出しの累積数
- 局所検索の開始点として使用される座標点の数
- 分割のレベルを通じたスイープ(sweep)の累積数
- 初期化リストによる分割の累積数
- 分割していないボックス(領域)を含む、最も低い分割のレベル
- ショッピングバスケット(最小値の候補の格納場所)の最小値の候補の座標点の数
- 最小値の候補が格納されているショッピングバスケットの内容
- 23行目にエラーを検知せずに本関数 e05jb を終了したことを示しています。
- 24行目に最終的な関数値が出力されています。
- 25行目に大域的最適解xの値が出力されています。
ソースコード
(本関数の詳細はe05jb のマニュアルページを参照)
※本サンプルソースコードは .NET環境用の科学技術・統計計算ライブラリである「nAG Library for .NET」の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
// e05jb Example Program Text
//
// C# version, nAG Copyright 2008
using System;
using NagLibrary;
namespace NagDotNetExamples
{
public class E05JBE
{
const int n=2;
static bool defaultdata = true;
static string datafile = "";
static bool lplot;
static void Main(String[] args)
{
if (args.Length == 1)
{
defaultdata = false;
datafile = args[0];
}
StartExample();
}
public static void StartExample()
{
try
{
DataReader sr = null;
if (defaultdata)
{
sr = new DataReader("exampledata/e05jbe.d");
}
else
{
sr = new DataReader(datafile);
}
// values of optional parameters associated with e05jb
//
double infbnd, obj; int i, ibound, iinit, j, sdlist, stclim;
string lcsrch="";
E05.E05JB_OBJFUN objfunE05JB = new E05.E05JB_OBJFUN(objfun);
E05.E05JB_MONIT monitE05JB = new E05.E05JB_MONIT(monit);
//
int ifail=0;
Console.WriteLine("e05jb Example Program Results");
//
// Skip heading in data file
//
sr.Reset();
//
// Read sdlist from data file
//
sr.Reset();
sdlist = int.Parse(sr.Next());
double[] bl = new double[n];
double[] bu = new double[n];
double[,] list = new double[n, sdlist];
double[] ruser = new double[1];
double[] x = new double[n];
int[] initpt = new int[n];
int[] numpts = new int[n];
//
//
// Read ibound, bl, and bu from data file
//
sr.Reset();
ibound = int.Parse(sr.Next());
//
if (ibound == 0)
{
//
// Read in the whole of each bound
//
sr.Reset();
for (i = 1 ; i <= n ; i++)
{
bl[i - 1] = double.Parse(sr.Next());
}
sr.Reset();
for (i = 1 ; i <= n ; i++)
{
bu[i - 1] = double.Parse(sr.Next());
}
//
}
else if (ibound == 3)
{
//
// Bounds are uniform: read in only the first entry of each
//
sr.Reset();
bl[0] = double.Parse(sr.Next());
sr.Reset();
bu[0] = double.Parse(sr.Next());
//
}
//
// Read in iinit (and list, numpts and initpt if necessary)
// from data file
//
sr.Reset();
iinit = int.Parse(sr.Next());
//
if (iinit == 3)
{
//
// User is specifying the initialization list
//
sr.Reset();
for (i = 1 ; i <= n ; i++)
{
numpts[i - 1] = int.Parse(sr.Next());
}
sr.Reset();
for (i = 1 ; i <= n ; i++)
{
for (j = 1 ; j <= numpts[i - 1] ; j++)
{
list[i - 1 , j - 1] = double.Parse(sr.Next());
}
}
sr.Reset();
for (i = 1 ; i <= n ; i++)
{
initpt[i - 1] = int.Parse(sr.Next());
}
//
}
//
// Read lplot. Its value determines whether monit displays
// information on the current search box
//
sr.Reset();
lplot = bool.Parse(sr.Next());
//
// Initialize e05jb
//
E05.e05jbOptions options = new E05.e05jbOptions();
//
if (ifail >= 0)
{
//
// Use e05jb to read some options from the end of the data
// file
//
options.Set(sr);
Console.WriteLine("");
//
// Set 'Static Limit'
//
stclim = 4 * n;
options.Set("Static Limit", stclim);
//
// Set 'Infinite Bound Size' tenfold
//
infbnd = 1.00e100;
options.Set("Infinite Bound Size", infbnd);
//
// Set the option 'Local Searches Limit = 40'
//
options.Set("Local Searches Limit = 40");
//
// Set the option 'Local Searches' to 'On'
//
lcsrch = "On";
options.Set("Local Searches", lcsrch);
//
// Solve the problem.
//
E05.e05jb(n, objfunE05JB, ibound, iinit, bl, bu, list, numpts, initpt, monitE05JB, x,
out obj,
options, out ifail);
//
Console.WriteLine("");
if (ifail >= 0)
{
Console.WriteLine(" On exit from e05jb, ifail ={0,5}",ifail);
//
if (ifail == 0)
{
Console.WriteLine(" Final objective value ={0,11:f5}",obj);
Console.Write("Global optimum x = ");
for (i = 1 ; i <= n ; i++)
{
Console.Write(" {0, 9:f5}", x[i - 1]);
}
Console.WriteLine();
}
}
else
{
Console.WriteLine(" ** e05jb returned with ifail = {0, 3}", ifail);
}
//
}
//
//
}
catch (Exception e)
{
Console.WriteLine(e.Message);
Console.WriteLine("Exception Raised");
}
}
//
public static void objfun (int n, double[] x, out double f, int nstate,
out int inform)
{
//
// Routine to evaluate objective function.
//
double x1, x2;
//
inform = 0;
f = 0.0;
if ((inform) >= 0)
{
//
// If inform >= 0 then we're prepared to evaluate objfun
// at the current x
//
if (nstate == 1)
{
//
// This is the first call to objfun
//
Console.WriteLine("");
Console.WriteLine(" (OBJFUN was just called for the first time)");
}
//
x1 = x[0];
x2 = x[1];
//
f = 3.0e0*(1.0e0-x1)*(1.0e0-x1)*Math.Exp(-(x1*x1)-(x2+1)*(x2+1)) -
1.0e1*(x1/5.0e0-Math.Pow(x1, 3)-Math.Pow(x2,5))*Math.Exp(-x1*x1-x2*x2) -
1.0e0/3.0e0*Math.Exp(-(x1+1.0e0)*(x1+1.0e0)-x2*x2);
}
//
//
}
//
public static void monit (int n, int ncall, double[] xbest, int[] icount,
double[,] list, int[] numpts, int[] initpt, int nbaskt, double[,] xbaskt,
double[] boxl, double[] boxu, int nstate, out int inform)
{
//
// Monitoring method.
//
int i, j; // inform;
//
inform = 0;
if ((inform) >= 0)
{
//
// We are going to allow the iterations to continue.
// Extract plot from the integer communication-array
//
//
if ((nstate == 0) || (nstate == 1))
{
//
// When nstate == 1, monit is called for the first time. When
// nstate == 0, monit is called for the first AND last time.
// Display a welcome message
//
Console.WriteLine("");
Console.WriteLine(" *** Begin monitoring information ***");
Console.WriteLine("");
//
if (lplot && n == 2)
{
Console.WriteLine(" <Begin displaying search boxes>");
Console.WriteLine("");
}
//
}
//
if (lplot && n == 2)
{
//
// Display the coordinates of the edges of the current search
// box
//
outbox(ref n, boxl, boxu);
//
}
//
if (nstate <= 0)
{
//
// monit is called for the last time
//
if (lplot && n == 2)
{
Console.WriteLine(" <End displaying search boxes>");
Console.WriteLine("");
}
//
Console.WriteLine(" Total sub-boxes ={0,5}",icount[0]);
Console.WriteLine(" Total function evaluations ={0,5}",ncall);
Console.WriteLine(" Total function evaluations used in local search ={0,5}",icount[1]);
Console.WriteLine(" Total points used in local search ={0,5}",icount[2]);
Console.WriteLine(" Total sweeps through levels ={0,5}",icount[3]);
Console.WriteLine(" Total splits by init. list ={0,5}",icount[4]);
Console.WriteLine(" Lowest level with nonsplit boxes ={0,5}",icount[5]);
Console.WriteLine(" Number of candidate minima in the \"shopping basket\" ={0,5}",nbaskt);
Console.WriteLine(" Shopping basket:");
//
for (i = 1 ; i <= n ; i++)
{
Console.Write("xbaskt({0,3},:) = ", i);
for (j = 1 ; j <= nbaskt ; j++)
{
Console.Write(" {0, 9:f5}", xbaskt[i - 1 , j - 1]);
}
Console.WriteLine();
}
//
Console.WriteLine("");
Console.WriteLine(" *** End monitoring information ***");
Console.WriteLine("");
}
//
}
//
//
}
public static void outbox (ref int n, double[] boxl, double[] boxu)
{
//
// Displays edges of box with bounds boxl and boxu in format suitable
// for plotting.
//
//
//
Console.WriteLine("{0,20:f15} {1,20:f15}",boxl[0],boxl[1]);
Console.WriteLine("{0,20:f15} {1,20:f15}",boxl[0],boxu[1]);
Console.WriteLine("");
Console.WriteLine("{0,20:f15} {1,20:f15}",boxl[0],boxl[1]);
Console.WriteLine("{0,20:f15} {1,20:f15}",boxu[0],boxl[1]);
Console.WriteLine("");
Console.WriteLine("{0,20:f15} {1,20:f15}",boxl[0],boxu[1]);
Console.WriteLine("{0,20:f15} {1,20:f15}",boxu[0],boxu[1]);
Console.WriteLine("");
Console.WriteLine("{0,20:f15} {1,20:f15}",boxu[0],boxl[1]);
Console.WriteLine("{0,20:f15} {1,20:f15}",boxu[0],boxu[1]);
Console.WriteLine("");
//
//
}
}
}
