nAG ツールボックスにより nAG ライブラリの全機能が MATLAB® から使えるようになります。 MATLAB® を介して nAG をコールする利点は多くの引数の指定がオプショナル、あるいは不要になることで、 これによってコードを読みやすく保守しやすいものにすることができます。
それに加え、nAG ライブラリのすべてのドキュメント(印刷物だと 17 冊、本棚でかなりの幅を取ります) は MATLAB® ヘルプ形式に変換されているため、 MATLAB® からのアクセスは容易に行えます。 それぞれの nAG ライブラリ関数に対する記述の中には、 それの用法を示す MATLAB® コードの例が含まれています。
nAG ツールボックスの内容のいくつかについては既に
nAG Toolbox for MATLAB® 製品の使用例 - Part 1
でご紹介しています。ここでもその続きとして他の nAG を例に取り、
その用法、及び結果を MATLAB® のプロット機能で表示させる方法について説明します。
- Part 2 に引き続き Part 3 はこちらからご参照いただけます。
The C05 chapter - Finding the root of an equation
方程式の根の探索
まず連続関数のゼロ点の計算から見て行くことにします。C05 章にはそのための関数がいくつか 含まれています(その他に複数の未知数によって記述された非線形の連立方程式の解を求める関数もあります)。 最初の例では次の 2 次方程式の根を求めてみます。
25x^2 - 10x + 1 = 0
もちろんこの場合、x = 0.2 が重根であることは解析的に容易に確認できますが(以下に示すように 数値解のチェックに役立ちます)、C05 の各種関数は任意の関数(ただし連続であるとします) のゼロ点を求める上で使用できます。ここでは c05ax という関数を使用します。これは関数を 逆通信(reverse communication)を介して評価するもので、解探索途上における中間的な結果を 表示させることができます。
いくつかのプロットコマンドを含むコードを次に示します。
% Specify the function as a MATLAB anonymous function - this facilitates % changing the function for other examples. myfun = @(x)25*x*x - 10*x + 1; % Specify the initial estimate of the zero, and the value of the function % there (the latter is only needed for plotting). xstart = 1.0; fstart = myfun(xstart); xx = xstart; fx = fstart; % Specify other parameters for the nAG routine. tol is the tolerance, % used by the routine to control the accuracy of the solution. tol = 0.00001; ir = int32(0); c = zeros(26, 1); ind = int32(1); % Iterate until the solution is reached. while (ind ~= int32(0)) % Call the nAG routine to get an improved estimate of the zero, % then plot it. [xx, c, ind, ifail] = c05ax(xx, fx, tol, ir, c, ind); fx = myfun(xx); plot(xx, fx, 'or', 'MarkerFaceColor', [1,0,0], 'MarkerSize', 8); end % Plot initial estimate, and final solution. plot(axes, xstart, fstart, 'og', 'MarkerFaceColor', [0,1,0], 'MarkerSize', 8); plot(axes, xx, fx, 'oy', 'MarkerFaceColor', [1,1,0], 'MarkerSize', 8);
結果は次のグラフに示すようなものになります。
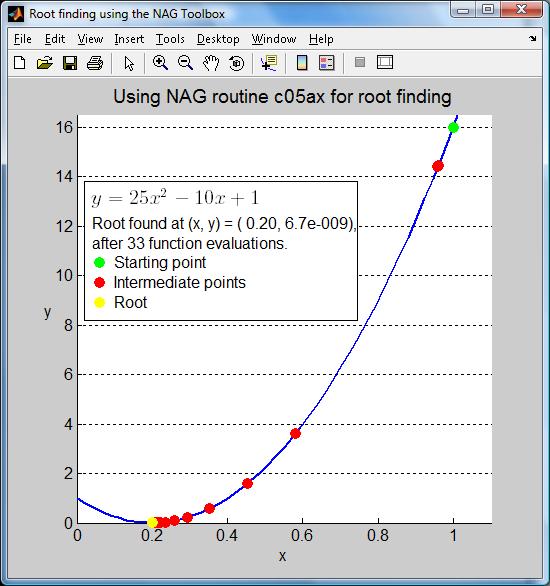
Figure 1: 2次式の根の探索
2 番目の例として、上に示したコードの最初の数行を変更し、 異なる関数(例えば解析的に求めるのが困難な関数)の根を探索してみます。 コードは次の通りです。
% Specify the function as a MATLAB anonymous function - this facilitates % changing the function for other examples. myfun = @(x)x - exp(-x); % Specify the initial estimate of the zero, and the value of the function % there (the latter is only needed for plotting). xstart = 5.0;
結果は figure 2 に示したようなものになります。
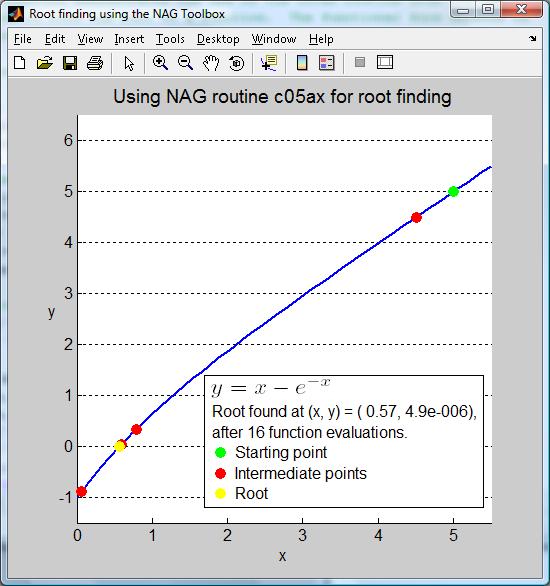
Figure 2: 超越関数の根の探索
The E02 Chapter - Fitting a set of points with a cubic spline
3次スプライン曲線のフィット
多くの科学分野において、一群のデータ点を近似する関数形を見つけることがしばしば必要になります。 データには通常測定誤差等のランダムな擾乱が含まれているため、それらを平滑化し除去した方が良い 場合が良くあります。 前回の記事では x-y 平面内の格子点上で与えられた一群の2次元データ値に対し、 nAG ツールボックスを用いて双 3 次スプライン近似を計算する例を示しました。結果は f(x,y) という形の 曲面だったわけです。ここでは 1 次元のケースについて見てみましょう。すなわち x 軸上で与えられたデ ータ点に対し、それらを近似する 3 次スプライン曲線 f(x) を求めます。そのための nAG 関数は e02be ですが、補助的な関数 e02bb を使用すると e02be の計算結果に基づき、任意の点におけるスプライン の値を計算することができます。
2 次元の場合と同様、フィットの適合度とスムーズさをバランスさせるためのパラメータを指定します。 e02be 中では s という名称のついた平滑化パラメータは、 その値が小さいほどデータへのフィットが完全に近いものとなります。 しかしここで言う“小さい”という表現の意味はそれぞれのデータセットごとに異なります。 極端な場合として s = 0 とした場合には、補間スプライン曲線が得られることになります。 一方、s として非常に大きな値を指定した場合には重み付きの最小 2 乗 3 次多項式近似を得ることができます。
% Here's the (x,y) data to be fitted, followed by the
% weights for each point (set these to 1 if all points
% are equally important).
x = [0.5; 1; 1.5; 2; 2.5; 3; 4; 4.5; 5; 5.5; 6; 7; 7.5];
y = [-0.372; 0.431; 1.69; 2.11; 3.1; 4.23; 4.35;
4.81; 4.61; 4.79; 5.23; 6.35; 7.19];
w = [2; 1.5; 1; 3; 1; 0.5; 1; 2; 2.5; 1; 3; 1; 2];
% Calculate work array lengths, according to the e02be documentation.
m = length(x);
nest = m+4;
lwrk = 4*m + 16*nest + 41;
% Now initialize some parameters required by the nAG routine.
start = 'C';
n = int32(0);
lamda = zeros(nest,1);
wrk = zeros(lwrk, 1);
iwrk = zeros(nest, 1, 'int32');
% Set the smoothness parameter and call the nAG routine to
% compute the cubic spline approximation to the data.
s = 10000.0;
[nOut, lamdaOut, c, fp, wrkOut, iwrkOut, ifail] = ...
e02be(start, x, y, w, s, n, lamda, wrk, iwrk);
% Set up the points at which the spline is to be evaluated.
px = [x(1) : 0.01 : x(m)];
pf = zeros(size(px));
% Now call the nAG routine e02bb to calculate the spline, and plot it.
for i = 1 : length(px)
[pf(i), ifail] = e02bb(lamdaOut, c, px(i), 'ncap7', nOut);
end
plot(px, pf, 'Color', [.8 0 0], 'Linewidth', 2);
Figure 3 にはデータ点、及び s の 3 つの値に対するスプライン曲線が示されています。 s の値が小さくなるとフィット曲線の滑らかさは失われ、 よりデータ点に近いものとなることがこのグラフからわかると思います。
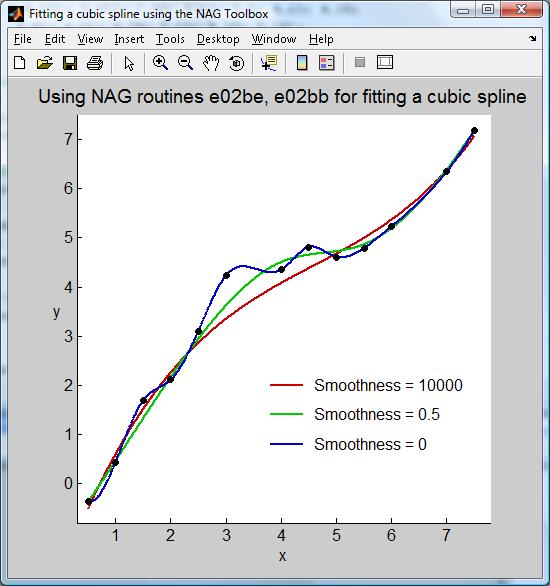
Figure 3: データ点への 3 次スプライン曲線のフィット
The E01 Chapter - Interpolation through a set of points
データ点に対する補間
前の例で s = 0 の場合にはすべてのデータ点を通る 3 次スプライン曲線が求められたので、 与えられたデータ点の範囲内であれば任意のxの値に対し関数値を決定することができたわけです。 この操作は補間と呼ばれ、3 次スプライン曲線は有効な補間曲線であると言えます。 しかし平滑化パラメータの値を決める際のトレードオフに関する議論で見てきたように、 補間の場合にはデータ点間で好ましくない揺動を呈することがあります(Figure 3 における s = 0 の場合の曲線を参照)。
Figure 4 は別のデータに対する 3 次スプライン補間を示したものです。
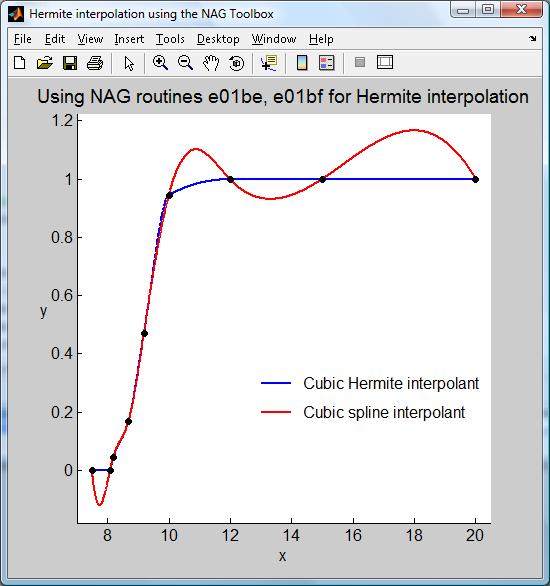
Figure 4: 区分的 3 次エルミート補間曲線を用いたデータ補間
この場合、3 次スプライン補間は x の値が小さい領域で妥当な補間のように見えますが、 端点近傍では大きな揺動を示しています。 これらの揺動は望ましくない場合があります。 例えばデータ値が 1 を越えることはない物理量を表していた場合には、 3 次スプライン曲線の挙動は受け入れがたいものと言えるでしょう。
しかし他の補間曲線を使用することも可能です。 例えば nAG ツールボックスの E01 章には e01be という関数があり、 データ点に対し区分的 3 次エルミート曲線をフィットさせる機能を提供しています。 これは単調性(monotonicity)を維持します。 すなわちデータと同一の区間上において単調増加、あるいは単調減少します。 Figure 4 から見てとれるように、この補間曲線を使用した場合には揺動は発生しないので、 与えられたデータセットに関して言えば物理的により正しい結果を表していると言えるでしょう。
e01be に対するコードは次のとおりです。 これに対しても nAG ツールボックス中には補助的な関数 e01bf が用意されており、e01be の結果に基づき、 任意の点において補間曲線の値を計算することができます。
% Here's the (x,y) data to be fitted. Note that y is
% monotonically increasing.
x = [7.5;
8.09;
8.19;
8.69;
9.19;
10;
12;
15;
20];
y = [0;
0;
0.04375;
0.16918;
0.46943;
0.94374;
0.99864;
0.99992;
0.99999];
% Now call the nAG routine e01be to compute the Hermite interpolant
% through the data.
[d, ifail] = e01be(x, y);
% Set up the points at which the interpolant is to be calculated.
px = [x(1) : 0.01 : x(9)];
% Call the nAG routine e01bf to calculate the interpolant, and plot it.
[pf, ifail] = e01bf(x, f, d, px);
plot (px, pf, '-b', 'LineWidth', 2);
The G Chapter - Creating a Gaussian copula
ガウス型コピュラの作成
最後のセクションでは nAG ツールボックスをより込み入った応用に適用してみます。 統計分野においてコピュラ(copula)は、 多変数分布ファミリーに対する相関構造を規定するものと考えることができます。 ファミリー中の個々の分布は複数の一変数分布を結合させることによって構成されるわけですが、 その際コピュラは接着剤(glue)の役割を果たします。 コピュラは広い範囲のシミュレーション型問題に適用できます。 例えばいわゆるガウス型コピュラは金融モデリングにおいてしばしば使用されます。
例えば今、いくつかのランダム変数の同時分布(joint distribution)をシミュレートしたいものとします。 使用するコピュラの種類(ガウス型、Student の t 分布型、等)によって変数間の相関構造が規定されます。 これに対し一変数の分布の集合(通常周辺分布(marginal distributions)は各変数内における分布を規定します。 より伝統的な多変数分布(例えば多変数正規分布等)の場合と異なり、 コピュラを使用すると個々の変数に異なった周辺分布を持たせることが可能になります。 例えば一つの変数はガウス(正規)型の周辺分布に、 第 2 の変数はベータ分布に、第 3 の変数は一様分布に従うといった設定が可能です。
この例ではベータ型周辺分布を持ったガウス型コピュラを使って 2 変数の分布を作成してみます。 多変数分布の計算に対する入力としては、変数間の相関関係の詳細を規定する共分散行列が必要になります。 コピュラは nAG 関数 g05ra を用いて作成することができます。 ベータ分布の形状は通常 alpha と beta と呼ばれる 2 つのパラメータによって規定され、 正規分布の持つ対称形のベル形状(alpha, beta が共に 1 の場合)から非常に歪んだもの、 あるいは別の極端な場合には一様分布にまで、多岐に及びます。 ここでは第 1 変数に対し alpha = 12.0, beta = 5.0 (歪んだ分布)をセットし、 一方、第 2 変数に対しては alpha = beta = 5.0 (対称型分布)をセットすることにします。 コードは次の通りです。
% Prepare to call the nAG routine g05ra, which generates an array of pseudo-
% random variates from a Gaussian copula. First, initialize some parameters
% required by the routine.
mode = int32(0);
igen = int32(1);
iseed = [int32(1); int32(2); int32(3); int32(4)];
r = zeros(7, 1);
% n is the number of values (actually value pairs) that will be generated.
n = int32(10000);
% Next, set the correlation coefficient for the two variables, and use it
% to construct the (upper triangle of the) covariance matrix of the
% distribution.
corr = 0.8;
c = [1.0, corrl;
0.0, 1.0;];
% Call g05ra to generate the array of variates.
[x, iseedOut, rOut, ifail] = g05ra(mode, c, n, igen, iseed, r);
% Now set the parameters for the two marginal distributions...
alpha1 = 12.0;
beta1 = 5.0;
alpha2 = 5.0;
beta2 = 5.0;
% ...and call g01fe to compute the deviates from the Beta distribution.
tol = 1.0;
for ii = 1 : n
[x(ii,1)] = g01fe(x(ii,1), alpha1, beta1, tol);
[x(ii,2)] = g01fe(x(ii,2), alpha2, beta2, tol);
end
結果の分布は 2 次元の度数分布配列に変換され、MATLAB® 上では曲面として表示されます(等高線図等、 他の表現も可能です)。
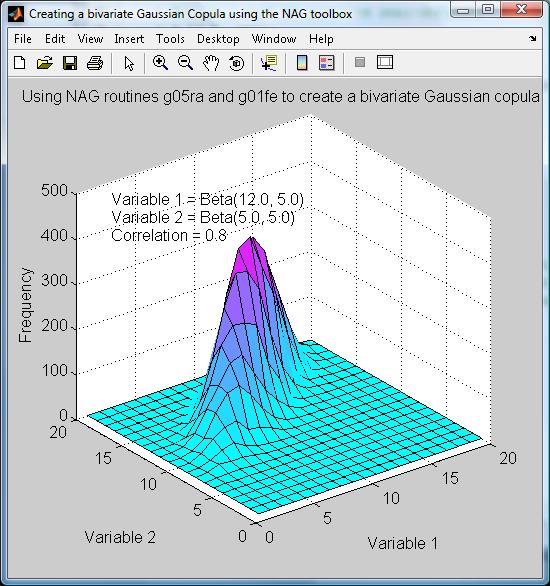
Figure 5: ガウス型コピュラの作成
周辺分布を別のものにしたとき、あるいは相関係数を変化させたとき、 コピュラの形状がどう変化するかを調べるのはためになります。 例えば相関係数を増やせばピークがより狭いものとなります。 また MATLAB® ではパラメータ値をループさせることによってアニメーションを比較的容易に作成できます。 これによって 2 次元の領域上におけるピークの動きを追跡するといったことが可能になります。
