nAG ツールボックスにより nAG ライブラリの全機能が MATLAB® から使えるようになります。 MATLAB® を介して nAG ライブラリをコールする利点は、多くの引数の指定が任意あるいは不要になることで、 コードを読みやすく保守しやすいものにすることができます。
nAG ライブラリのすべてのドキュメント(印刷物だと 17 冊、本棚で約 1m の幅になります)は、 MATLAB® ヘルプ形式に変換されているため、MATLAB® からのアクセスは容易に行えます。 それぞれの nAG ライブラリ関数に対する記述の中には、それの用法を示す MATLAB® コードの例が含まれています。
この新たなツールボックスの利用がいかに簡単であるかを示すために、 いくつかの代表的な nAG 関数を例にとってその用法、 及び結果を MATLAB® のプロット機能で表示させる方法について説明します。
- Part 1 に引き続き Part 2, Part 3 はこちらからご参照いただけます。
nAG Toolbox for MATLAB® 製品の使用例 - Part 3
The S chapter - Bessel functions
ベッセル関数
まず最も簡単な nAG ライブラリコールのいくつかから見て行くことにしましょう。 S 章には他の多くの特殊関数と共にベッセル関数 Y0(x), Y1(x), J0(x), J1(x) に関する記述が含まれています。 nAG における通常のネーミングルールに従うと、これらは各々 s17ac, s17ad, s17ae, s17af 関数に対応します。
次に示すのはその用例で、いくつかのプロットコマンドも含まれています。
% Evaluate the Bessel functions at a set of points in x x = [0.125, 0.25 : 0.25 : 40]; for i = 1 : length(x) [y0(i), ifail] = s17ac(x(i)); [y1(i), ifail] = s17ad(x(i)); [j0(i), ifail] = s17ae(x(i)); [j1(i), ifail] = s17af(x(i)); end % Plot the results. Note that we omit the first two values of Y1(x) % because they are large and would spoil the scaling of the graph. hold on; plot(x, y0, 'Color', 'red'); plot(x(3:length(x)), y1(3:length(x)), 'Color', 'green'); plot(x, j0, 'Color', 'blue'); plot(x, j1, 'Color', [1.0 1.0 0.0]);
結果のグラフは次のようになります。
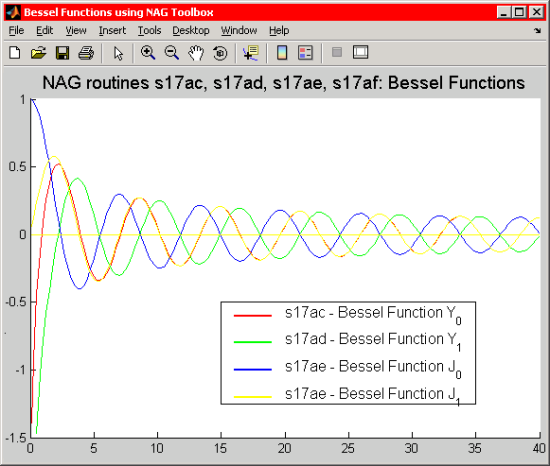
Figure 1: ベッセル関数
The E02 Chapter - Fitting a surface with bicubic splines
双 3 次スプラインによる曲面のフィット
多くの科学分野において、一群のデータ点を近似する関数形を見つけることがしばしば必要になります。 通常、データには測定誤差等のランダムな擾乱が含まれているため、 それらを平滑化し除去した方が良い場合が良くあります。
e02dc は x-y 平面内の矩形グリッド上で与えられた一群のデータ値に対する双 3 次(bicubic)スプライン近似を計算します。 フィットの適合度とスムーズさをバランスさせるためのパラメータが指定されています。
e02dc 中では s という名称のついた平滑化パラメータは、 その値が小さいほどデータへのフィットが完全に近いものとなります。 しかしここで言う“小さい”という表現の意味はそれぞれのデータセットごとに異なります。 s = 0 とした場合には理論上、補間スプライン曲線が得られることになりますが、 現実問題としてはオリジナルデータの周囲で大きく振動する曲面となってしまうことがあります。
% Create an arbitrary data set consisting of a plane with three peaks
x = [0; 0.5; 1; 1.5; 2; 2.5; 3; 3.5; 4; 4.5; 5];
y = [0; 0.5; 1; 1.5; 2; 2.5; 3; 3.5; 4];
f = [1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1;
1; 1; 1.1; 1.2; 1.1; 1; 1; 1; 1; 1; 1;
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1;
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1;
1; 1; 1; 1; 1; 1.075; 1.15; 1.075; 1; 1; 1;
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1;
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1.1;
1.2; 1.1; 1; 1; 1; 1; 1; 1; 1; 1;
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1];
% The smoothing parameter. A smaller value of s gives a closer fit.
s = 0.0175593;
% Set the coordinates of the rectangular grid.
px = 0 : 0.1 : 5.0;
py = 0 : 0.1 : 4.0;
% Initialize some quantities required by e02dc
start = 'C';
nx = int32(0);
lamda = zeros(15,1);
mu = zeros(13,1);
ny = int32(0);
wrk = zeros(592, 1);
iwrk = zeros(51, 1, 'int32');
% Compute the bicubic spline approximant with e02dc
[nxOut, lamdaOut, nyOut, muOut, c, fp, wrkOut, iwrkOut, ifail] = ...
e02dc(start, x, y, f, s, nx, lamda, ny, mu, wrk, iwrk);
% Evaluate the spline on a rectangular grid using e02df
[ff, ifail] = e02df(px, py, lamdaOut(1:nxOut), muOut(1:nyOut), c);
Figure 2 はオリジナルデータを、Figure 3 はそれに対するスムーズな双 3 次スプライン近似を示すものです。
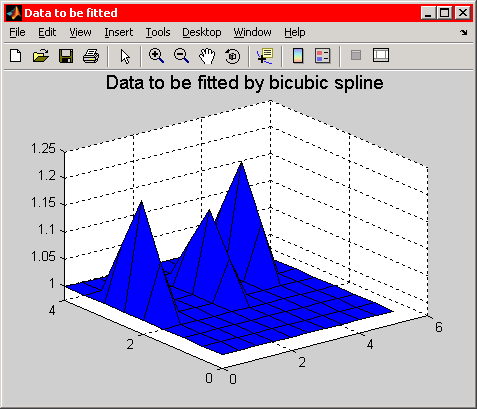
Figure 2: 双 3 次スプラインによるフィット対象のデータ
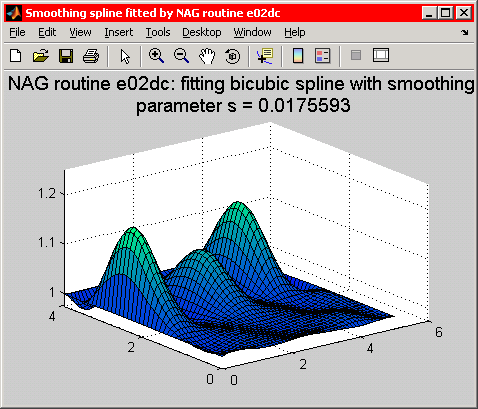
Figure 3: 矩形グリッド上で評価された双 3 次スプライン
The E04 Chapter - Minimization of a function
関数の最小化
nAG 関数 e04wd は逐次二次計画法(SQP: sequential quadratic programming) を用いて任意の滑らかな関数の最小値を探索するもので、線形、 あるいは非線形の制約条件が付帯していても構いません。 この手法の詳細については e04wd のドキュメントをご参照ください。
ここでは良く知られたローゼンブロック(Rosenbrock)関数、すなわち
f(x,y) = 100*(y-x*x)^2 + (1-x)^2
で与えられる 2 変数関数の最小値を求めるのに e04wd を使用してみます。
ローゼンブロック関数の最小値を求める問題には制約条件は課されません。 最小点を与える x, y としては任意の値が許容されます。
ローゼンブロック関数の特徴である“バナナ型の谷”を表す等高線形状(下図参照)により、 この関数は e04wd のような最小化機能に対する検証用の問題としてしばしば利用されます。 ベーシックな最急降下(steepest descent)法のような単純なアルゴリズムでは浅く カーブした谷底を這う際に最小点がうまく見出せないことが起こりますが、 nAG 関数ではそのような問題は発生しません。
e04wd の一つの特長は、 最小化の対象となる関数の 1 次導関数が解析的な形で与えられていなくても良いという点にあります。 これらの 1 次導関数が与えられていない場合、あるいは求めるのが難しい場合、 e04wd は差分近似によってそれらの値を推定します。 しかし 1 次導関数をユーザが指定した場合には、収束はより早く、 かつ頑健なものとなります。
評価対象の関数は MATLAB® の .m ファイルとして e04wd に与えられます。 ここでは objfun.m というファイル名を用いることにします。 e04wd は必要に応じて目的関数の 1 次導関数の値も評価します。 導関数がわからないときはどうしたら良いでしょうか。 計算する必要はありません。 e04wd は導関数が与えられたかどうかを判定し、 必要な場合には自分で導関数の値を推定します。
objfun.m ファイルの内容は次のようになります。
function [mode, objf, grad, user] = ...
objfun(mode, n, x, grad, nstate, user)
objf = 100*(x(2)-x(1)^2)^2 + (1 - x(1))^2;
if (mode == 1 || mode == 2)
% Derivatives: grad(i) is the derivative with
% respect to x(i), for i = 1, 2.
grad(1) = 2*(1-200*x(2))*x(1) + 400*x(1)*x(1)*x(1) - 2;
grad(2) = 200*(x(2) - x(1)*x(1));
end
e04wd をコールするためのコードを次に示します。
% There are no linear or nonlinear constraints
a = [];
istate = zeros(2, 1, 'int32');
ccon = [];
cjac = [];
clamda = zeros(2,1);
hess = zeros(2,2);
% Arbitrary bounds on the variables
bl = [-10; -10];
bu = [10; 10];
% Initial guess at solution
x = [-2.75; 2];
% Initialize the minimization routine e04wd using e04wc
[iw, rw] = e04wc();
% Array user can contain anything we want. It lets us
% communicate with objfun.
user = [0,0,0,0,0];
% Solve the problem using nAG routine e04wd.
[majits, istateOut, cconOut, cjacOut, clamdaOut, objf, grad, ...
hessOut, xOut, iwOut, rwOut, user] = ...
e04wd(a, bl, bu, 'confun', 'objfun', istate, ...
ccon, cjac, clamda, hess, x, iw, rw, 'user', user);
objfun.m 中の関数と同様に、e04wd は非線形の制約関数を評価する上で関数 confun.m も必要とします。 しかし今の場合、制約関数は存在しないのでダミーを使用しています。
また明確さを期するために、等高線や結果をプロットするための MATLAB® コマンドはすべて省略してあります。
次の図は導関数が解析的な形で指定されたときのローゼンブロック関数の最小値探索パスを示しています。 目的関数の評価が行われるたびに、その点がプロットされています。始点は青の円で、 またターゲットである最小点は (1,1) の位置に緑の円で示されています。 パスが後ろ向きにトレースされ、最小点に向かうパスに自動的に戻されている点に注意してください。
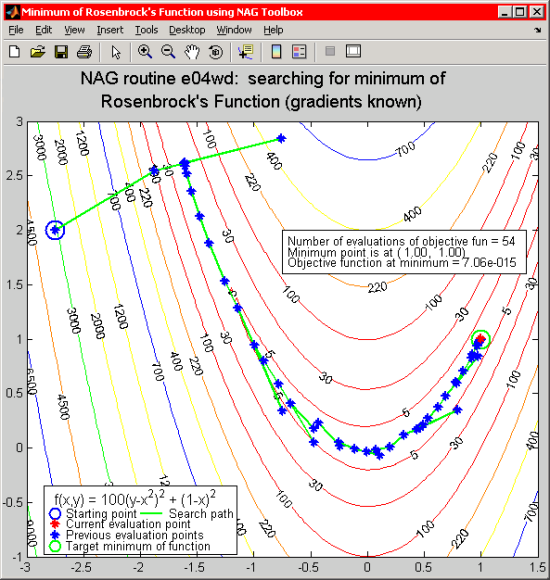
Figure 4: ローゼンブロック関数の最小値に至るパス(導関数が与えられた場合)
導関数が与えられなくても e04wd が機能することを示すため、objfun.m 中の関数を次のコードで置き換えます。
function [mode, objf, grad, user] = ...
objfun(mode, n, x, grad, nstate, user)
objf = 100*(x(2)-x(1)^2)^2 + (1 - x(1))^2;
% We don't compute derivative information
end
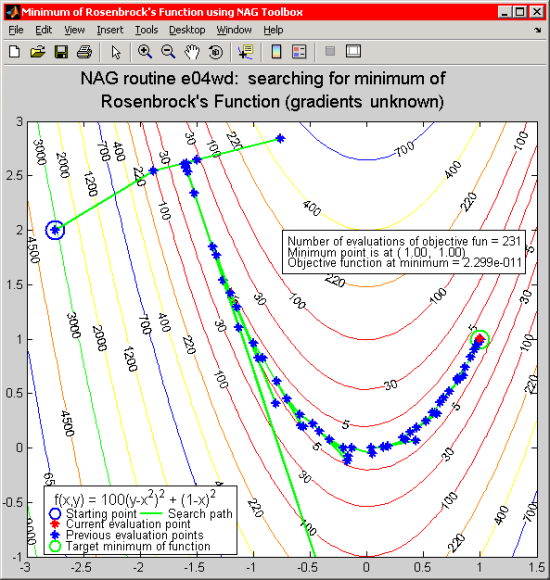
Figure 5: ローゼンブロック関数の最小値に至るパス(導関数が与えられなかった場合)
この場合、導関数に関する情報が欠落しているために探索はむずかしくなります。 e04wd は目的関数に関し余分の評価を行うことによって導関数値の推定を行います。 導関数が与えられたときには 54 回の評価で済んでいたものが、 今のケースでは計 231 回の評価が必要となっています。 また得られた最小値も厳密解である 0.0 に近いものの、 期待されたほど良い値とは言えません。
教訓: なるべく導関数を指定してください。 しかしできない場合には nAG 関数に一任させることも可能です。
