Keyword: 実対称正定値, 連立一次方程式, 誤差限界
概要
本サンプルは実対称正定値連立一次方程式の解及び誤差限界を求めるC言語によるサンプルプログラムです。 本サンプルは実対称正定値行列Aと行列Bが以下に示される場合の連立一次方程式 AX=B の解を求め、さらに条件数や誤差限界の推定値を算出して出力します。
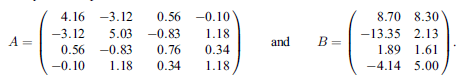
※本サンプルはnAG Cライブラリに含まれる関数 nag_real_sym_posdef_lin_solve() のExampleコードです。本サンプル及び関数の詳細情報は nag_real_sym_posdef_lin_solve のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はnag_real_sym_posdef_lin_solve のマニュアルページを参照)| このデータをダウンロード |
nag_real_sym_posdef_lin_solve (f04bdc) Example Program Data
4 2 :Values of n and nrhs
Nag_Upper :Value of uplo
4.16 -3.12 0.56 -0.10
5.03 -0.83 1.18
0.76 0.34
1.18 :End of matrix A
8.70 8.30
-13.35 2.13
1.89 1.61
-4.14 5.00 :End of matrix B
- 1行目はタイトル行で読み飛ばされます。
- 3行目に行列Aの次数(n)、行列Bの列数(nrhs)を指定しています。
- 4行目に行列Aの上三角部分を格納するか下三角部分を格納するか(uplo)を指定しています。"Nag_Upper"は上三角部分を格納することを意味します。
- 5〜8行目に行列Aの要素を指定しています。
- 10〜13行目に行列Bの要素を指定しています。
出力結果
(本関数の詳細はnag_real_sym_posdef_lin_solve のマニュアルページを参照)| この出力例をダウンロード |
nag_real_sym_posdef_lin_solve (f04bdc) Example Program Results
Solution
1 2
1 1.0000 4.0000
2 -1.0000 3.0000
3 2.0000 2.0000
4 -3.0000 1.0000
Estimate of condition number
9.7e+01
Estimate of error bound for computed solutions
1.1e-14
- 5〜9行目にxの解が出力されています。
- 12行目に行列Aの条件数の推定値が出力されています。
- 16行目に解の誤差限界の推定値が出力されています。
ソースコード
(本関数の詳細はnag_real_sym_posdef_lin_solve のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_real_sym_posdef_lin_solve (f04bdc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*/
#include <stdio.h>
#include <nag.h>
#include <nag_stdlib.h>
#include <nagf04.h>
#include <nagx04.h>
int main(void)
{
/* Scalars */
double errbnd, rcond;
Integer exit_status, i, j, n, nrhs, pda, pdb;
/* Arrays */
char nag_enum_arg[40];
double *a = 0, *b = 0;
/* Nag Types */
Nag_OrderType order;
Nag_UploType uplo;
NagError fail;
#ifdef nAG_COLUMN_MAJOR
#define A(I, J) a[(J-1)*pda + I - 1]
#define B(I, J) b[(J-1)*pdb + I - 1]
order = Nag_ColMajor;
#else
#define A(I, J) a[(I-1)*pda + J - 1]
#define B(I, J) b[(I-1)*pdb + J - 1]
order = Nag_RowMajor;
#endif
exit_status = 0;
INIT_FAIL(fail);
printf("nag_real_sym_posdef_lin_solve (f04bdc) Example Program Results\n\n");
/* Skip heading in data file */
scanf("%*[^\n] ");
scanf("%ld%ld%*[^\n] ", &n, &nrhs);
if (n >= 0 && nrhs >= 0) {
/* Allocate memory */
if (!(a = nAG_ALLOC(n * n, double)) || !(b = nAG_ALLOC(n * nrhs, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
#ifdef nAG_COLUMN_MAJOR
pda = n;
pdb = n;
#else
pda = n;
pdb = nrhs;
#endif
}
else {
printf("%s\n", "n and/or nrhs too small");
exit_status = 1;
return exit_status;
}
scanf("%39s%*[^\n] ", nag_enum_arg);
/* nag_enum_name_to_value (x04nac).
* Converts nAG enum member name to value
*/
uplo = (Nag_UploType) nag_enum_name_to_value(nag_enum_arg);
if (uplo == Nag_Upper) {
/* Read the upper triangular part of A from data file */
for (i = 1; i <= n; ++i) {
for (j = i; j <= n; ++j) {
scanf("%lf", &A(i, j));
}
}
scanf("%*[^\n] ");
}
else {
/* Read the lower triangular part of A from data file */
for (i = 1; i <= n; ++i) {
for (j = 1; j <= i; ++j) {
scanf("%lf", &A(i, j));
}
}
scanf("%*[^\n] ");
}
/* Read B from data file */
for (i = 1; i <= n; ++i) {
for (j = 1; j <= nrhs; ++j) {
scanf("%lf", &B(i, j));
}
}
scanf("%*[^\n] ");
/* Solve the equations AX = B for X */
/* nag_real_sym_posdef_lin_solve (f04bdc).
* Computes the solution and error-bound to a real symmetric
* positive-definite system of linear equations
*/
nag_real_sym_posdef_lin_solve(order, uplo, n, nrhs, a, pda, b, pdb,
&rcond, &errbnd, &fail);
if (fail.code == NE_NOERROR) {
/* Print solution, estimate of condition number and approximate */
/* error bound */
/* nag_gen_real_mat_print (x04cac).
* Print real general matrix (easy-to-use)
*/
fflush(stdout);
nag_gen_real_mat_print(order, Nag_GeneralMatrix, Nag_NonUnitDiag, n,
nrhs, b, pdb, "Solution", 0, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_gen_real_mat_print (x04cac).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
printf("\n");
printf("%s\n%6s%10.1e\n", "Estimate of condition number", "",
1.0 / rcond);
printf("\n\n");
printf("%s\n%6s%10.1e\n\n",
"Estimate of error bound for computed solutions", "", errbnd);
}
else if (fail.code == NE_RCOND) {
/* Matrix A is numerically singular. Print estimate of */
/* reciprocal of condition number and solution */
printf("\n%s\n%6s%10.1e\n\n\n",
"Estimate of reciprocal of condition number", "", rcond);
/* nag_gen_real_mat_print (x04cac), see above. */
fflush(stdout);
nag_gen_real_mat_print(order, Nag_GeneralMatrix, Nag_NonUnitDiag, n,
nrhs, b, pdb, "Solution", 0, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_gen_real_mat_print (x04cac).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
}
else if (fail.code == NE_POS_DEF) {
/* The matrix A is not positive definite to working precision */
printf("%s%3ld%s\n\n", "The leading minor of order ",
fail.errnum, " is not positive definite");
}
else {
printf("Error from nag_real_sym_posdef_lin_solve (f04bdc).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
END:
nAG_FREE(a);
nAG_FREE(b);
return exit_status;
}
