プログラムの高速化・並列化サービスの事例

概要

Fluidityは非定常の有限要素/コントロールボリュームを用いた前進差分CFDで、地球力学、海洋モデリングおよび地球物理学的流体力学などの様々な領域で用いられています。このアプリケーションは、実験室レベルから地球のマントルシミュレーションまでの幅広い領域をカバーしています。Fluidityの特徴は、動的アダプティブメッシュ(dynamic adaptive remeshing)により、メッシュを計算中に適合させることが可能な点です。マルチプロセッサー上で実行した場合、アダプティブメッシュは、要素をプロセッサー間で移動させて負荷を均等化させる必要があります。Zoltanはこのような動的負荷バランスのためのライブラリーです。本レポートは、その適用可能な領域を拡張する、ZoltanのFluidityへの組込みについて記述します。現状のカスタマイズされた負荷バランスライブラリーによる性能向上はそれほど大きくなく、プロセス当たりの要素数が小さい場合にのみ認められています。

１．目的と目標

本プロジェクトの目的は、Fluidity(Piggott et al., 2009; Gorman, 2006)の並列計算における非等方性メッシュのアダプティビティと負荷バランスアルゴリズムを、非構造でアダプティブかつ動的なアプリケーションに対するデータ管理セットであるZoltanの組込みにより改善することです。狙いは、Fluidityのスケール性能の改善、およびアダプティブ・リメッシュアルゴリズム(Pain et al., 2001)を、単一要素ペアに拘らずいかなる要素ペアに対しても並列で動作させることです。

Zoltanには、並列領域分割アルゴリズム、データマイグレーションツール、並列グラフ色分けツール、分散データディレクトリー、非構造化データサービス、および動的メモリー管理ツールを統合したものが含まれます。Zoltanの組込みにより、並列性能の改善だけでなく、ソフトウェア持続性の改善と新たな機能追加も可能です。これは、FluidityにPRACEプロジェクトで提案されたようなペタフロップス・システムでの実行を準備する新たな能力を持ち込み、その能力との結合は新たなサイエンスの実行を可能にするでしょう。

Fluidityのアダプティビティに追加される新たな特性に加えて、Zoltanの組込みは他のモデルを扱うことが可能になります。それは将来の研究のカギとなる大気および氷床モデルで、標準的でない離散化を要求されるモデルです。Fluidityで最近開発されたのは、ラグランジュ粒子描像の追加です。これは流れの中の自由粒子で、ディテクターとして、あるいはエージェントベース・モデリングにおいて用いられます。これには並列化が要求されますが、メッシュと粒子間の対立する負荷バランスを考えれば、それは自明な事ではありません。このような目的のための負荷バランスおよび並列データマイグレーション・アルゴリズムは既にZoltanに備わっており、本プロジェクトにおいて役に立つものです。

本プロジェクトは、以下の6つの作業を設定されました：

1.	コードとそのビルドおよびベンチマークについて計算、通信、データマイグレーションおよびアダプティビティに関する詳細なタイミングデータレポートを作成する。
2.	並列アダプティビティに対するZoltan解法の追加は、Fluidityのコンパイルオプションとして指定するようにする。ParMETISへのZoltanインターフェイスを用いて、これまでの解法の機能を再現し、Zoltan解法を使用した場合はFluidityの全てのテスト(unit,short,medium,long)をパスすることを示す。従来の解法とZoltanの機能を比較する新たなテストと、Zoltanの通信機能のunitテストを行う。実装の詳細をレポートする。
3.	Zoltan解法は、Fluidityの開発ブランチ全てと将来のリリースにおいてデフォルトとして用いる。Zoltanの全ての開発ブランチをマージして全てのテストをパスすること。FluidityおよびFluidityオプションシステム「Diamond」(Ham et al., 2009)マニュアルへZoltanオプションを記載する。
4.	様々なZoltanオプションを用いたFluidityの性能改善を、Fluidityオプションシステムを用いて調査する。目標は、全てのHPCベンチマークにおいて、以前の解法にたいしてZoltan解法を用いた場合の方が、通信時間が15%以上削減されることである。64から2048プロセスに関し、以前の解法に比べZoltanを用いた場合15%の性能向上を示すこと。
5.	最終レポートには全てのHPCベンチマークのプロファイル結果を含める。
6.	FuidityのHPCワークショップへ参加し、最新の状況を報告する。

本レポートは、Fluidityの背景説明から始めて、アダプティビティおよび並列アダプティビティのFluidityにおける実装アルゴリズムを示します。次にZoltanライブラリーを議論します。その後、実装およびHECToR上でのHPCベンチマークのプロファイル結果を示します。最後に、本プロジェクトの成果の詳細とHECToRユーザーにとっての利点を、結論として記します。

２．背景

２．１　Fluidity

Fluidityは、一般目的のマルチフェーズ計算流体力学オープンソースコードであり、1,2,3次元の任意の非構造有限要素メッシュ上での、Navier-Stokes方程式と場の方程式を解きます(Piggott et al., 2009; Pain et al., 2005)。Fluidityは、地球物理学的流体力学(Mitchell et al., 2010)や、計算流体力学(Hiester et al., 2011)、海洋モデリング(Pain et al., 2005)、マントル対流(Davies et al., 2011)など、様々な領域で利用されています。Fluidityは、有限要素/コントロールボリューム法を用い、時間依存の問題にメッシュの任意の動きを可能にし、その時点の状態に応じて局所的にメッシュ解像度を増減させることが出来ます(図1)。また幅広いメッシュ選択とその混成も可能です。FluidityはMPIで並列化されており、HECToR上の数千プロセッサーを用いてスケールする能力を持ちます。革新的な新規の特徴としてその他にはユーザーフレンドリーなGUI「Diamond」(Ham et al., 2009)、および診断場の計算や、既定場の設定、ユーザー定義境界条件の設定に用いるpythonインターフェイスがあります。

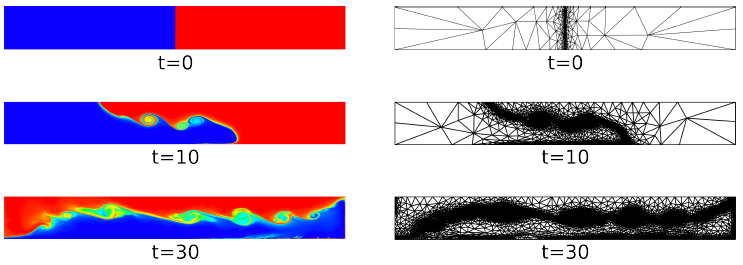
図1　：　Fluidityのアダプティブ・メッシュ・シミュレーションによる水門開放問題(lock-exchange problem)例。アダプティブ・メッシュは、温度場(赤色と青色)と速度(これは示していない)に対して適用された。このメッシュは形状曲率が存在する場合にリファインされ、このインターフェイスを保存しつつ総計算負荷を削減する(Hiester et al.,2011)

２．２　アダプティビティ

以降アダプティビティと呼ぶ動的アダプティブ再メッシュ化は、現状のモデル状態とユーザーが定義した関数により、ある誤差に従ってメッシュを適合(adapt)させるプロセスです。これは、"事後"メトリックを用いて、シミュレーションの進行に合わせてメッシュを変更させることを可能にするものです。"事後"メトリックが計算出来れば、所望の誤差へ近づかせるために離散化を修正する様々な手法を用いることが出来ます。これらには、メッシュの結合を変更するh法(h-adaptivity、Berger and Colella, 1989)、近似多項式次数を増やすp法(p-adaptivity、Babuška and Suri, 1994)、同じ結合を保ちつつメッシュ頂点を移動させるr法(r-adaptivity、Budd et al., 2009)があります。

Fluidityは、h法とr法を組合せた強力な方法(hr-adaptivity)を用い、生成されたメッシュは前のメッシュから制約を受けないことから、この手法は解の特性への適合において最も柔軟に対応可能なものとなっています。しかしながらこの柔軟さはコストへ反映されます：これには、アダプティブ・メッシュの指示(どのメッシュを構築するかを選択する)、アダプテーションの実行(選択されたメッシュの構築)、および解かれた場のデータ変換(前のメッシュから更新されたアダプティブ・メッシュへ)などがあり、階層的なリファインの場合よりもさらに複雑です。

アダプティビティが実行されるメトリック$M$は、以下のように計算されます。各場$f_i$は以下のようにメトリックに含まれます：

\begin{eqnarray} M_i=\frac{1}{\epsilon_{f_i}}|H(f_i)| \tag{1} \end{eqnarray}

ここで、$\epsilon_{f_i}$はユーザー定義の重みで、$|H(f_i)|$はヘッシアン行列の固有値の絶対値を用いた行列です。テンソルの使用により非等方性の方向情報を含むため、これはアダプティビティに影響を与えます。

アダプティビティのアルゴリズムは以下のステージに従って実行されます(図2も参照してください)：

1.	ユーザーが誤差メトリックに含めるように指定した場のヘッシアンを構築する。これは、エッジ長の最小、最大値等のユーザー定義パラメーターに依存します。
2.	このヘッシアンを上述のようにメトリックテンソルへ変換する。
3.	各場のメトリックテンソルを一つのメトリックへ集約する。
4.	メッシュサイズ内で不連続にならないように、メッシュの段階的な変化に合わせてメトリックを滑らかにする。
5.	ノードの最大数のような、メトリック上のユーザー定義の拘束条件を適用する。
6.	このメトリックを、それに基づく新しいメッシュ生成を行うアダプティビティ・ライブラリーへ渡す。
7.	内挿により元のメッシュから新しいメッシュへ場を変換する(Farrell,2011)

さらに詳細なアルゴリズムと方法については、Fluidityのマニュアルと文献(Farrell et al. 2009)を参照してください。

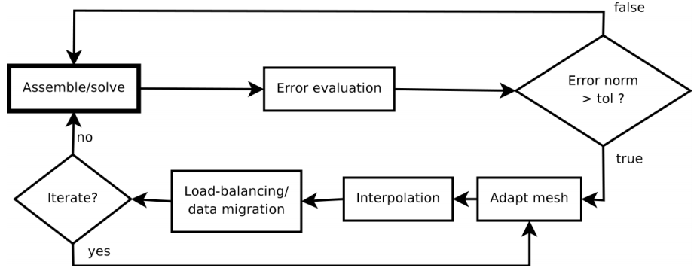
図2 ：　Fluidityが使用する並列アダプティビティのアルゴリズム

２．３　並列アダプティビティ

前節で記述されたFluidityで用いられるアダプティビティ手法は、シリアルプロセスです。MPIによるこの手法の並列化は、かなりの複雑さと多くのプロセス間通信を必要とします。このやり方のレビューが文献Farrell et al. 2009で与えられています。ここでは以下のアプローチを取ります(図3)：

1. 各プロセスはそのローカルメッシュを更新します。ただしハロ交換は除きます。この更新には前セクションのアルゴリズムを用います。
2. メッシュは再分割されます。ただし要素品質以下の要素については大きなedge weightを適用します。
3. 繰り返し回数分(デフォルトは3)上記2ステップを繰り返します。
4. 最後に、メッシュの負荷バランスのためにedge weightを適用せず、メッシュを再分割します。

この手法は、前に記述したシリアル版のアダプティビティ手法で、ハロに存在しない全ての要素を更新するやり方です。ハロに在る要素も別のプロセスとして存在しますが、これらが同様に更新される場合はリモートプロセスとの通信が必要になります。ハロの要素を固定すれば、通信は回避できますが、局所アダプティビティステップ後に固定された要素は更新されておらず、品質を落とします。品質が劣化した要素へ大きなedge weightを適用して再分割すると、その要素は分割されないため、領域の中央に存在することになり、次のアダプティビティステップで更新されることになります。現状の負荷の再バランスを行う専用コードは、Sam Gorman (2006)により構築されました。これは区間線形要素のみに対して行われ、領域内でディテクターや周期性を用いていません。これは専用コードであり、新たな要素ペアについてデータマイグレーションを実行するためには専用のコードが必要です。これには、要素と場のデータを同時にマイグレーションするような、Zoltanに無い最適化が必要となります。

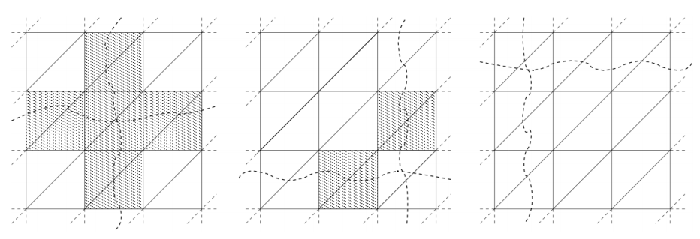
図3 ：　2Dメッシュの例。ここで分割は波破線で示されています。左図では最適化前の拘束された要素(灰色)が多角形で存在します。中央の図では再分割後に孤立した要素のみが残っています。右図では、全ての要素が更新されています。

２．４　Zoltan

Zoltanは領域分割、負荷バランスおよびデータ管理ルーチンの並列ライブラリーです(Devine et al., 2002; Boman et al., 2007)。これはサンディア国立研究所によりオープンソースライブラリーとして開発されました。Zoltanは、同じくサンディア国立研究所のTrilinosパッケージの一部としても使用されています。Zoltanは様々な異なる領域分割ライブラリー；ParMETISやPT-Scotch、また、自身が持つグラフ分割やハイパーグラフ分割ライブラリーを利用できます(Catalyurek et al., 2009)。これらの特徴から、Fluidityの現状コードを置き換えることが可能です。

３．実装

実装では、Zoltanの負荷バランスとデータマイグレーション関数であるZoltan_LB_BalanceおよびZoltan_Migrateを用いました。ここでは補助的な関数として、send/receiveリストを反転させる関数Zoltan_Invert_Listsも使用しました。このセクションでは、実装の概要と、その構造の詳細について記述します。
実装の基本的な概略は以下の通りです：

1. モジュール変数の準備
2. Zoltanパラメーターの設定
3. Zoltanコールバック関数の登録
4. メッシュ生成ノードの負荷バランスをとる
5. 各ノードをデータマイグレーションする
6. ハロリストを構築する
7. ハロノードをデータマイグレーションする
8. 新しいメッシュとデータ構造を構築する
9. 新しいメッシュに場をアロケーションする
10. 新しいメッシュ状の各要素の場のデータを転送する
11. モジュール変数をクリーンアップする

これら全てのステップは、FortranモジュールとしてZoltan_integration、Zoltan_callbacksおよびZoltan_global_variablesへ実装されました。Zoltan_integrationのサブルーチンzoltan_driveは上述のプロセスが実装され、Fluidityから呼ばれるのはこのルーチンです。Zoltan_callbacksは、Zoltanへ提供される全てのコールバック関数を含んでいます。Zoltan_global_variablesは、様々なFluidityの変数と、Zoltan_integrationとZoltan_callbacksで共有するデータ構造を設定・準備します。不運にもグローバル変数が必要となりますが、これはZoltanの固定インターフェイスで必要とされるコールバックのためで、コールバック関数内で必要とされるFluidityのデータ構造にアクセスする唯一の方法です。

補助関数Zoltan_Invert_Listsは、各プロセスに自身が必要とするノードや要素のリストを作らせるのに便利です。各プロセスが作るリストは、関数Zoltan_Migrateにより要求される受信リストで、Zoltan_Invert_Listsにより同様に要求される送信リストを得ることが可能です。これ以上の詳細についてはFluidityのデータ構造に深く立ち入るため、より詳細についてはソースコードを参照してください(https://launchpad.net/fluidity)。

３．１　コールバック

Zoltanは一般用途向けの再領域分割およびデータ分散並列ライブラリーで、データ非依存です。よってコールバック関数を使って、Zoltanが呼び出されている間にFluidityのデータ構造から所望の情報取得のための照会機能が提供さされるべきです。Fluidityには4つのコールバック関数があります；一つは負荷バランスのために、残りの3つは、ローカルノード、ハロノードおよび場のデータマイグレーション用です。本レポートではコールバック関数の簡単な概要のみを記載します。

３．２　負荷バランス

Zoltan_LB_BalanceあるいはZoltan_LB_Partの呼出しに際しては、Zoltanはグラフを作るノードや、そのノードがどのように結合しているか、エッジに関してのみ考慮します。これらコールバック関数は以下の機能を提供しなくてはなりません：

1.	ローカルノード数
2.	ローカルノードリスト
3.	各ローカルノードに関するエッジ数
4.	各ローカルノードに関するエッジリスト(エッジが接する隣のノード)

ノードとエッジのリストを提供する際には重みも提供されます。この実装の中で、不均一ノードのウェイトが適用されるのは押し出しメッシュを用いる場合のみです(押し出しメッシュは、2D表面から重力方向に押し出されて3Dメッシュを生成したものです)。重みづけ(Weighting）はエッジに対してより頻繁に用いられるため、セクション2.3で述べたようにFluidityでの並列アダプティビティ手法の鍵となります。
Edge weightingは、コールバック関数zoltan_cb_get_edge_listで行われます。このコールバックは各ローカルノードの各エッジと、エッジが接する隣のノード、および現在どのプロセスがその隣接ノードを所有しているかを提供しなくてはなりません。また各エッジのedge weightも提供することとしました。以下の疑似コードが実装の詳細です。

Listing1:edge weighting pseudo-code

For node = 1 to # localnodes
　Store global id for each neighbouring node
　Store owning process for each neighbouring node
　For element = 1 to # elements associated with local node
　　Determine element quality
　　if(quality < local minimum quality)
　　　local minimum quality = quality
　for nbor_node = 1 to # neighbouring nodes
　　for element = 1 to # elements associated with neighbor node
　　　determine element quality
　　　　if(quality < neighbor minimum quality)
　　　　　neighbor minimum quality = quality
　　　min_quality = min(nbor_min_quality,local_min_quality)
　　　if(min_quality < element_quality_cutoff)
　　　　edge_weight = ceil((1.0 - min_quality) * 20)
　　　else
　　　　edge_weight = 1.0

my_max_weight = max(my_edge_weights)
my_min_weight = min(my_edge_weights)
MPI_AllReduce(my_max_weight,max_weight,1,MPI_FLOAT,MPI_MAX)
MPI_AllReduce(my_min_weight,min_weight,1,MPI_FLOAT,MPI_MIN)

Ninety_weight = 0.9 * max_weight
!　avoid adjusting the weights if all elements are similar quality
if(min_weight < ninety_weight)
　for edge_weight = 1 to # total_edges
　　if(edge_weight > ninety_weight)
　　　edge_weight = num_total_edges + 1

この実装は、全ローカルノード上でループし、各ノードに対してグローバルIDとその隣接ノードを持つプロセスを記録します。次に、ローカルノードとその隣接ノード間のエッジに適用するedge weightを計算します。この狙いは低品質の要素へ大きなedge weightを適用することです。このために最初に、ローカルノードの最も低品質な要素を決定します。次に、隣接ノードの最も低品質な要素を決定します。ローカルノードと隣接ノードの両方に対する最低品質要素を、ローカルノードと隣接ノード間のエッジへ適用するウェイトの計算に用います。

全てのedge weightが計算された時点で、最低品質の要素のノードはこの時、シミュレーション内のエッジ総数よりも大きな値に設定されたedge weightを持つことになります。つまりこれは分割されないことを意味します。任意のプロセスの最大edge weightの10％以内であると算出されたedge weightを持つエッジは、そのような量を与えられています。

edge weightingはこのように実装され、Fluidityで用いられている以前のメッシュ分割の動きを再現します。しかしながらZoltanを用いた場合は、edge weightが正しく適用されている場合でも、メッシュ再分割が低品質要素から分割境界を動かすことを失敗することがあります。これはZoltanが低品質要素よりも負荷バランスを優先し、負荷バランス条件のために低品質要素が無視されるのが理由です。解決策としてZoltanパラメーターIMBALANCE_TOLを緩めることとしました。

Zoltanでは、良い負荷バランスの領域分割が優先されます。負荷分散の許容値はIMBALANCE_TOLで制御されます。各プロセッサー上の分散を見るためには、割り当てられたオブジェクト全てのウェイトの総和を取り、総負荷を計算します。これを用いて平均負荷を計算し、負荷分散は最大負荷を平均負荷で割って算出できます。例えばIMBALANCE_TOLが1.2であれば、負荷分散が20%まで許容できるという意味になります：つまり平均負荷の1.2倍以上の負荷を持つプロセスは実行されません。

デフォルトのIMBALANCE_TOLは1.075としましたが、Fluidityでは1.5に変更されていました。このオプションはFluidityオプションシステムのload_imbalance_toleranceを用いて変更可能です。ユーザーは自身の問題に適用可能なように値を変更できます。こうして低品質要素がハロ領域に残る問題は解決しましたが、これは空領域の問題を生じます。

IMBALANCE_TOLを緩めると、Zoltanはしばしばプロセスがその自身のノードを持たないようなやり方でメッシュを分割しようとします。Fluidityは空の領域を持つプロセスは存在しないことを仮定しますが、これはコード全体で様々な問題を引き起こします。空の領域を扱うようにFluidityを変更するのは現実的でなく、その代わりに空の領域を作らないようにする方法を実装しました。これは、最初に負荷バランスを行ってからデータマイグレーションを行うという異なるステップに実装を分けることで可能です。

解決策は、負荷バランスを行った後に、データマイグレーション実行前に空の領域をチェックすることです。空の領域のチェックは下記を判断することです：

\begin{eqnarray} N_o+N_i-N_e \neq 0 \tag{2} \end{eqnarray}

ここで、$N_o$は専有ノード数、$N_i$はインポート・ノード数、$N_e$はエクスポート・ノード数です。このチェックは、Zoltan_LB_Balanceが返す、このプロセスにインポートされるノード数およびエクスポートされるノード数を用いれば可能です。

もし負荷バランス実行後に空の領域が生じたならば、IMBALANCE_TOLを絞って負荷バランスを再度実行します。このやり方を空の領域が生成されなくなるまで、あるいはIMBALANCE_TOLが絞れなくなるまで続けます。最終的な負荷バランスは、edge weightingを止めて、IMBALANCE_TOLを1.075にした場合に実行できました。これにより空の領域は生成されず、このプロセスをデータマイグレーション前に実行することにより、計算コストは削減されます。

３．３　データマイグレーション

Fluidityは3回Zoltan_Migrateを呼出します。その各々はノードと、ハロノードおよび場という異なるデータセットをマイグレーションします。この呼出しの各々に対して、コールバックの異なるセットが、送信すべき異なるデータをパック/アンパックするために用いられます。3つのコールバックが各Zoltan_Migrate呼出しについて必要です：

1.	各グラフノード(メッシュ・ノード、メッシュ・ハロノードあるいは要素の場データ)の保存容量
2.	Fluidityデータ構造からZoltan通信バッファへデータをパックする方法
3.	Zoltan通信バッファからFluidityデータ構造へデータをアンパックする方法

Zoltan通信バッファはバイト型配列です。これは、互いに直接データを転送することはできますが、Fluidityデータはほとんどが実数のため、そのデータ構造を複雑にします。やり方を簡潔にするために、場のデータを扱う場合は、実数配列をパック/アンパックに用いる事とします。パッキング・ルーチンでは、そのデータは最初にFluidityデータ構造からZoltan通信バッファへデータをパックされます。ここではFortranの内部手続きによる転送を用いて、パックされた実数データを整数のZoltan通信バッファへコピーします。アンパック時には、データは最初に整数Zoltan通信バッファから実数配列へコピーされた後に、実数配列からFluidityデータ構造へアンパックします。

３．４　ディテクター

ディテクターは流れに投げ込まれた粒子(ラグランジュ・ディテクター)あるいは流れ中の静的プローブを意味します。ラグランジュ・ディテクターは、混相流の計算を含む様々なアプリケーションや個人ベースの生物学的モデリングのエージェントとして用いられます。これらは共に、流体中に膨大な数のディテクターを用います。並列アダプティビティ実行においては、ディテクターは、Zoltanが、要素が新しいプロセッサーへ転送されるとみなす場合には、その要素に属して動くべきです。

Zoltanの実装では、ディテクターは場のデータのマイグレーションを行うコールバック関数で扱われます。この理由は、各ディテクターがノードよりも要素に関係しているためであり、場の転送ステージまでにどのプロセスが各ディテクターを所有するか解らないためです。Zoltanの利用の前後で、場のデータの更新や、"稀な"ケース(corner case)に関しても実装が必要です。

ディテクターはFortran派生型として、座標、名前、要素、型、id等の全ての情報を持つものとして実装されます。またZoltan用に、派生型/実数バッファ間のディテクター情報をパック/アンパックするためのルーチンを実装します。 元々これらはZoltan 内部でのみ使用されていましたが、ディテクターがプロセッサー間で転送されるかどうかにかかわらず、その使用はユーザーに任されることになります。

場が転送される前に、ディテクターリストは前処理で事前に生成すべきです。これにより、ディテクターはその前処理で、一つあるいは複数の順序なしリンクリストに保存されるため、パッキング・コールバック中のリストの検索が不要になります。この前処理は、場のデータサイズを決めるコールバック関数からのサブルーチン呼び出しとして実行されます。この前処理は、プロセスから転送される要素リストが利用可能になる、まさにこの時点で実行されます。この前処理は以下のように構成されています：

1.	各ディテクターが属する要素を決める
2.	ディテクターの要素が転送される場合には、現状のディテクターリストから送り先のディテクターリストへ、そのディテクターを移す /td>
3.	転送される各要素についてディテクター数を維持する

以下の疑似コードはこの3ステップの実装を示しています：

Listing2 : Detector re-distribution

for list = 1 to # detector lists
　for detector = 1 to # detectors in list
　　Determine element the detector is associated with
　　for element = 1 to # elements being transferred
　　　Determine elementu niversal number
　　　if(detector element = element universal number)
　　　　Determine new element owner
　　　　if(new element owner = current element owner)
　　　　　Do not need to transfer the detector
　　　　else
　　　　　Move detector to list of detectors to pack
　　　　　Increment number of detectors in the element

この実装はディテクターリストを一回より多く転送しないことを狙ったものです。各ディテクターは、もしそれが属する要素が転送対象となった要素のリストに在る場合のみチェックされます。もしそうであれば、その要素を所有するプロセスが新しい領域分割において決定されます。もし新しい所有者が現状のものであるならば、その要素は、別のプロセス内の新しい領域分割におけるハロであるとして、データ転送のみ実行されます。Fluidityではディテクターは、そのディテクターを含む要素を所有するプロセスによってのみ扱われるため、ハロ要素においてディテクターは転送されません。もし新しい所有者が現状のものでないならば、新しい領域分割において要素の帰属が変更され、ディテクターは転送されなければなりません。そのディテクターは、現状のディテクターリストから転送先のディテクターのリストへ移され、その要素内のディテクター数が一つ増やされます。

ディテクターリストの前処理は、転送される各要素内のディテクター数を含む配列と、転送されるディテクターの順序リストを生成します。ディテクターが送信ディテクターリストへ追加される順序は、通信バッファへパックされる場合にリストから外される順と同じです。よってこの前処理により、送信ディテクターリストはパッキング処理中に順番にスキャンされ、転送されるべきディテクターを送信ディテクターリストで検索する必要は生じません。

コールバック関数の以下の修正により、Fluidityの並列アダプティブ・シミュレーションへディテクター機能が追加されました：

1.	場のデータサイズ・コールバック中に、ディテクターリストの前処理を行います。このコールバックは、前処理場で計算された各要素のディテクター数を用いて、場のデータと共にディテクター情報の全てをパッキングするのに十分なメモリー確保を確実なものにします。
2.	場のデータのパッキング・コールバック中には、各要素に対して、要素内のディテクター数のループが走り、送信ディテクターリストからディテクターを抜き出して通信バッファ内へパックします。
3.	場のデータのアンパッキング・コールバック中には、各要素に対して、送信されたディテクター数を読み込みます。転送されたディテクター数のロープが走り、それが新しい領域分割における自身のプロセスが所有するものかどうかをチェックします。もし所有するのであれば、新しいディテクターをアンパックされたディテクターリストにアロケートして、ディテクターのデータをその中にアンパックします。

場のデータのアンパック・コールバックにおけるディテクターのアンパック処理では、一時的なアンパック・ディテクターリストが用いられます。これはマイグレーション後に用いられ、転送されなかったディテクターは、転送されたディテクターへのマージ前に、通常のリスト内で更新できます。要素はマイグレーション時には複数のプロセスへ転送されます。ディテクターをアンパックする際に、各プロセスはディテクターの要素の帰属をチェックし、それが新しい領域分割におけるその要素の所有者であるならば、アンパック・ディテクターリストへアンパックのみ行います。

以上のようにZoltan_Migrateが呼び出されて場のデータが転送されたら、転送されなかったディテクターを含むディテクターリストは更新されなければなりません。ローカル要素番号は新/旧の領域分割間で変化し、各ディテクターは特定のローカル要素番号と関連するので、この値は更新されなければなりません。これは2つのマッピングを用いて行われます：

• 旧ローカル要素番号と、データマイグレーション前に旧メッシュから生成されたユニバーサル要素番号の間
• ユニバーサル要素番号と、ノードマイグレーションおよび新しいメッシュ構築後に新しいメッシュから生成された新ローカル要素番号の間

各ディテクターは、最初にユニバーサル要素番号、次にユニバーサル要素番号から新ローカル要素番号へマップされた要素の要素番号を持ちます。新ローカル要素番号はディテクターに保存されます。

ディテクターのマイグレーションにおいてさらに困った事が生じます。この"稀な"ケースは、前処理で転送された要素内にディテクターが在るところで、その要素が新しい領域分割の現状所有プロセスに属さない場合に生じます。この場合、そのディテクターを、他のプロセッサーが所有する要素内にそれが在ることを許諾するまで、それらへブロードキャストします。

最終的にディテクターリストが更新されれば、場のデータがマイグレーションされる際に、これらディテクターをアンパック・ディテクターリストから受け取ります。アンパック・ディテクターリスト内の各ディテクターは、ユニバーサル要素番号を付加された要素所有者へ転送されます。ユニバーサル要素番号は新しい新しいローカル要素番号へマッピングされ、ディテクターの要素所有者は更新され、ディテクターはアンパック・ディテクターリストから適切なディテクターリストへ移動させられます。

３．５　flredecomp

Zoltanは、Fluidityに提供されているツールflredecompでも利用されています。このツールは複数プロセスで入力チェックポイントを新しいチェックポイントへ再構成するツールです。アダプティブ・シミュレーションにおいて要素数は変化しますが、要素数がメモリー容量を超えてしまうことがあります。この場合にはチェックポイントを行い、より大きな領域分割数へ変更し、リスタートすることが可能です。このツールはストロング・スケーリング(強スケーリング、strong scaling)性能の改善にも有用です。

FlredecompでZoltanを用いる場合に、アダプティビティからも同様のコードが呼ばれますが、論理型flredcompingを真に設定しています。これはzoltan_driveの様々なオプションを変化させます。その領域分割は、負荷バランスの最終領域分割での一回の繰り返しのみを実行する際に用いる、均一なedge-weightingで実行されます。

Flredecompから呼ばれる場合には実装には、Zoltan LB BalanceではなくZoltan LB Partitionを用いて、その場合にのみZoltanパラメーターNUM GLOBAL PARTSとNUM LOCAL PARTSを使用します。これらは全プロセスに対して設定すべきで、全プロセッサーに対して同じNUM GLOBAL PARTS値を、また各プロセッサーに個別にNUM LOCAL PARTSを用います。NUM GLOBAL PARTSはZoltanに生成すべき領域総数を伝え、NUM LOCAL PARTSはZoltanに、特定のプロセスへ配置すべき領域数を伝えます。Zoltan LB BalanceはZoltan LB Partitionの特定バージョンというもので、そこではNUM GLOBAL PARTSは実行プロセス数、NUM LOCAL PARTSは全プロセスに対して1とします。flredecomp でのNUM GLOBAL PARTSは、チェックポイントを再構成する時使用するプロセス数です。スケールアップ時にはNUM LOCAL PARTSは全プロセスに対して1ですが、スケールダウン時には、ターゲットプロセス数分は1で、それ以外は0とします。

４．　性能プロファイル

Fluidityの一般的なユースケースを1例題ベンチマークとして実行してみました。これは、区間線形連続ガラーキン法の離散化(P1P1)を用いた後方ステップ流れCFD計算の例です(図4)。この離散化は、CFDにおいて一般的な選択であり、Sam Gormanによるコード(以降Samと略記します)であるベースラインとの比較も可能です。この他のベンチマークは、アダプティブでないもの、あるいはアダプティブが可能でSamの手法が実行できないものを採用しました。

図4 ：　後方ステップ流れ(上図)のトレーサー場、および領域分割境界を赤線で示したアダプティブメッシュ(下図)のスナップショット。

残念ながらHECToR上のプロファイリング実行において、Zoltanを通してParMETISを用いる事が出来ませんでした。この実行は以前は可能でしたが、Zoltan3.5のバグらしき事象が見出されました。この原因は、Zoltanのドキュメントからは本来不要なはずの追加のコールバックが要求されることでした。この問題はZoltanの開発者により明らかになりました。Zoltan3.4では実行可能だったこの問題は、近い将来に解消されると考えられます。

同じくZoltanを通してPT-Scotchを用いた場合、16プロセッサー以上でプロファイルを採取することが出来ませんでした。これは、PT-ScotchがHECToRシステム上で1コア以上を使用した場合にMPIエラーを生じるためです。この問題はHECToRシステムのバグであることが明らかになりました。

以下に示すプロファイル結果は、HECToRフェーズ3システムでの実行結果です。これは総数2816のXE6計算ノードで構成されるCray XE6システムです。各計算ノードは2つのAMD 2.3GHzの16コアプロセッサーから構成され、総コア数は90,112コアです。このことから、理論ピーク性能は800 Tflopsを超えます。ノード当たり32GBのメインメモリーを持ち、総メモリー容量は90TBです。プロセッサーは、Cray Gemini通信チップによる高バンド幅インターコネクトで結合されています。Geminiチップは3次元トーラス上に配置されています。

図5から10は、HECToR上での後方ステップ流れの小規模ベンチマークのプロファイル結果を示しています。これは、32-64プロセッサーを用いる場合の典型的な、約23,000要素を使った小規模ベンチマークです。別の領域分割手法をテストするために、256プロセッサーまでのテストを行いました。さらに、通常良く用いられる10や20ステップではなく、2ステップ毎にメッシュの動的アダプティビティを実行しました。こうすることで、アダプティブ・アルゴリズムがこれらベンチマークの主要な計算時間を占めることとなります。多くの問題ではこうした状況にはならず、流れを構築して解く部分が実行時間を支配します。

図5では、Zoltan実装とベースラインSamは8プロセッサーまでは同等の性能を示します。8プロセッサーを超えると、Zoltanの実行時間はSamより多くなっています。

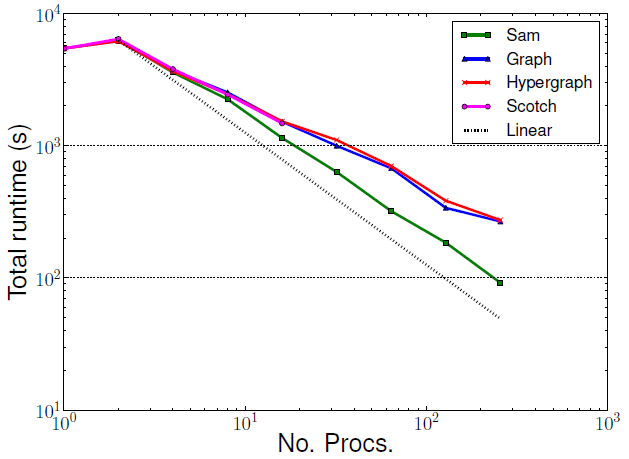
図5 ：　小規模後方ステップ流れベンチマークの全実行時間

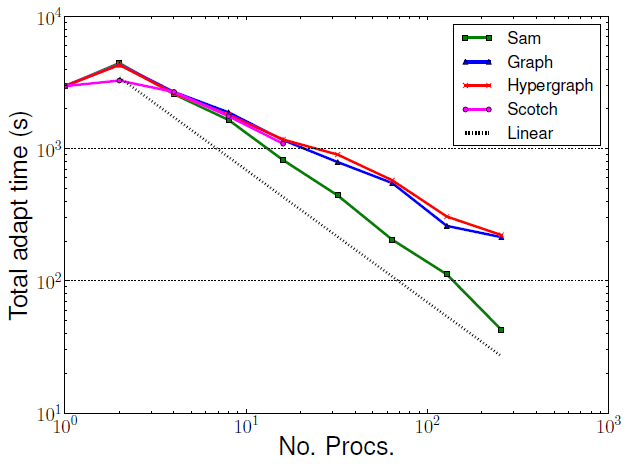
図6 ：　小規模後方ステップ流れベンチマークの全アダプティビティ実行時間。全アダプティビティ実行時間の増加が全実行時間へ反映している。

これはZoltanを用いたアダプティビティ実行時間の増加が原因です。Zoltanは一般用途向けであるため、Zoltanによるアダプティビティ実行がSamよりも時間が掛かるのは予想されることです。Samは特定の要素タイプのみを用い、場のデータをノードへ同時にマイグレーションすることを可能にしています。Zoltanは場のデータのために追加のマイグレーション・フェーズを用いています。図10は、領域分割の負荷が高い場合に、この追加のマイグレーションがZoltanの性能に影響を与えることを示しており、これは小規模問題を必要以上に多くのプロセッサーに分割する場合と同じ状況です。同様な時間増加はシリアル実行では見られません(図9)。

別の領域分割手法、特にハイパーグラフがフェーズ計算部分の負荷バランスを改善して、このコード部の性能を向上させることが期待されます。ですが、図7，8が示すように、フェーズ計算部に性能改善は見られませんでした。

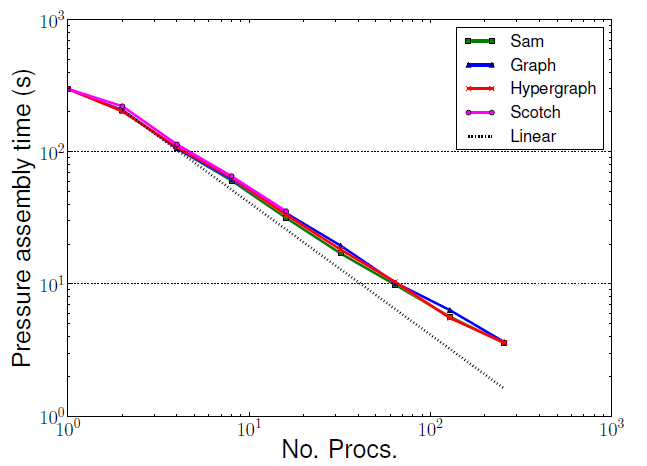
図7 ：　小規模後方ステップ流れベンチマークの圧力生成実行時間

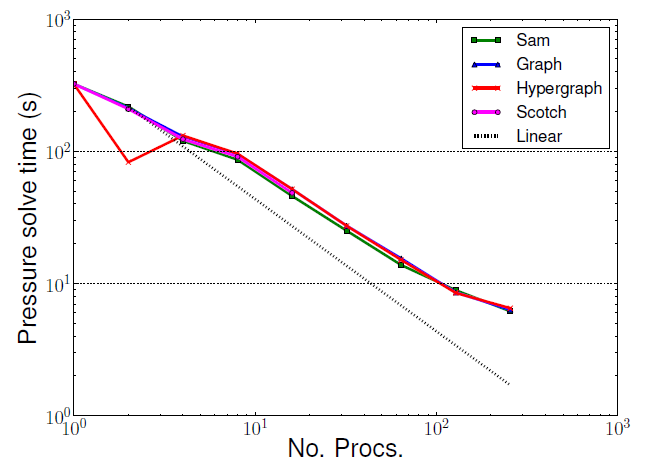
図8 ：　小規模後方ステップ流れベンチマークの圧力求解実行時間

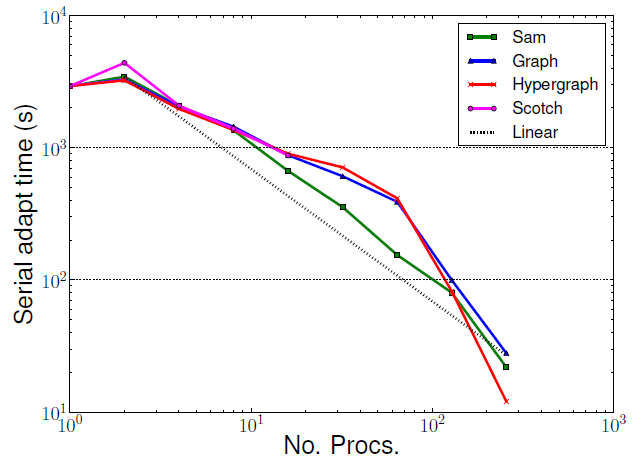
図9 ：　小規模後方ステップ流れベンチマークのシリアル実行時間

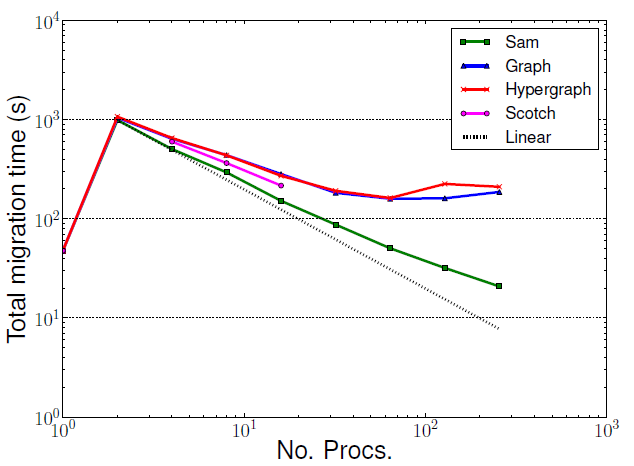
図10 ：　小規模後方ステップ流れベンチマークの全マイグレーション実行時間

５．　結果

本作業は性能向上だけでなく、メンテナンス性や拡張性および再分割の機能性も向上させることが目的でした。新しいZoltanを用いた実装は、並列周期問題を解くように拡張されました。ディテクターは並列アダプティブ・シミュレーション内に実装されました。Zoltanの機能的な優位性は、それが一般用途向けであることです。それは、並列アダプティブ・シミュレーションにおいて如何なる要素タイプも扱うことが出来ます。これによりFluidityは、以前に扱うことが出来なかった新しい科学に対して用いることが可能になりました。例えば、泡のモデリングはP0P1離散化とアダプティブメッシュにより可能です(Brito-Parada et al., 2011)。これをシリアル実行するのは現実的でなく、Zoltanを組込むことにより新しい科学計算が可能になりました。

本作業の詳細は、HECToR dCSE Technical Workshop on 4th and 5th October, 2011において発表され、資料はhttp://www.hector.ac.uk/cse/distributedcse/technical2/から閲覧可能です。

６．　謝辞

このプロジェクトは、NAG Ltd.が運営するHECToRの分散計算科学および工学(CSE)サービスの基に実行されました。英国の国立スーパーコンピューティング・サービスである、HECToR：英国リサーチ・カウンシル・ハイエンド計算サービスは、リサーチ・カウンシルを代行するEPSRCが管理しています。そのミッションは英国学術界の科学および工学の研究支援です。HECToRスーパーコンピューターは、UoE HPCx Ltd.およびNAG Ltd.のCSEサポートサービスにより管理運営されています。

文献

[1]	Babuška, I., Suri, M., 1994. The p and h-p versions of the Finite Element method, basic principles and properties.SIAM Review 36, 578.
[2]	Berger, M.J., Colella, P., 1989. Local adaptive mesh refinement for shock hydrodynamics. Journal of Computational Physics 82, 64-84.
[3]	Boman, E., Devine, K., Fisk, L.A., Heaphy, R., Hendrickson, B., Vaughan, C., Catalyurek, U., Bozdag, D., Mitchell, W., Teresco, J., 2007. Zoltan 3.0: Parallel Partitioning, Load-balancing, and Data Management Services; User's Guide. Sandia National Laboratories. Albuquerque, NM.
[4]	Brito-Parada, P., Neethling, S., Cilliers, J., 2011. The advantages of using mesh adaptivity when modelling the drainage of liquid in froths. Minerals Engineering , Corrected proofs.
[5]	Budd, C.J., Huang, W., Russell, R.D., 2009. Adaptivity with moving grids. Acta Numerica 18, 111-241.
[6]	Catalyurek, U.V., Boman, E.G., Devine, K.D., Bozda, D., Heaphy, R.T., Riesen, L.A., 2009. A repartitioning hypergraph model for dynamic load balancing. Journal of Parallel and Distributed Computing 69, 711-724.
[7]	Davies, D.R.,Wilson, C.R., Kramer, S.C., 2011. Fluidity: A fully unstructured anisotropic adaptive mesh computational modeling framework for geodynamics. Geochem. Geophys. Geosyst. 12.
[8]	Devine, K., Boman, E., Heaphy, R., Hendrickson, B., Vaughan, C., 2002. Zoltan data management services for parallel dynamic applications. Computing in Science and Engineering 4, 90-97.
[9]	Farrell, P., 2009. Galerkin Projection Of Discrete Fields Via Supermesh Construction. Ph.D. thesis. Imperial College London.
[10]	Farrell, P., 2011. The addition of fields on different meshes. Journal of Computational Physics 230, 3265 - 3269.
[11]	Farrell, P.E., Piggott, M.D., Pain, C.C., Gorman, G.J., Wilson, C.R., 2009. Conservative interpolation between unstructured meshes via supermesh construction. Computer Methods in Applied Mechanics and Engineering 198, 2632-2642.
[12]	Gorman, G., 2006. Parallel Anisotropic Unstructured Mesh Optimisation And Its Applications. Ph.D. thesis. Imperial College London.
[13]	Ham, D.A., Farrell, P.E., Gorman, G.J., Maddison, J.R., Wilson, C.R., Kramer, S.C., Shipton, J., Collins, G.S., Cotter, C.J., Piggott, M.D., 2009. Spud 1.0: generalising and automating the user interfaces of scientific computer models. Geoscientific Model Development 2, 33-42.
[14]	Hiester, H.R., Piggott, M.D., Allison, P.A., 2011. The impact of mesh adaptivity on the gravity current front speed in a two-dimensional lock-exchange. Ocean Modelling 38, 1-21.
[15]	Houston, P., S¨uli, E., 2001. hp-Adaptive discontinuous Galerkin finite element methods for first-order hyperbolic problems. SIAM Journal on Scientific Computing 23, 1226-1252.
[16]	Ledger, P.D., Morgan, K., Peraire, J., Hassan, O., Weatherill, N.P., 2003. The development of an hp-adaptive finite element procedure for electromagnetic scattering problems. Finite Elements in Analysis and Design 39, 751-764.
[17]	Mitchell, A.J., Allison, P.A., Piggott, M.D., Gorman, G.J., Pain, C.C., Hampson, G.J., 2010. Numerical modelling of tsunami propagation with implications for sedimentation in ancient epicontinental seas: The lower jurassic laurasian seaway. Sedimentary Geology 228, 81 - 97.
[18]	Pain, C., Piggott, M., Goddard, A., Fang, F., Gorman, G., Marshall, D., Eaton, M., Power, P., de Oliveira, C., 2005. Three-dimensional unstructured mesh ocean modelling. Ocean Modelling 10, 5-33.
[19]	Pain, C.C., Umpleby, A.P., de Oliveira, C.R.E., Goddard, A.J.H., 2001. Tetrahedral mesh optimisation and adaptivity for steady-state and transient finite element calculations. Computer Methods in Applied Mechanics and Engineering 190, 3771-3796.
[20]	Piggott, M.D., Farrell, P.E., Wilson, C.R., Gorman, G.J., Pain, C.C., 2009. Anisotropic mesh adaptivity for multi-scale ocean modelling. Philosophical Transactions of the Royal Society A 367, 4591-4611.