Lucian Anton, Numerical Algorithms Group Ltd.
本レポートはコードCASINOに対する1年に渡るdCSEサポートプロジェクトの成果を示したものであり、i)同一プロセッサーのタスク間で共有データを用いたメモリー効率の向上と、ii)第2レベルの並列化実装による計算速度向上、およびiii)大規模初期データ入力速度の向上に焦点を当てています。
目次
1 イントロダクション
1.1 背景
1.2 変分モンテカルロ(VMC)
1.3 拡散モンテカルロ(DMC)
1.4 CASINOの概要と課題
2 大規模データセットの共有
2.1 プロセッサー/ノード上の共有メモリー(SHM)
2.2 MPI双方向データ転送(MPI-2S)
2.3 片方向データ転送(MPI-1S,SHMEM)
2.4 テスト結果
3 MPIによる第2レベル並列化
4 OpenMPによる第2レベル並列化
5 データ入力の最適化
6 結論
1 イントロダクション
1 背景
量子モンテカルロ(QMC)法は、結晶、ナノクラスターあるいはマクロ分子のような比較的原子数の多い物理系の性質を計算するための、高精度な数値計算ツールです。QMCの計算時間はシステムサイズの2乗から3乗に比例するという利点がありますが、正確な結果を出すには多数の位相空間配位数が要求され、QMC問題を解くには最も効率の高いハードウェアとアルゴリズムが必要となります[1]。
用語の整理のために、以下においてQMCアルゴリズムの基礎のための数学的概念を簡単に記述します。より詳細には参考文献[3,4]を参照してください。
典型的な量子多体系は、位置$\mathbf{R}={\vec{r}_e}$の$N_e$個の電子、これらは$N_↑$個の上向きスピンと$N_↓=N_e-N_↑$個の下向きスピンから成り、および位置$\mathbf{R}_I={\vec{r}_I}$の$N_I$個のイオンを持ちます。粒子間相互作用は以下の量子力学的ハミルトニアンで記述されます:
\begin{eqnarray} H=-\sum_{i=1,N_e} \frac{\hbar^2}{2m} \nabla^2_{r_i}+V(\mathbf{R},\mathbf{R}_I) , \end{eqnarray}
その固有状態と固有値から、原理的には系を記述する全ての物理量を求めることが出来ます。現実的なハミルトニアンでは正確な解を得ることは困難ですが、一粒子近似を基に良好な物理的結果が得られ、この種の最も成功したテクニックとして密度汎関数理論(DFT)があります。
QMC計算は、次に述べる2つのQMC法を用いて一粒子解へ電子相関の寄与を与えることにより改善されます。
1.2 変分モンテカルロ(VMC)
VMCは試行関数$\Psi(\alpha,\mathbf{R},\mathbf{R}_I)$を用いて、そのパラメーター$\alpha$を下記のエネルギー平均の最小化あるいは変分から決定します:
\begin{eqnarray} E(\alpha)=\frac{\langle\Psi(\alpha)|H|\Psi(\alpha)\rangle}{\langle\Psi(\alpha)|\Psi(\alpha)\rangle}. \tag{1} \end{eqnarray}
電子系の典型的な試行関数は、DFT計算から得られた一粒子軌道(OPO)のスレーター行列式の積で、電子相関を記述する関数を掛けたものです。
\begin{eqnarray} \Psi(\alpha,\mathbf{R},\mathbf{R}_I)=e^{J(\alpha,\mathbf{R},\mathbf{R}_I)}D_↑(r_1,…,r_{N_↑}) \tag{2} \\ \times D_↓(r_{N_↑+1},…,r_{N_e}), \tag{3} \end{eqnarray}
ここで$D_↑,↓$は上向きスピン(↑)と下向きスピン(↓)の電子に関するスレーター行列式です。最も簡単なJastrow因子$J(\alpha,\mathbf{R},\mathbf{R}_I)$は2電子関数の和です。
\begin{eqnarray} J(\alpha,\mathbf{R},\mathbf{R}_I)=-\sum_{i>j,\sigma_i,\sigma_j}u_{\sigma_i,\sigma_j}(\alpha,|r_i-r_j|) \tag{4} \end{eqnarray}
ここで$u$は一様電子ガスのものを取ります。これまでより高度な$J(\alpha,\mathbf{R},\mathbf{R}_I)$が、3電子相関や電子イオン相関を取り込むために研究されてきました[4]。
多くの研究により、VMCはその相関エネルギーの70から90%を取り込むことが明らかになっていますが、VMCの枠組みで残りの寄与を系統的に改善することは困難である事が示されてきました。CASINOにおいてVMCを用いる主な目的は、拡散モンテカルロ計算で必要となる配位を生成することです。
1.3 拡散モンテカルロ(DMC)
DMC法は、下記の虚数時間$t=i\tau$でのシュレディンガー方程式が、ポテンシャルによる分岐/消滅項を付加した拡散方程式と見做せるという事実に基づいています。
\begin{eqnarray} -\frac{\partial \Psi(\mathbf{R},\tau)}{\partial \tau}= -\frac{1}{2}\nabla^2\Psi(\mathbf{R},\tau) +(V(\mathbf{R})-E_T) \Psi(\mathbf{R},\tau) \tag{5} \end{eqnarray}
パラメーター$E_T$を基底状態エネルギーに最適化出来れば、試行関数はハミルトニアンの基底状態に射影されます。電子の波動関数の反対称性は式(5)を解く際に深刻な問題を生じます。この問題を避けるために、節固定近似(fixed-node approximation)と呼ばれる手法を用いて式(5)を変形し、波動関数を試行関数と同じ節面を持つ基底状態波動関数へ射影します。実際の計算はこれが非常に良い近似であることを示しています。
1.4 CASINOの概要と課題
CASINOは過去10年以上に渡り、キャベンディッシュ研究所において開発・維持されて来たQMCソフトウェアパッケージです[2,3]。
CASINOのQMCアルゴリズムは、配位として$N_e$個の3次元ランダムウォーカー(RW)を用いており、RWはVMC計算式(1)の試行関数、あるいはDMC計算式(5)に関連付けられた分布確率に従って計算されます。
典型的な計算は主に以下のステップで進みます:
- 軌道関数係数やJastrowパラメータなどの入力パラメーターと入力データを読み込む
- VMC計算を実行し、DMC計算で必要なRW配位を生成する
- DMC計算を実行する: 配位の変更を試し、ローカルエネルギーを計算して分岐を決定し、物理量の統計値を計算する
- もし並列で計算をするならば、計算量を均一に分散するためにタスク間の配位の再配置を行う
モデルに含まれる電子数の関数として与えられるCASINOの性能を決定するのは主に、2つあります:i)モンテカルロ・アルゴリズムで軌道を格納するメモリー量、およびii)電子数に対する計算時間のスケーラビリティーです。
これとは別に実用面において、1000電子以上を含むモデルの並列計算、および5000タスク以上の計算において、軌道データや事前に保存された配位データを読み込むのに、極めて長い時間が掛かっていました(30分から60分)。
本レポートの以降のセクションでは、上述の問題に対する解決策の詳細を説明し、それがコードに与える性能上の利得について議論します。セクション2ではOPOデータの共有アルゴリズム、およびそれら各種アルゴリズムの性能測定値を示します。セクション3,4では第2レベル並列アルゴリズムを示し、その性能を解析します。セクション5では初期データ入力の改善策を示します。HECToRフェーズIのデュアルコアAMD Opteronと、HECToRフェーズIIのクアッドコアAMD Opteron上でベンチマークを実行しました。デュアルコアプロセッサーの仕様は、クロック2.8 GHz、6GB RAM、64KB L1 cache、1MB L2 cacheで、倍精度のピーク性能は11.2Gflopsです。クアッドコアプロセッサーの仕様は、クロック2.3 GHz、8GB RAM、64 L1 cache、512KB L2 cache、2MB L3 cache(shared)で、倍精度ピーク性能はほぼ40Gflopsです。コードはPGI v8.0でコンパイルしました[2,6]。
2 大規模データセットの共有
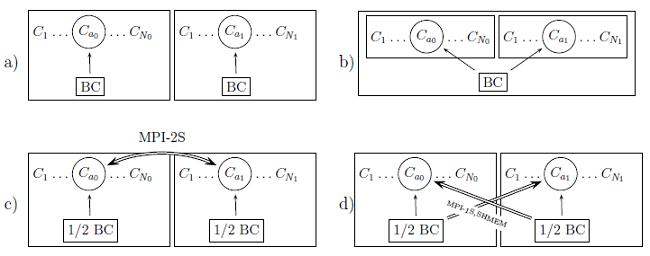
図1 : 各種アルゴリズムでの2タスクのBCデータアクセスパターン。各タスクは格納されたBCを用いて配位$C_1,…,C_{N_t}$をシリアルモードで計算する:a)標準バージョンでは各タスクは自身のBCデータを保持する、b)BCデータは共有メモリーの1セクターに置かれる、c)MPI双方向バージョン:BCデータはMPI双方向通信で転送される、d)MPIあるいはSHMEMで実装された片方向転送。
本セクションでは図1に示した軌道データ共有の3手法について説明します。
CASINOの計算は一度に1つのランダムウォーカーを進行させ、各ステップでの遷移確率は、全ランダムウォークの現在位置におけるJastrow因子とOPOの現在値に依って決定されます。軌道は平面波や、ガウシアン、あるいはB-スプライン等を用いた基底関数で表現されます。本レポートではB-スプライン表現[5]を使用します。これは全物理系を含む実空間内における3次元グリッド上の局所的な3次多項式です。これはシステマチックに改善可能で如何なるバイアスも無いという平面波と同じ性質を持ちますが、局所化されており、かつ平面波より$1/N_e$分効率が良いものです:空間の各点では常に、非零値を持つB-スプラインは64個だけ存在します。よって各軌道の計算は64個のB-スプラインのみで可能で、これは電子を多数持つ系の平面波の総数よりもかなり小さな数です(平面波の数は$N_e$に比例します)。
プログラム内ではB-スプライン係数(BC)は5次元配列$a(1:N_b;0:N_{gx}-1;0:N_{gy}-1;0:N_{gz}-1;N_s),$に格納されており、ここで$N_b,N_{gx},N_{gy},N_{gz},N_s$はそれぞれ、軌道数、3次元空間のグリッド数、およびスピン数です。
計算で必要となるBCの量は2つの要因で決定されます:i)各スピンに対して、軌道数はそのスピンをもつ電子数と一致しなくてはならない、ii)グリッド間隔はOPOを求めたDFT計算の精度で決定され、その精度が高ければグリッドもより高解像であるべきです。
上述の要求は膨大なBCデータを要請します。例えば、上向きと下向きスピンが半数の1000電子の系を考えると、非磁気系であれば両方のスピンに同じBCセットを用いることが出来るため、500の電子軌道が必要となります。空間のグリッドは各方向に80点以上に及び、BC値を倍精度で確保するとすれば全体で2GBメモリーに達して、HECToRで用いるプロセッサーのコア当たりの最大メモリーにほぼ匹敵します。
当初のCASINOのアルゴリズムでは、軌道計算に必要なBCのコピーを各タスクが持つ仕様でした。BCのセットは各タスクで同等でありその値は計算中に不変なため、タスクグループ間でデータを共有することで、共有メモリーを実装するマシンであればなおのこと、メモリー問題は解消できます。
2.1 プロセッサー/ノード上の共有メモリー(SHM)
本校作成時にはMPI標準は、共有メモリーシステムのタスクグループにコモンメモリーセグメントをサポートする可能性に言及していませんでした。ですが、共有メモリーはUnix System Vの内部プロセス通信関数shmgetとshmat[7]により利用可能で、これら関数はメモリーセグメントをアロケーションし、各タスクのメモリー空間に追加することが出来ます。
このアルゴリズムのステップは以下のようなものです:
- "mpi get processor name"を用いて同じプロセッサーやノード(メモリーを共有する複数プロセッサー)に有るタスクを検出する
- BCの確保に必要なメモリーをアロケーションして、それをshmgetとshmatを使ってタスクメモリーへ追加する
- Cray pointerを介して共有メモリーセグメントの参照をFORTRANプログラムへ渡す
これは、共有メモリーを使うことが可能なタスクを分類して、それらのために共有メモリーセグメントを生成するC言語の関数群を使用して実装します。Cray pointerを用いてFORTRANポインターへ共有メモリーを利用可能にするサブルーチンは、FORTRANモジュール[6]で提供されています。
CASINOのFORTRAN95+MPIという標準的なコーディング実装の中で、2点ポーテビリティに欠ける部品があるとすれば、現状で広く並列マシンで利用されてはいますが、一つは全OSに対してポータブルでない共有メモリー関数と、もう一つはFORTRAN95規格でないCray pointerです。
CASINOのポータビリティの要請あるいは共有メモリーを使用しない場合に答えるために、当初のアルゴリズム、つまり各タスクがBCのコピーを持つアルゴリズムを実装した別のFORTRANモジュールも用意されました。ユーザーはmakefile変数として2つのモジュールを切り替えることが出来ます(CASINOはコード・プリプロセッサーを使用しません)。
2.2 MPI双方向データ転送(MPI-2S)
このアルゴリズムは2008年にLLNLのRandolf HoodによりCASINOへ実装されました。本レポートではこれを性能試験で用いるため、その主な特徴をここで記します。このアルゴリズムはタスク間のBCデータ転送に対して双方向MPI関数呼出しを用います。主なステップは以下の通りです:
- 全タスク数を$n_g$サイズのグループに分割する
- 各タスクは全区間グリッドと周期条件でピックアップされた$N_g/n_g$個の軌道を持つという条件において、各タスクグループへBCデータを分配する
- あるタスクが与えられた電子の軌道の計算を必要としたら、そのタスクは電子の座標をグループメンバーへブロードキャストし、BCデータが各タスクで格納されて軌道計算値が戻ってくるまで待機する
各タスクはその配位をランダムに動かすため、同期の仕組みが必要になります。現状の実装では、配位計算の内側ループで関連のタスクから軌道計算の要請に答える監視機能を追加しています。
2.3 片方向データ転送(MPI-1S,SHMEM)
これはMPI-2Sのバリエーションの一つで、MPIやSHMEMライブラリーによる片方向データ転送を使って、上述のアルゴリズムの同期の遅延を回避する試みです。この場合、軌道計算部に到達したタスクはBCデータセットにアクセス可能で、それは関連するタスクのメモリーから求めますが、対応する側での関数呼出しは不要です。このアルゴリズムは2つの欠点があります:i)2タスク間のデータ転送量は軌道の転送に比べて64倍になります、ii)転送されるデータセットが4×4×4ブロックの空間グリッドであることからメモリーアドレスの連続性が失われます。
2.4 テスト結果
表1はここで議論したアルゴリズムによる軌道計算ルーチンの実行時間を示しています。そのデータは短い実行(12時間ステップ)から収集しましたが、それはDMCセクションのコードの内部タイマーにより1000時間ポイントに及びました。DMCの全実行時間も示されています。この系は1024電子から成り、そのBCデータサイズはほぼ2.4GBです。
| CPU | 2DC | 4DC | 4QC | |||
| OPO | DMC | OPO | DMC | OPO | DMC | |
| SHM | 130 | 921 | - | - | 139 | 882 |
| MPI-2S | 371 | 1184 | 806 | 1458 | 546 | 1249 |
| MPI-1S | 562 | 1380 | 1669 | 2565 | 1430 | 2210 |
| SHMEM | 210 | 975 | 771 | 1759 | 536 | 1271 |
期待通りに、SHMアルゴリズムは不要なタスク間のデータ転送が無いので、断然に最高効率を示しています。MPI-2Sは、データ量が共有メモリーを超える場合(幾つかの不規則系の場合に発生します)に選択肢となり得るでしょう。MPI片方向通信の性能劣化についてDavid Tanquerayは次のように述べています:一見片方向MPIは非同期のように思えますが、MPI標準ではそのような実装要請は一切なく、MPICH実装に置いては実際に、それらは全て蓄積された後に、引き続く収集あるいは同期呼出しで一斉に実行されており、内部的には双方向MPI通信の設計基盤の一部として扱われています。片やSHMEMは通常非同期に動作し、非同期サポートの一部を提供するXT Portalライブラリーで構築されたものであり、事実SHMEMの結果はMPI-2Sより少し良い性能を示しています。
3 MPIによる第2レベル並列化(SLP)
第2レベル並列(SLP)アルゴリズムは、一つのRW配位を次の状態に移すのにタスクを複数用いる事により、性能向上を図ります。CASINOの単一配位の実行時間は$p$を2か3とする$N_e^p$に比例するので、電子数$O(10^4)$の系では配位当たりの実行時間は、現状の計算としては最大サイズと考えられる電子数$O(10^3)$の系に比べて100倍以上時間が掛かかります。SLPは大規模BCサイズ問題を解決します。これはBCデータを一つの配位を実行するタスクグループ間に分配して並列計算の負荷バランスを改善します。何故なら異なるプールに有る配位数間の相対的な差がプールサイズ(タスクあるいはタスクプール毎の固定した配位数を持つ計算に対して)と共に減少するからです。
MPI-2Sの場合のように、SLPはタスクを与えられたサイズ(典型的には2か4)でグループ分けして、これをプールと呼びます。プログラムは最初にBCデータを読み込み、MPI-2Sと同様にそれらをプールメンバーへ分配します。違いは、プールに属する全てのタスクが単一の配位を計算することです。プールヘッドと呼ばれる一つのタスクは、計算を制御して、他のタスクへ計算の次のステップに関するシグナルを送ります。こうしてMPI-2Sでの同期の問題は回避され、プール内のタスクはより多くの量を並列に計算することが可能になります。これにはJastrow因子の総和や、ポテンシャルエネルギーや、スレーター行列式で必要な線形代数演算などの軌道計算も含まれます。
SLPアルゴリズムの性能を以下のように解析します:理想的にはプールサイズがnの場合は単一配位計算の時間は$t_n=t_1/n$になるでしょう。しかしながらタスク間通信時間は無視できません。その内容はタスク間に均等に分散されるわけではなく、プールヘッドのみで実行される計算も存在します。ここでプール利用効率を以下の指標で評価することとします:
\begin{eqnarray} \eta=\frac{t_1/t_n-1}{n-1} \tag{6} \end{eqnarray}
ここで$\eta$は、理想ケースでは1、SLPが計算速度を向上させなければ0、また計算時間が延びれば負の値を取ります。表2はプールで並列実行される次の3つのセクションの実行時間を、プールサイズ1,2,4に関して示します:一粒子軌道(OPO)と、Jastrow因子およびEwald和、もちろん全(DMC)実行時間も示します。入力ファイルは共有メモリーベンチマーク計測で用いたものと同じです(表1を参照してください)。効率パラメーターによれば、OPO計算では、プールサイズ2の時が最高の効率でした。プールサイズ4の場合はOPOはクアッドコアプロセッサーでさらに効率が良いですが、他の量は同じような性能で多少良好です。系が大きくなればOPO計算効率も向上します。
| DC | QC | |||||
| プールサイズ | 1 | 2 | 4 | 1 | 2 | 4 |
| System 1 | 1024電子 | |||||
| OPO | 118 | 80(0.46) | 78(0.17) | 141 | 93(0.52) | 64(0.40) |
| Jastrow | 271 | 218(0.24) | 189(0.14) | 199 | 151(0.32) | 123(0.21) |
| Ewald | 79 | 59(0.34) | 34(0.44) | 122 | 90(0.36) | 52(0.45) |
| DMC | 773 | 656(0.18) | 592(0.10) | 743 | 610(0.22) | 518(0.14) |
| System 2 | 1536電子 | |||||
| OPO | 267 | 171(0.56) | 143(0.29) | 311 | 197(0.58) | 136(0.43) |
| Jastrow | 640 | 505(0.27) | 473(0.12) | 454 | 340(0.36) | 317(0.14) |
| Ewald | 183 | 137(0.34) | 81(0.42) | 276 | 207(0.33) | 121(0.43) |
| DMC | 1965 | 1709(0.15) | 1531(0.09) | 1847 | 1522(0.21) | 1358(0.12) |
スレーター行列式と関連する行列計算がプールヘッドで実行されることから、DMCの全体効率はさらに小さな値となっています。CASINOではスレーター行列式は2通りのやり方で計算されます:i)$N_e^3$に比例するLU分解を使う、ii)補因子行列[9]の再帰関係を用いる、この場合は$N_e^2$に比例しますが数値的に不安定な方法です。ここでは、VMC計算におけるこの2つのサブルーチンに対し、Scalarpackルーチンを用いたプールコアでの並列計算で実装しました。表3の実行結果から、$N_e^3$アルゴリズムが非常に良い性能を示し、$N_e^2$アルゴリズムは性能悪化が示され、事実これは実行時間内で大きなウェイトを占めていました(CASINOの最新版では、スレーター行列式でのLU分解計算はデフォルトでは10万時間ステップに一回呼ばれます)。
| DC | |||
| プールサイズ | 1 | 2 | 4 |
| System 1 | 1024電子 | ||
| det $O(N^3)$ | 12 | 5.5(1.18) | 4.7(0.52) |
| det $O(N^2)$ | 94 | 106(-0.11) | 76(0.08) |
| System 2 | 1536電子 | ||
| det $O(N^3)$ | 39 | 18(1.17) | 10(0.90) |
| det $O(N^2)$ | 330 | 344(-0.01) | 231(0.14) |
4 OpenMPによる第2レベル並列化
以前の調査ではプロセッサーを跨って一つの配位を並列計算するのは効率が良く無く、同一プロセッサー内で分散する方が高性能でした。HECToRフェーズ2ではクアッドコアが装備され、ブレードに装備されたプロセッサーの共有メモリーや多数のコアを活用することが、HECToRサービスの次のステージとして期待されています。このハードウェア構成において、SLP実装への混成プログラミングの活用がまず考えられます。OpenMPを単一の配位計算を加速する手段として採用し、複数配位のセットには継続してMPIを利用します。
CASINOにおけるOpenMPループ並列は比較的容易に実装できます。コードは電子数のネストしたループパターンを含み、2つあるいは複数の電子座標に依存する関数の総和である様々な物理量計算を実行します。
OpenMP並列はその計算の最内側ループを対象とします。外側ループの並列化は理論的観点からより効率的な手法ですが、実際には以下の2つの理由からOpenMPで実装するには極めて困難です:
- コード内では同じ計算を繰り返さないように様々な値に対してバッファリング・アルゴリズムを採用しており、これがデータの依存性を導いています
- 最も重大なことは、利用しているコンパイラーのOpenMP仕様の現状の実装は、モジュール変数を使う手続き呼出しを取り扱うのに適しません。PGIおよびPathscaleコンパイラーはスレッドでプライベートとして用いるモジュール変数にバグがありました(この問題はバージョン8.0.6で解消しました)。GCCコンパイラーバージョン4.3.3は内部サブルーチンに並列領域を含む場合にはコンパイル時にクラッシュしました(この問題はバージョン4.4.0で解消しました)。こうした実装上のOpenMP仕様にためにコード書き換えが発生することがありますが、この種の作業は時間ばかり浪費して、他の開発者の作業へ不必要に影響が生じる可能性があります。理想的にはループレベルのOpenMP並列ではシリアルコードを変更すべきではありません。
OpenMP並列のベンチマーク測定を、セクション3のものと同等のシステムで実施しました。CASINOはこの2つのベンチマーク測定の間に重要な変更が施されたため、数値結果の直接的な比較はできませんが、式(6)の効率パラメーターを使って2つのSLPアルゴリズムの比較が出来ました。
| threads | No.MP | 1 | 2 | 4 |
| System 1 | 1024電子 | |||
| OPO | 102 | 105 | 73(0.38) | 61(0.56) |
| Jastrow | 246 | 302 | 216(0.14) | 170(0.15) |
| Ewald | 79 | 78 | 39(1.03) | 20(0.98) |
| $\bar{D}$ | 49 | 47 | 19(1.58) | 9(1.48) |
| $R_{ee}$ | 123 | 114 | 65(0.89) | 40(0.69) |
| DMC | 672 | 723 | 481(0.40) | 363(0.28) |
| System 2 | 1536電子 | |||
| OPO | 218 | 232 | 166(0.31) | 147(0.16) |
| Jastrow | 539 | 648 | 470(0.15) | 420(0.09) |
| Ewald | 176 | 176 | 90(0.96) | 46(0.94) |
| $\bar{D}$ | 178 | 180 | 126(0.41) | 124(0.15) |
| $R_{ee}$ | 265 | 249 | 143(0.85) | 84(0.72) |
| DMC | 1542 | 1654 | 1154(0.34) | 966(0.20) |
最初に表4で示された値に関して議論すべき2つの事項があります。OpenMP並列ループの効率は変化します。効率が1以上でオーバーヘッドが極めて小さいことを示しているものに、System1のEwaldと$\bar{D}$セクションが有ります。一方、Jastrow因子の並列ループのオーバーヘッドは両方の系で極めて大きく、スケール性能はさらに良くありません。さらに極端なのはSystem2の$\bar{D}$の4スレッドのケースで、実質的にスケールして無いのですが、System1ではほぼ完全にスケールしています。こうした状況の主たる要因はキャッシュメモリー効率に有り、System2の$\bar{D}$行列サイズはSystem1ni比べ5割増しになっています。
結論として、OpenMPによるSLP実装はこのベンチマークの場合は、MPIプールアルゴリズムよりも良好な性能を示しています。Jastrow因子や$\bar{D}$等の幾つかのセクターのスケール性能劣化は今後調査すべき課題です。この領域のコンパイラーが改善され、プロセッサー当たりのコア数が増加していくに伴って、電子数の最外側ループレベルで並列計算が実装されるべきです。10コア以上のノードや1万以上の大きな電子数系で最高性能を引き出すために、ネストしたループのOpenMP並列が検討されるべきです。
5 データ入力の最適化
ここで、入力サブルーチンの性能改善について概略を述べます。このルーチンは計算開始時に様々なデータセットを読み込みます。そのアルゴリズムは道具は面倒なものですが直截的な方法です。
バージョン2.4より古いCASINOはBCデータ格納のためにASCII入力ファイルを用いていました。1000電子以上の系においては、このファイルを読み込むのに30分以上掛かり、実行を許可された最大時間(12時間)のかなりの割合を占めています。入力データファイルをバイナリーに変換したところ、読み込み時間は30秒以下になりました。ここではMPI-IOも使用しています。これはセクション2で記述したMPI-2Sアルゴリズムでの、グループ内のタスク数に関わらずBCデータの格納に1つのファイルのみが必要となる場合に有用です。
その他に、5000コア以上の実行においてconfig.inファイルの読み込みに60分程度かかる問題がありました。BCデータとは対照的にこのファイルはバイナリーファイルであり、この時間の遅延は、当初のアルゴリズムでは計算開始時に全てのタスクが配位の共有を知るためにconfig.inファイルを読み込むことが原因でした。この問題は、少数のタスクがconfig.inファイルを読み込んで関係するタスクへMPI通信で配布するという、新し配位読み込みルーチンを作成することで解決されました。この入力サブルーチンにより入力時間は、40,000タスクを用いた場合でも10秒まで減少しました。
6 結論
このdCSEプロジェクトは、量子モンテカルロコードCASINOの並列性と追加機能の性能向上を達成しました。その性能が改善されたCASINOは、最新のスーパーコンピューター上でより複雑な物理系を計算可能になりました。
ここで、dCSEプロジェクトにより最新版のコードに実装された主な改善点を以下に纏めます:
- System V共有メモリーを用いてOPOデータを共有することにより、大規模スケールモデルにおいてもプロセッサーの全てのコアを用いた実行が可能になりました。量的な観点では、2~4GBのOPOデータを用いる計算は初期コードから2倍にスピードアップし、クアッドプロセッサーにおいて4GB以上のOPOデータの場合には4倍に高速化しました。
- 入力処理の最適化は30から60分という不要な待ち合わせ時間を削減し、1000タスク実行当り3000~6000AUの工数削減をしました。
- ハイブリッド第2レベル並列化により、クアッドコアプロセッサー上の1000以上の電子系において、1.8-1.6倍高速化しました。ハイブリッド並列化により大規模系(1万電子程度)の計算が可能となる見込みです。
System V共有メモリーアルゴリズムと入力処理最適化はCASINOリリース2.4(2009年7月)版へ移植されました。CASINOのマニュアルに関連する情報が記載され、ユーザーの要求に沿う実行形式の生成を容易にすべくアップデートされました。第2レベル並列処理は2010年のリリース版へ追加が計画されていますが、開発者へ要求があれば入手可能です。
この2年で達成されたCASINOの性能を図2に示しました。40,000タスクまで良好なスケール性能が示されています。

図2 : ORNLにおけるJaguar Cray XT5上のCASINOのタスク数に対する性能。点線は理論スケールを示します。データは2009年7月のものです。
更に大規模なタスク数での性能劣化から、配位の再配置アルゴリズムの改良が必要であることが示唆されます。次のプロジェクトでは別の機能拡張が計画されており、それはCASINOを分子動力学と連携させることです。これは相関サンプル法を用いた系のエネルギーに対するQMC相関計算をさらに高速化するでしょう。
参考文献
| [1] | Kenneth P. Esler et al, Journal of Physics: Conference Series 125 012057 (2008). |
| [2] | http://www.tcm.phy.cam.ac.uk/~mdt26/casino2.html |
| [3] | Richard Needs, Mike Towler, Pablo Lopéz Ríos, CASINO User's Guide (Theory of Condensed Matter Group, Cavendish Laboratory, Cambridge, UK, 2008). |
| [4] | M. D. Towler, Phys. Stat. Sol. (B) 243, No. 11, 2573 (2006). |
| [5] | D. Alfé, M. J. Gillan, Phys. Rev. B 70 161101(R) (2004). |
| [6] | The initial code for these functions was provided by David Tanquaray, Cray UK. |
| [7] | Unix man pages. |
| [8] | http://www.hector.ac.uk |
| [9] | S. Fahy, X. W. Wang and Steven G. Louie, Phys. Rev. B 42 3503 (1990). |
