Phil Ridley
Numerical Algorithms Group
October 1, 2012
概要
本プロジェクトでは、2種の異なるCFD応用を扱いますが、これらは共に、移流、外力、散逸を解くためにCompact Accurately Boundary Adjusting high-REsolution Technique(CABARET)を用います。CABARET手法は、2次の風上リープフロッグによる更新手法を用いた、低散逸かつ低分散スキームです。このアルゴリズムは、スカラー移流に時空間で1つのセルのみから成る局所的な計算ステンシルを用いるため、分散並列の高速化に適しています。
地球物理学的流体力学においてCABARETは、準地衡的な渦位の力学における、地衡的な乱流の中緯度海洋循環のモデリングで用いられます。このコードPEQUOD(Parallel Quasi-Geostrophic Model)は、多層の構造矩形領域を用いたメソスケールの渦プロセス研究に主に用いられています。航空宇宙学においては、ジェット/フラップ相互作用の乱流モデリングに適用されます(Cfoam-CABARET)。自由噴流/ジェットと翼フラップとの相互作用の音響モデルの非定常成分のモデリングは、hot jetや複雑なジオメトリーの噴流の物理と同じく極めて難しい問題です。この計算モデルには、顕にサブグリッドスケール(SGS)乱流モデルを用いない、Monotonically Integrated LES(MILES)手法が用いられます。
Cfoam-CABARETは、複雑なジオメトリーに適した非構造的領域分割を用いますが、これは大規模HPCシステムにおいてI/O性能問題を引き起こします。一方PEQUODは、構造的多次元領域分割を用いるため、このような問題は生じません。しかしながらPEQUODはCfoam-CABARETとは違って、渦位の計算に用いるグローバルな逆変換スキームが必要となります。本プロジェクトは、Cfoam-CABARETのI/O性能改善のためにMPI-IOを実装し、PEQUODの渦位のための並列Swartztrauber楕円型方程式ソルバーを最適化します。これら2つのアプリケーションは本作業により、航空宇宙学では、細密な流体構造の、聴覚可能な周波数帯における遠方の騒音への影響の研究が可能になり、海洋モデリングにおいては今後全く新たな力学的な現実性のレベルの重要な結果創出を期待され、これらは現状コードの並列化実装で達成することが出来るものです。
本プロジェクトは、2010年12月に6人月として提案され、2012年8月に完了しました。その作業は、Queen Mary University of London、材料科学・工学部のSergey Karabasov博士と、Imperial College London、数学部のPavel Berlo博士の主管の下に行われました。
目次
1 イントロダクション
1.1 アプリケーションの概要
1.2 CABARETと地球物理学的流体力学への応用
1.3 CABARETの航空宇宙学への応用の背景
1.4 プロジェクトの概要
2 HECToRフェーズ3への実装
2.1 PEQUOD
2.2 PEQUODの性能
2.3 Cfoam-CABARET
2.4 Cfoam-CABARETの性能
3 PEQUODの渦位逆変換ルーチンの最適化
3.1 実装
3.2 グローバル集団通信の性能比較
4 Cfoam-CABARETのIO性能改善
4.1 MPI-IOの実装
4.2 Cfoam-CABARETにおけるMPI-IOの利点
5 結論
6 謝辞
1 イントロダクション
1.1 アプリケーションの概要
CABARETは、計算的な航空宇宙および地球物理の問題に適した一般用途向けの移流スキームです[1]。レイノルズ数104でナビエストークス方程式を解く場合には、この方法は、マッハ数0.05-0.1まで特に追加のプレコンディショニング無しに大変良い収束性を示します。特に、流体力学的不安定性や自由噴流のモデリングにおいては、少なくとも30倍効率的に、通常の2次スキームの結果と同等な結果を出すことが可能です[2]。CABARETは、2次の風上スキームによる更新を用いた、低散逸かつ低分散スキームです。このアルゴリズムは、スカラー移流に時空間で1つのセルのみから成る局所的な計算ステンシルを用いるため、分散HPCに適しています。
本プロジェクトでは、CABARETを用いる2種のCFDアプリケーションを、HPCアーキテクチャー上の性能改善のために最適化します。一つは航空機のジェットエンジンとフラップの相互作用による騒音で、もう一つは海洋循環におけるメソスケールの渦の遷移です。
海洋循環問題が重要なのは、海が気候変動に寄与するからです。その寄与は、メソスケールの渦固有の非線形力学により誘発され、大規模に制御されています。こうした渦の影響は非-拡散的で、時に反-拡散的なものであるため、単純な方法でパラメーラー化することが極めて困難です。渦の動力学的理解の困難さは、グローバルな気候変動予測を理解する上で大きなハードルです。
この渦を解くには、スーパーコンピューターを用いた最先端の数値モデルが要求されます。コード、Parallel Quasi-Geostrophic Model(PEQUOD)は、この領域の先端的なアプリケーションで、外力と散逸を扱う多層準地衡的渦位方程式(layered quasi-geostrophic potential vorticity equation)[3-4]を解くために開発されました。PEQUODをHECToRに最適化すれば、大規模海洋循環における渦の現実的な力学とその影響について、前例のないレベルの結果を導けるでしょう。これは言い換えれば、様々な乱流の計算を可能にすることで気候研究への重要な寄与となるでしょう。その計算とは、海洋循環の物理学的な処方であり、以下の古典準地衡的な事項におけるものです:
| 1. | 風力還流(wind-driven ocean gyres)の乱流固有の大規模低周波変動 |
| 2. | 大規模循環とその変動を左右する渦/大規模流体相互作用の物理 |
| 3. | メソスケール海洋渦による物質移動 |
| 4. | 包括的なグローバル気候モデルの海洋成分における本質的な渦効果のパラメーター化 |
更に重要なのは航空機騒音問題です。2020年には、航空機の数は2倍になるため、航空機は少なくとも2倍の静粛性を求められます。過去には、ジェットエンジンサイズを大きくすることにより、民間航空機のジェットエンジン騒音は削減されました。これはそのままの推力で速度の減少を招きます。ジェット騒F音がジェットの出口速度に比例することから、騒音も減ることになります。しかしながら更なる静粛化には、詳細な騒音メカニズムの定量化が必要で、ジェット騒音の削減は手ごわい問題です。
ジェット騒音問題に加え、機体/エンジン相互作用による機体騒音が、着陸時の航空機騒音の主要な寄与であり、その削減も問題となっています[5-6]。特に、着陸時に大きな迎え角が配置された時、フラップは大きな騒音源となります。さらに、翼下エンジン配置においては、離陸時のジェット-フラップ相互作用(JFI)が重要な騒音成分となります。
飛行条件によりこうした効果は相互に影響し合うため、そこでは高解像計算モデリングがより重要になります。非定常流の複雑性は、モデリングをしようとする計算問題の最小サイズを極めて大きくしてしまいます。しかしl高解像Cfoam-CABARETコードを用いれば、これをHECToR上の大規模モデリングへ拡張でき、騒音に寄与するジェット-フラップ相互作用の重要な非定常的効果を捕捉することが可能です。Cfoam-CABARETは、ナビエストークス方程式の解法にMonotonically Integrated LES(MILES)手法を用いています。解の非振動的性質を捉えるために、CABARETスキームは、流束変数の最大値原理に基づいた低散逸な非線形流束補正を用います。各時間繰返し毎の計算は、保存式フェーズと特性値分解フェーズから成ります。
1.2 CABARETと地球物理学的流体力学への応用
PEQUODは、矩形領域における多層の準地衡方程式を解きます。このモデルは、流域モードとチャネルモードの2種の主演算モードを持ちます。流域モードは通常、上層風駆動による系へのエネルギー導入を用いた、簡単な風力二重還流モデルとして用いられます。 チャネルモードは、横浮力駆動による系へのエネルギー導入を用いた、簡単な傾圧偏西風ジェット気流形成(baroclinic zonal jet formation)モデルに用いられます。
準地衡的渦位方程式(quasi-geostrophic potential vorticity equation)(1)は、外力と散逸に関する式で、
\begin{eqnarray} \nabla_t+J(\psi,q)=F, \tag{1} \end{eqnarray}
ここで、qは準地衡的渦位(quasi-geostrophic potential vorticity、以下では渦位と参照します)です。方程式(1)の左辺は物質微分であり、Fは外力と散逸を表します。式(1)はこの時、垂直方向の多層形式で表現され、独立なヘルムホルツ方程式の系列となります。
PEQUODにおいては、多層準地衡的渦位方程式の解法に2つの有限差分法を選べますが、本作業はCABARET手法に焦点を当てます。渦位の移流に関するこの手法は、予測子、外挿子、修正子の3ステップから成ります。予測子と外挿子ステップは、空間的な中心差分を用いて実行されます。外挿子ステップは、非Total Variation Diminishing(TVD)流束制限を用いた移流項に風上差分を用います。この手法は流束について(少なくとも)2次の精度です。
流線関数$\psi$計算のためのqに対する渦位逆変換(Potential vorticity inversion)は、線形な楕円型方程式を直接法ソルバーで逆変換することで実行されます。離散サイン変換[7]を子午線方向に実行し、その結果、東西方向のスパースな1次元ヘルムホルツ方程式が得られ、ガウスの消去法等を用いて解いています。この逆変換は、その1次元問題の解を逆離散サイン変換して完了します。
1.3 CABARETの航空宇宙学への応用の背景
現状のEPSRCのフラップ騒音プロジェクトではCfoam-CABARETが用いられています。これを用いて高解像度の音響に関するMILES計算を実施し、ジェット-翼-フラップ相互作用の予測の理解に役立てています。
Cfoam-CABARETでは、ナビエストークス方程式に対して、CABARETの各時間ステップは保存形フェーズと特性値分解フェーズから成ります。このアルゴリズムは、最初に保存形予測子ステップを実行し、次に粘性項の計算を行い、続いて外挿子ステップでロ-カルなセルベースの特性値分解が実行されます。最後に保存形修正子ステップが実行されます。
1.4 プロジェクトの概要
本ソフトウェア開発プロジェクトは2つの目標があります:非構造Cfoam-CABARETのIO性能の改善と、構造PEQUODコードのスケーラビリティー改善です。ここで、非構造と構造と言う用語は、モデルの空間分割に関する言葉として使います。
Cfoam-CABARETとPEQUODの機能の主な違いは、PEQUODが非圧縮性流体を用いるため、圧力に関する並列楕円型PDE(ヘルムホルツ)ソルバーが追加で必要なことです。PEQUODのデータ分割は、Cfoam-CABARETのものに比べて本質的により簡単です。隣接セルやパーティション間の関係は、後者の方がより複雑です。その結果、非構造グリッドへのデータの関連付けは、物理的に近い場所のデータを基に新しいデータを決定するように制御/更新することから、大きな負担となります。
本プロジェクトの当初の目標は以下の項目でした:
WP1: Cfoam-CABARETのIOの並列化
Cfoam-CABARETのIOを改善する。元のやり方では1プロセスでI/Oを行っており、マスタープロセスが非構造グリッドを読み込み、その後他の全てのプロセスへブロードキャストしていた。同様のやり方が出力に対しても用いられており、チェックポイントファイルとTechplot360バイナリーファイルは、マスタープロセスへ収集された後に書き出される。ここで、その時間間隔はユーザー指定である。MPI-IOモデルを実装すれば、5×107セルグリッドは、通常のシミュレーションにおいて少なくとも1000コアを用いて5分以内に読み込むことが可能になる。
WP2: 準地衡方程式用のCABARETの並列化
スケーラブルな多層準地衡方程式ソルバーを開発し、二重還流の準地衡モデルのベンチマークを行う。このモデルは3層から成り、1025×1025の一様なグリッド上の外力と散逸過程と、風外力パラメーター化、および横粘性/底面摩擦パラメーターを含む。これは以下のステップで行う:
WP2.1: 計算グリッドに対する構造化空間分割の実装
全領域は分割され、各プロセスがその各サブセクションに割当てられる。
WP2.2: 並列構造CABARETの実装(非圧縮性流体向け)
準地衡方程式並列ソルバーを開発する。これは、セル中心の保存形変数をセル変数へ補間する保存形予測子ステップと、保存形変数と流束変数の更新のための局所的な特性値分割が行われる外挿子ステップに対する、非同期MPIの実装である。このコードを、結果が良く知られた中心リープフロッグ差分と中央差分スキームの古典的な並列実装に対して検証する。
WP3: ヘルムホルツ・ソルバーの並列化
スケーラブルな多層準地衡方程式の開発。これには標準的な楕円型方程式ソルバーが含まれ、閉じた領域か帯状の周期チャネルにおいて、渦位を逆変換して速度流線関数を計算する。この方法は、フーリエ解析と方向毎のサイクリック・リダクション法を用いる。コードを二重循環準地衡モデルでベンチマークする。
WP2とWP3の目的は、グリッドの地平間隔1kmを用いたモデリングを可能にし、CABARETの移流スキームで6km以上の乱流スケールが十分正確に表現できるようにすることです。歴史的に、1kmの解像度を持つ風力海洋循環モデルの長期変動計算に用いる鉛直方向の精度は、貧弱なものでした。比較的高次の垂直モードとその大規模な振る舞いの非線形相互作用の研究も、10層を用いて可能になります。最終的に、2km,4km,8kmグリッド間隔での実行も可能になります。WP1の目的は、典型的なシミュレーションにおいてIO時間を5倍短縮することです。
2 HECToRフェーズ3への実装
2.1 PEQUOD
PEQUOD(the Parallel Quasi-Geostrophic Model)は、矩形領域の多層準地衡方程式を有限差分法で解くコードで、主にメソスケールの渦プロセスの研究に用いられています。PEQUODは、MPIを用いて分散メモリーマシン向けに並列化されており、Fortran90/95言語の先進機能(例えば、派生型データ、ポインター、動的メモリーアロケーション、再帰型サブルーチン、関数オーバーローディング等)を活用しています。行数は約1万行です。構造カルテシアングリッドモデルを用い、各層に1次元あるいは2次元分割が可能です。これは、各プロセスを1つのパーティションに割当てる完全な構造分割を用います。
CABARETの準地衡方程式解法は、完全に陽的に解くものですが(逆行列計算は不要)、パーティション境界において、適切なプロセスからの通信を必要とします。これは、ハロ(haloあるいはghost)ノードを用いた、隣接パーティションとのノンブロッキングMPI ISENDおよびMPI IRECVによる通信です。MPIに関するカルテシアン・トポロジーも隣接パーティション決めに用います。コードのこの部分については、完全な有限要素法と最近接セルを用いたアルゴリズムが使用されることから、スケーラビリティーは線形なので、以降での議論の対象にはしません。
準地衡方程式の解法は完全に陽的ですが、渦位逆変換(potential vorticity inversion)ステップはそうではありません。これは渦位から流線関数を得るために、ヘルムホルツ問題を逆変換しなくてはならないため、陰的に解く必要があります。さらに、ヘルムホルツ演算子が楕円型であることから、本質的に非局所的な手続きです(直説法ソルバーにおいて情報の通信が必要です)。
このステップは、1次元並列ヘルムホルツ・ソルバーをデータ変換と共に用います。系は(通信を介して)再分割され、新しいパーティションは子午線方向に連続になります(第一データ変換)。これにより、各プロセス上でローカルな子午線方向の離散サイン変換を実行可能にします。この時、1次元ヘルムホルツ問題は、Schumann-Strietzelアルゴリズムを用いて並列に逆変換されます。次に逆離散サイン変換をローカルに実行します。最後に、元のパーティションとなるように再分割されます(第二変換)。グローバル通信が必要となるため、派生型データを用意し、データ変換をMPI_ALLTOALLWを用いて実装しました。
2.2 PEQUODの性能
HECToRフェーズ3での性能を図1に示しました。ベンチマークテストケースはWP2で述べたもので、二重還流の準地衡モデルです。1025×1025の均一グリッドで3層を用いました。全実行において飽和したノードを用い、デフォルトのコンパイラーによる性能を比較しました。個別のコンパイラー最適化オプションは、GCC -O3 -ffast-math; PGI -fast -O3, CCE -O3です。
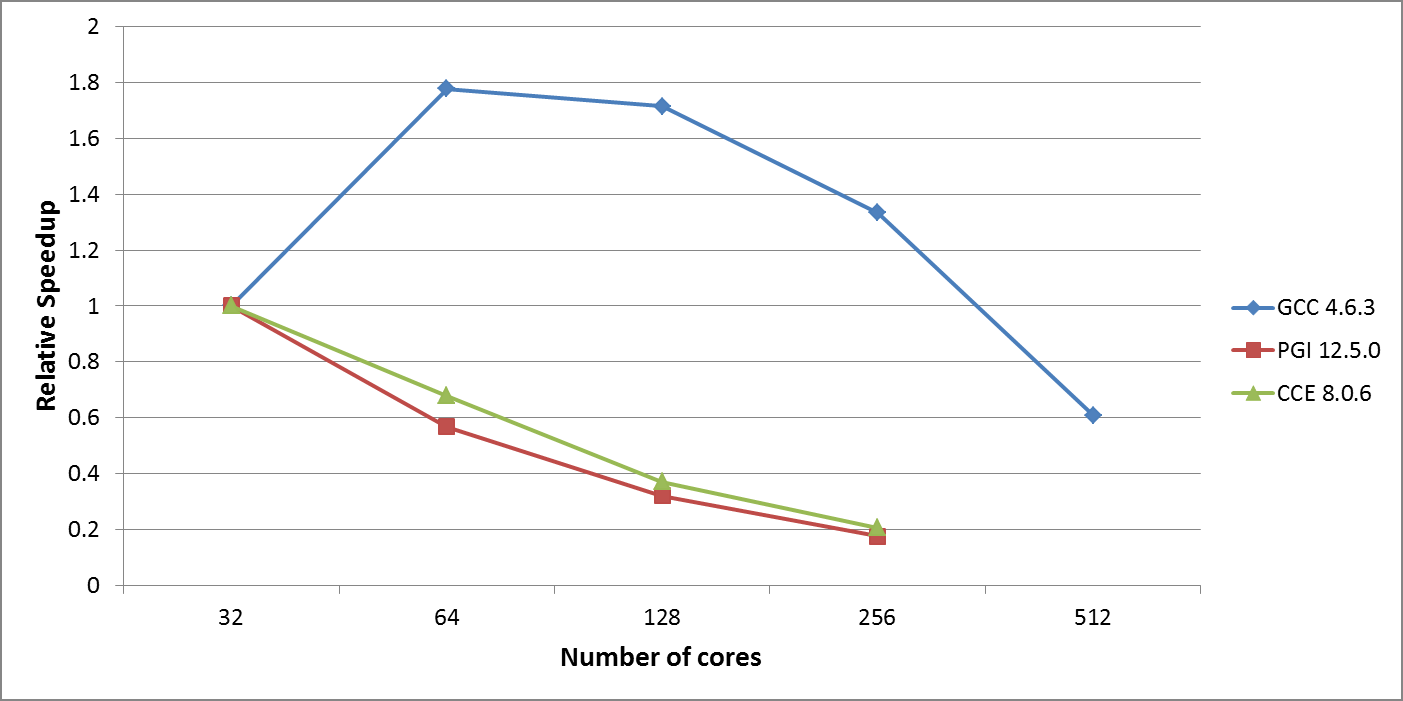
図1:HECToRフェーズ3における初期のPEQUODのスケーラビリティー
GCCが最高性能でした。最も時間の掛かる部分はCABARETの外挿子ステップですが、この部分は線形にスケールし、通信も僅かなので、全体に占めるコストはそれほど大きくありませんでした。2番目にコスト高のルーチンは、逆離散サイン変換ステップで、これは渦位逆変換ステップでの流線関数計算時に時間ステップ毎に実行されます。しかしこの計算は、データ変換のグローバル通信が要因でスケールせず、コード性能面の問題となります。GCCがPGIやCCEよりも良い性能を出すのは、逆離散サイン変換ステップがGCCに最適化されているためです。
しかしながら、GCC版PEQUODでさえ、HECToR上でのスケーラビリティーには大きな制約があります。この重大な懸念から、将来的なコード利用にはその最適化が必要です。WP2の準地衡CABARETコードの並列化は、CABARETが持つ構造グリッド性から直截的な作業です。一方WP3のヘルムホルツ・ソルバーの並列化は、それほど単純な作業ではありません。
2.3 Cfoam-CABARET
最初のCABARETに対するdCSEプロジェクトにおいて、OpenMP/MPIハイブリッド並列バージョンが実装され、5×107セル以上の問題に対して、HECToRの1000コア以上でスケールしました[8]。このコードはGambit(Fluent)が生成した非構造グリッドを用い、領域分割の前処理が必要です。また、チェックポイントと可視化用にデータを各プロセスから収集したり、最初のGambit(Fluent)が生成した非構造有限要素メッシュをブロードキャストするために、一つのマスタープロセスを利用しています。Gambitの非構造メッシュに対して任意のデータ分割が可能ですが、幾何学的配置が可能な構造的分割が推奨されます。
2.4 Cfoam-CABARETの性能
非構造CABARETのスケーラビリティー検証のために、レイノルズ数5000、マッハ数0.1で、境界条件を層流にした3D後方ステップジオメトリーを用いました。グリッドは5.12×107の6面体セルを用いて、IOを除外した276時間ステップを測定しました。HECToRフェーズ2b(Cray XT6, 24コアのメニーコア・プロセッサー)上で、100コアまで80%の並列効率が実証されました(PGI 10.8.0)。この計算には、ノード当たり4MPIプロセスで各6OpenMPスレッド、および2MPIプロセスで各12OpenMPスレッドを用いました。
しかしながら、Gambitが生成した5×107セルに対して、入力時間は約18分掛かり、Techplot360データファイル出力には25分以上掛かりました。入力ファイルはASCIIファイルですが、チェックポイントファイルはバイナリーデータなので、出力は高速で通常は10分掛かります。しかし全ての実行時間は1000コア以上では線形に増加します。よってこのプロジェクトではIO性能を改善します。
本プロジェクトの初期段階で、非構造CABARETはCfoam-CABARETへ発展しました。主な違いは、初期入力グリッドの生成にGambitを用いなくなったことと、その代わりに非構造グリッド生成とその並列分割にOpenFOAM 1.7.1を用いる事です。入力ファイルの読み込み時間は改善され、Gambit生成メッシュの1プロセス手順に比べ半分になり、出力時間も改善しました。しかし、これは入出力ファイルを分割したことによる要因でしかありません。これは、OpenFOAMのIO機能で、この他にoutFoamXと呼ばれるプリポスト処理アプリケーションがあり、分割された出力ファイルを収集しTechplot360のための単一ファイルを生成するために開発されたものです。
Cfoam-CABARETでは入力グリッドは、各プロセスに対応する部分がプロセッサー*のディレクトリー(記号*はMPIプロセス数を表すこととします)に保持されているように保存されます。各ファイルは、シミュレーション初期に各プロセスにより読み込まれます。リスタートと可視化用には、プロセッサー*のディレクトリーにResCells000000nおよびResFaces000000n(nは時間ステップ)として書き込まれます。リスタート時には、ResCells000000nおよびResFaces000000nは各プロセスについて該当する時間ステップから読み込まれます。ポスト処理ではoutFoamXは、OpenFOAMグリッドと共にResCells000000nおよびResFaces000000nを読み込みます。outFoamXの出力は、Techplot360による読み込みに適した形の一連の*.pltファイルです。
この方法は、一つのマスターIOプロセスを用いるよりも高速ですが、ポスト処理が必要なファイル数が極端に増えた場合はHECToRファイルシステムで問題が生じます。例えば典型的なシミュレーションでは、各MPIプロセスに対して1000ファイルが要求されます。つまりMPI-IOモデルの実装は、Cfoam-CABARETが要求するファイル数を減らすのに依然として適切であり、異なるプロセッサー数に対してもリスタート/ポスト処理を可能にし、必要があればOpenFOAM入力グリッドに対しても可能です。この開発についてはセクション4でより詳細に記述します。
3 PEQUODの渦位逆変換ルーチンの最適化
CrayPATによるPEQUODの詳細プロファイルは、ヘルムホルツ・ソルバーの渦位逆変換ルーチンが非効率な通信を持ち、問題サイズに対するスケーラビリティーに制約を課しています。
3.1 実装
ヘルムホルツ方程式の1D三重対角並列ソルバーは、初期の実装ではMPI_ALLTOALLWを5回呼び出し、時間ステップ毎に3層各々に対して実行されます。しかしながらこのコードにおいては、呼び出し回数よりも各呼び出しに掛かる時間が重要です。集団通信に関して最初に気づくことは、MPI_ALLTOALLWで用いるデータ型の配列内の要素が同じであることです。よって、MPI_ALLTOALLWとMPI_ALLTOALLVの違いがデータ型の違いを許すことのみのため、MPI_ALLTOALLWをMPI_ALLTOALLVへ以下のように置き換えました:
call mpi_alltoallw(psi(1, 2), ge_c%scounts1, ge_c%sindices, ge_c%types, & & ge_c%recv(1, 1, 1), ge_c%rcounts1, ge_c%rindices, ge_c%types, & & decomp_j%cart_comm, ierr); call mpi_alltoallv(psi(1, 2), ge_c%scounts1, ge_c%sindices/8, & MPI_DOUBLE_PRECISION, ge_c%recv(1, 1, 1), ge_c%rcounts1, & ge_c%rindices/8, MPI_DOUBLE_PRECISION, decomp_j%cart_comm, ierr);
MPI_ALLTOALLVはMPI_ALLTOALLWよりも効率的であることを期待しましたが、実際には5-10%悪化しました。
次に、MPI_ALLTOALLとバッファーを用いた手法を実装しました。これは、コード内で利用可能な情報を用いています。この手法の利点は、ハードウェアに最適化された集団通信(Geminiインターコネクト)を生かすことが出来ることですが、MPI_ALLTOALLが固定長のバッファサイズを要求するという欠点があります。こうしたことを考慮して、バッファが効率的にパッキング/アンパッキング可能なコードの開発が必要です。最初に、バッファサイズを各プロセスでのパッキングデータの最大サイズの2倍にセットすることで、ゼロを含む最大サイズ以下に全てのバッファを対応させます。この目的は、各プロセス上の全てのバッファ同等に、同じデータ型(MPI_DOUBLE_PRECISION)にして、以下のような呼出しを可能にすることです:
call mpi_alltoall(c_full,2*max_ii2s,MPI_DOUBLE_PRECISION, & & coeff_full,2*max_ii2s,MPI_DOUBLE_PRECISION,decomp_j%cart_comm, ierr)
この呼出しの前に、送信バッファ(c_full)はパッキングされており、呼出し後には受信バッファ(coeff_full)はアンパッキングされなければなりません。これは、配列psiからc_fullへのコピーと、coeff_fullからge_c%recvへのコピー操作を含むループの中に実装されます。このループは、ge_c%scounts1とge_c%rcounts1のストライドを持つメモリーアクセスも組み込まれ、これは不可避でしたが、幸運にも性能上の問題は生じませんでした。
3.2 グローバル集団通信の性能比較
新しいMPI_ALLTOALL実装のスケーラビリティーを図2に示します。WP2のベンチマークテストケースの強スケール性能は、HECToRフェーズ3の256コアまで良好になりました。これは当初64コアまでの利用に制限されていたものです。PGIの性能が良くありませんが、スケーラビリティーは改善しました。CCEはスケーラビリティー改善を示さず、図1のMPI_ALLTOALLWと似た結果です。
新旧の実装の正確な比較を図3に示します。明らかに、性能の傾向は両方の実装で似ていますが、通信コストは新しいグローバル集団通信で劇的に減少しています。
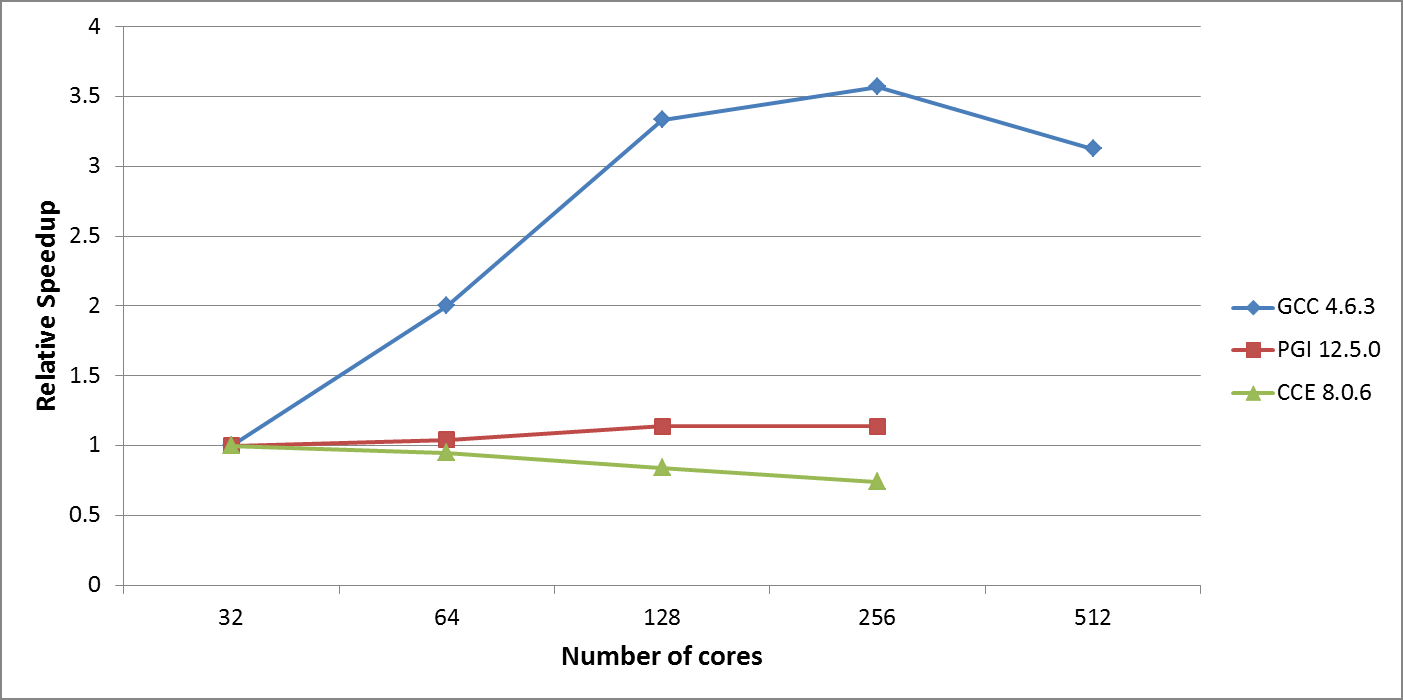
図2:HECToRフェーズ3における改善されたグローバル集団通信を用いたPEQUODのスケーラビリティー
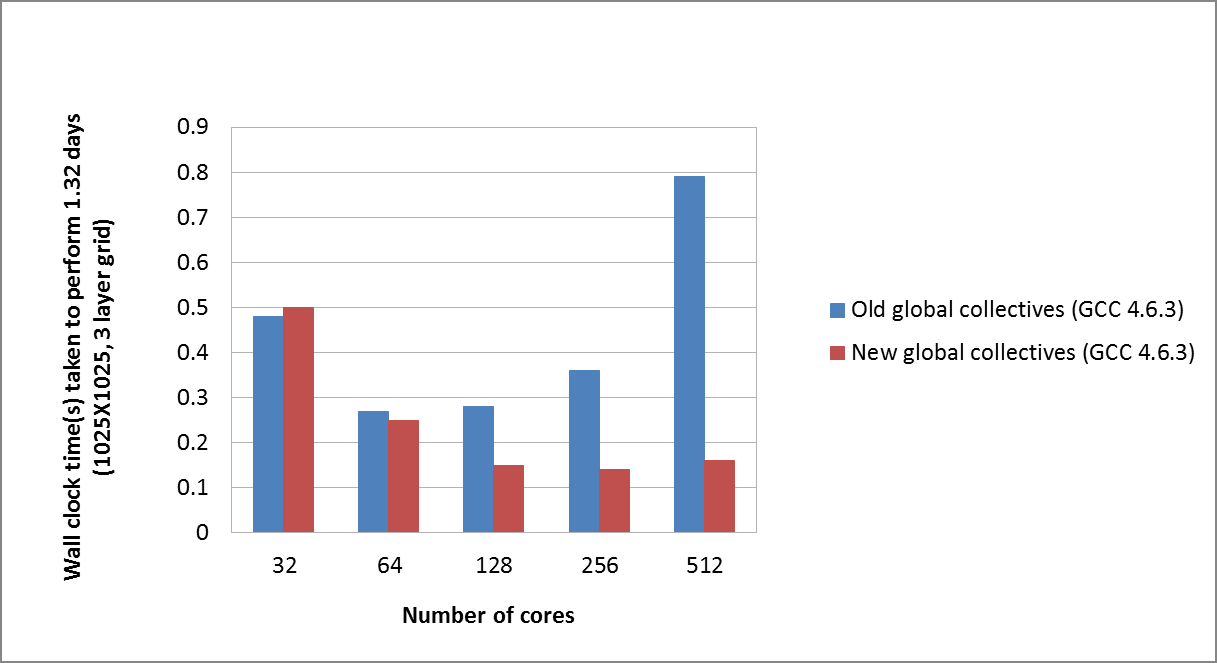
図3: PEQUODの新/旧グローバル集団通信の比較
新しい実装の弱スケーリング性能は、16385グリッド問題サイズ(これは試験した最大サイズです)まで良好なことを検証しました。この結果は図4に示されています。全ての実行はGCC 4.6.3を用いました。
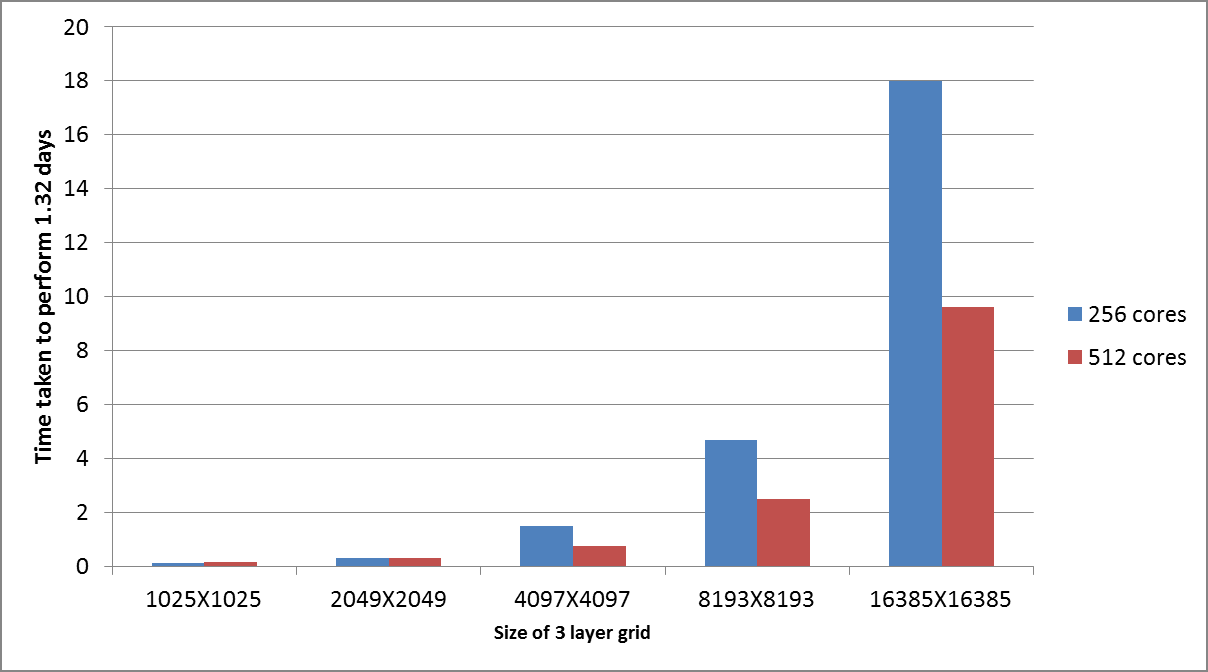
図4: PEQUODの新グローバル集団通信を用いた弱スケーリング性能
4 Cfoam-CABARETのIO性能改善
このセクションではCfoam-CABARETへのMPI-IO導入の開発を纏めます。これは、リスタートと可視化データファイルを生成するコードの一部となります。OpenFOAMから生成された入力グリッドは、変更はありません。出力ファイルは、プロセッサー*のディレクトリー(*はMPIプロセス数)にResCells000000nおよびResFaces000000n(nは時間ステップ)として書き込まれます。本作業の目的は、各プロセッサーに対する複数ファイルの代わりに、ResCells000000nおよびResFaces000000nという単一のファイルへの書き込みをMPI-IO実装することです。
更に、これらのデータはポスト処理アプリケーションoutFoamXでも利用が可能で、これはTechplot360で読み込む際に適した一連の*.pltファイルを生成します。よってCfoam-CABARETとoutFoamXの両方が、MPI-IOを用いる際に必要です。目的は必要なファイル総数の削減です。
4.1 MPI-IOの実装
Cfoam-CABARET内の、リスタートファイルと可視化データファイルであるResCells000000nおよびResFaces000000nの出力を行うサブルーチンWriteResを更新して、MPI-IOを用いて個々のセルデータやセル面データを一つのファイルへ書き込むようにします。新しいデータファイルからリスタート可能にするには、サブルーチンReadRestartFileも同じファイル構造でMPI-IO化しなくてはいけません。これは、直截的には、コード内のデータオフセット定義情報と併せた、MPI_FILE_READとMPI_FILE_WRITEによる実装です。
outFoamXへMPI-IOを実装する際には、主にTechplot360に必要なポスト処理に関する作業が必要です。当初のoutFoamXは、最初に別々のファイル:ResCells000000nとResFaces000000nを各プロセスで読み込み、次に内部的なポスト処理が実行され、最後にデータはマスタープロセスへ集約されて、Techplot360への入力となる単一の.pltファイルをシングルプロセスとして書出しています。
outFoamXをMPI-IOに対応させるために、サブルーチンGatherOutputFromAllProcsと、PostProcessor、およびReadCubesを修正しました。この新しいコードは、ResCells000000nとResFaces000000nを単一ファイルとして読み込み、Tecplot360用の単一.pltファイルを並列に書出します。
4.2 Cfoam-CABARETにおけるMPI-IOの利点
Cfoam-CABARETへのMPI-IOの追加は、大規模なMPIプロセス数を用いた場合に、HPCマシン上のスケーラブルなIOにとって重要になります。2.5×107セルテストケースで1000以下のMPIプロセスを用いた場合は、MPI-IOは元の手法より20%遅くなります。しかしながら、多数のポスト処理ファイルが要求された場合には、実行中に多くのファイルへアクセスすることを避けるためにはMPI-IOが必要になります。更に、1000以上のプロセスの場合は、MPI-IOは少なくとも元の手法と同等の性能を示し、数千ファイルを扱う問題を避けることが出来ます。
5 結論
本プロジェクトにおいて、2つの重要なCFDアプリケーションが更新されました:一つは海洋モデリングにおけるメソスケールの渦プロセス研究に用いられるPEQUOD(the Parallel Quasi-Geostrophic Model)、もう一つは、航空宇宙学の擬DNSシミュレーションのためのCfoam-CABARETです。これらは共に、移流方程式を有限差分スキームで解くCABARET法を用います。PEQUODは、1D三重対角並列ソルバーのグローバル集団通信をハードウェアに最適化された集団通信MPI_ALLTOALLを実装することで更新されました。典型的なグリッドサイズ1025点では2倍高速化し、MPIタスク当たりのグリッド数を固定した場合には良好な弱スケール性能を示しました。Cfoam-CABARETは、リスタートファイルとTecplot360用の可視化データファイルに対してMPI-IOが導入されました。これにより、実行時に必要だった数千ファイルが不要となり、HECToRや将来のHPCアーキテクチャーでのより実際的な利用が可能になりました。
PEQUODの利用により、将来的に様々な研究に利益をもたらします。気候モデリング研究者にとっては、海洋内部の非線形ダイナミクスが如何にして気候変動に寄与するかに興味を引くこととなるでしょう。海洋観測研究者にとっては、正確な推定が要求される、大規模低周波数変動や渦場等の特性の理解が興味を引くこととなるでしょう。包括的な一般的循環モデルを用いる気候モデリング研究者は、これまで用いて来た渦を解像しないコードや部分的に渦を解くコードを強化することが可能になります。PEQUODの成果はその道筋を示すことになるでしょう。これらは、固有の大規模低周波数変動や関連する渦効果が極めて基本的な課題と捉える理論研究者にも有益でしょう。
多くの研究論文が準地衡的乱流の様々な側面を扱っていますが、乱流や動力学のより現実的な解に対する要求はますます増加しています。動力学的な現実性の全く新しいレベルを持つPEQUODとHECToRの組合せでのみ到達可能な、刷新され、更新されることを待ち望まれる、興味深く重要な仕事が存在します。これは以下の研究事業に関連します:NERC project (NE/H020837/1) "A new approach to parameterising ocean eddies: energetics, conservation and flow stability",October 2010-September 2013.
Cfoam-CABARETとジェット-フラップ騒音においては、その結果は幾つかの重要な科学的課題に答える手段を強化するでしょう。その一つが、細密なスケールの流体構造が、"聴覚可能な周波数帯における遠方の騒音へどのような影響を与えるか?"という課題です。非構造CABARETをベースにした強化された数値計算モデルとHECToRを用いて、グリッド分解能が大幅に改善されたことによりこの課題回答が可能になるでしょう。これは以下の研究事業に関連します:EPSRC projects (EP/I017747/1) "Flap Noise", April 2011-September 2013および、(EP/I017771/1) "Aerodynamics and aeroacoustics of complex geometry hot jets", November 2011- September 2015.
6 謝辞
このプロジェクトは、nAG Ltd.が運営するHECToRの分散計算科学および工学(CSE)サービスの基に実行されました。英国の国立スーパーコンピューティング・サービスである、HECToR:英国リサーチ・カウンシル・ハイエンド計算サービスは、リサーチ・カウンシルを代行するEPSRCが管理しています。そのミッションは英国学術界の科学および工学の研究支援です。HECToRスーパーコンピューターは、UoE HPCx Ltd.およびnAG Ltd.のCSEサポートサービスにより管理運営されています。
PEQUODのリード開発者である、オックスフォード大学のJames Maddison博士、および、Cfoam-CABARETのリード開発者であるケンブリッジ大学のVasily Semiletov博士に感謝します。
文献
| [1] | "Compact Accurately Boundary Adjusting high-REsolution Technique for Fluid Dynamics", S.A. Karabasov and V.M. Goloviznin, J. Comput.Phys., 228(2009), pp7426-7451. |
| [2] | "CABARET in the Ocean Gyres", S.A. Karabasov, P.S. Berloff and V.M. Goloviznin, Journal of Ocean Modelling, 30 (2009), p55168. |
| [3] | "Geophysical fluid dynamics", J. Pedlosky, Springer-Verlag, 2nd edition, 1987. |
| [4] | "Atmospheric and oceanic fluid dynamics: Fundamentals and large-scale circulation", G. K. Vallis, Cambridge University Press, 2006. |
| [5] | "Understanding Jet Noise", 'Visions of the future', S.A. Karabasov, issue of Phil. Trans. of R.Soc. A: Mathematical, Physical and Engineering Sciences, August 13, 2010, 368, pp3593-3608, doi:10.1098. |
| [6] | "Jet Noise - Acoustic Analogy informed by Large Eddy Simulation", S.A. Karabasov, M.Z. Afsar, T.P. Hynes, A.P.Dowling, W.A. McMullan, C.D. Pokora, G.J. Page, and J.J. McGuirk, AIAA Journal, 2010 (July), Volume 48, Number 7. |
| [7] | "Formulation and users' guide for Q-GCM Version 1.3.1", A. McC. Hogg, Blundell J. R., W. K. Dewar, and P. D. Killworth, 2006. http://www.q-gcm.org/downloads/q-gcmv1.3.1.pdf |
| [8] | http://www.hector.ac.uk/cse/distributedcse/reports/cabaret/(英文) https://www.nag-j.co.jp/nagconsul/performance-tuning/jisseki/dCSEreport_cabaret.htm(邦訳) |
| [9] | "Parallel solution of tridiagonal systems for the Poisson equation", U. Schumann and M. Strietzel. Journal of Scientific Computing, 10(2)(1995), pp181-190. |
