Phil Ridley
Numerical Algorithms Group
February 1, 2011
概要
CABARET (Compact Accurate Boundary Adjusting high REsolution Technique)は、圧縮性ナビエストークス方程式を解く際に利用されています。このコードは、2次の風上スキームによる更新を用いた、低散逸かつ低分散の保存形CABARET法がベースです。CABARETアルゴリズムにおいて重要な点は、スカラー移流に時空間で1つのセルのみから成る局所計算ステンシルを用いることです。
CABARETは、現在環境問題として重要な、航空機騒音の研究に用いられています。航空機騒音に重要なのは、機体/エンジン装着効果であり、この影響の削減は極めて困難な問題となっています。特に、着陸時に大きな迎え角が配置された時、下げ翼/フラップは大きな騒音源となります。翼下エンジン配置においては、噴流と相互作用するフラップが支配的な騒音成分となります。騒音予測スキームにおいて重要な要素は、高忠実度Large Eddy simulation(LES)モデルです。機体/エンジン騒音問題において、このモデルは、着目するフラップと、自由噴流、フラップ/噴流相互作用効果を正確に捉えることが必要とされます。
高解像CABARETは、粗いグリッド上の精密な流体構造を解像する能力を持つため、音響感度モデリングに必要な問題サイズを事前に下げることが出来ます。しかしながら高忠実度LESモデリングでは、計算可能なグリッド解像度に少なくとも数百万点を必要とします。そこで本プロジェクトでは、HECToRの全リソースを活用できるスケーラブルなCABARETを開発し、噴流の初期における乱流への遷移上のグリッド感度の影響や、計算においてノズル出口ジオメトリーを含めるか否かなどの流入条件の影響に関する研究を可能にします。
目次
1 イントロダクション
1.1 アプリケーションの背景
1.2 CABARETを用いる理由
1.3 プロジェクトの概要
2 HECToRへのCABARET実装
2.1 イントロダクション
2.2 コードの構造
2.3 入力グリッド
2.4 出力データ
2.5 データ並列の実装
2.6 データ分割
2.7 非構造グリッドの分割
2.8 コードの性能
3 領域分割手法の性能
3.1 パーティショナーの効率の比較
3.2 領域分割と負荷バランス
4 コンパイラーの比較
4.1 CABARETのメインループ
4.2 ループ構造
5 マルチコア・データ並列
5.1 CABARETにおける分散データ並列
5.2 CABARETのHECToRフェーズ2bへの適用
5.3 CABARETのハイブリッド並列
5.4 ハイブリッド並列CABARETコードの性能
6 CABARETのデモンストレーション
7 結論
8 謝辞
1 イントロダクション
1.1 アプリケーションの背景
一般的なCFD問題を解くための、非常に多くの高解像数値計算スキームが存在します。これらは一般には、衝撃波の捕捉か、線形波の伝播のどちらかに適したものです。一般用途の高解像スキームも存在しますが、それらの多くは複雑なステンシルと数値的ロバスト性のために、境界条件から生じる追加の実装と計算コストが必要となります。
ロバストな一般用途の高解像数値計算アルゴリズムは、乱流モデリング、特にLarge Eddy Simulations(LES)で有用です。LESは、あるしきい値以上の流れのスケール全てを解像する数値計算スキームで、このしきい値以下のスケールのものは、ユーザー選択の乱流散逸のクロージャーモデルか、数値的散逸のどちらかによる数値モデルで扱われます。後者における有効な手法の一つが、Monotonically Integrated LES(MILES)法フレームワークでの数値的な流れ補正手法の利用です。本作業では、MILES法の一つとして、Compact Accurately Boundary Adjusting High Resolution Technique(CABARET)を用います。その理由は、CABARET法が双曲型方程式の最先端の数値スキームであり、多くの対流/移流が支配する問題に、すでに成功裏に適用されている実績があるためです[1-5]。
1.2 CABARETを用いる理由
CABARETは、計算航空宇宙学や地球物理学的問題に適した、一般用途向けの移流スキームです。レイノルズ数104でナビエストークス方程式を解く場合には、この方法は、マッハ数0.05-0.1まで特に追加のプレコンディショニング無しに大変良い収束性を示します。特に、流体力学的不安定性や自由噴流のMILESモデリングにおいて、2572グリッドを用いたCABARETは、少なくとも10252グリッドが必要な通常の2次スキームの結果と同等な結果を出すことが可能です[5]。つまりここではCABARETは30倍有効です。
線形移流に対しては、CABARETは、非散逸かつ低分散な2次の風上リープフロッグ手法の修正版です。その修正は、個別の保存と時空間内のスタガード配置された流れ変数の導入から成り、このことから、時空間計算ステンシルに対して一つのセルを割り当てる極めてコンパクトな形式となっています。通常の有限差分あるいは有限体積法と比べ、CABARETには追加の独立な時間発展変数が常に存在し、支配方程式のもう一つの重要な性質である小さな位相と振幅の誤差を保持する機能を与えます。通常流束は、セル中心変数の補間によりセル面で計算されますが、CABARETでは、流束はセル中心とセル面の時間発展に明白に依存して決まります。解の振動性を抑えるために、CABARETは、流束変数の最大値原理に直接基づいた低分散の非線形流束補正を用います。
MILES CABARET法での非線形補正の重要な役割は、散逸と分散の数値的誤差間の正確なバランスを保つように、低解像スケールを解から取り除くことです。ナビエストークス方程式においては、CABARET法の各時間の繰返しは、保存フェーズと特性値分割フェーズから成ります。
1.3 プロジェクトの概要
CABARET法は、構造および非構造グリッド上で用いられます。非構造グリッド利用時に必要となる高忠実度シミュレーション用に、CABARETバージョンが開発されています。これは任意のグリッド構造を扱うことが可能で、本プロジェクトで用いるコードとなります。本プロジェクトの当初では、CABARETはシングルコアのデスクトップで主に利用されていました。
ここで、HECToRのXT/XEシステムでの利用のための、圧縮性乱流の非構造グリッドをベースにした、CABARETの分散メモリーバージョンの開発について説明します。隣接するセルとパーティションの関係は、一般に構造グリッドの場合よりも複雑です。データを非構造グリッドのレイアウトに関係づける作業は、それが物理的に近接する他の値をベースに新たな値を決めることで更新・制御しなければならないことから、大変面倒です。
本作業は以下のように計画されました:
- 並列処理のための自動領域分割を開発する。これは、CABARETの6面体グリッド構造において負荷バランスしなくてはならない。これはまた、METISやScotch利用を容易にし、メッシュジェネレータGambitからのデータ前処理ステージにより実装される。最も適した領域分割手法を調査し、少なくとも百万グリッド点でその効果を検証する。
- 内部境界(セル面と側面)間のデータ転送プロトコルを用いてCABARETのMPI並列バージョンを実装する。
- 3D後方ステップケースを用いて新しいコードの検証とテストを実施し、HECToRフェーズ2aのXT4パートの256コア使用時に70%の並列効率を実現する。
- 3D後方ステップケースを用いて、HECToRフェーズ2aのXT4パートで、新しいコードが少なくとも50百万グリッド点を用いて動作することを実証する。
本作業は、2009年3月に開始しました。MPIの実装により、HECToRノード上で最適な通信を用いてデータ分散を可能にし、100倍大きなシミュレーションが、より少ない経過時間で可能になります。
本レポートは以下の観点でCABARET開発を議論します:
- データ分割のパティション手法
- コンパイラー性能
- OpenMP/MPIハイブリッド並列の効率
2 HECToRへのCABARET実装
2.1 イントロダクション
CABARETのシリアル実行バージョンは、ロシア科学アカデミー/モスクワのGoloviznin教授グループのKarabasov博士とその協力者の、12年以上に渡る仕事の成果として作成されました。このコードは、圧縮性および非圧縮性流体に対して10万以上のグリッド点を用いて広く利用されてきましたが、最新の高忠実度MILESシミュレーションは、百万グリッド点以上が必要とされまていす。これは、分散コンピューティングに向けた再設計によるバージョンアップで可能となります。CABARETは、計算ステンシルが最近接セルの第一レイヤーからの情報のみを必要とするため、特にこの方法に適しています。
2.2 コードの構造
現状のCABARETは、約4000行のFortran90コードです。これはルーチンとして、計算グリッド入力、リスタートファイル入出力、Tecplot形式データ出力、およびメインの計算部分から成り、この計算部分は以下の5ステップに分かれます:
PHASE1:保存形予測子ステップ。隣接の保存形変数を更新します。セル変数のグリッド点への補間も行われます。
VISCOSITY:セル中心の粘性項の計算。ここではセル変数を更新します。
PHASE2:外挿ステップ。ローカルなセルベースの特性値分割を行います。ここが最も計算時間が掛かります。
BOUND:境界セルへの制約適用。ここで、流束型のセル面の値が決定されます。物理的な境界のみを処理します。
PHASE1:保存形修正子ステップ。ここでも、前回の時間ステップからセル変数値を更新します。
2.3 入力グリッド
CABARETの計算グリッドは、Gambit(Fluent)が生成した非構造線形6面体メッシュです。これはASCIIファイル内に記述され、頂点総数(NAPEX)、セル総数(NCELL)、側面総数(NSIDE)、境界条件セット総数(NBSETS)、各セルに対する側面リスト:GEMCELLSIDE、各側面のセル結合情報リスト:GEMSIDECELL、カルテシアン頂点リスト:APEX、各セルの頂点結合情報リスト:GEMCELLAPEX、各境界条件セットの側面リスト:IBOUNDから成ります。10万セルメッシュでは、このファイルは約33MBで、5.12×107セルメッシュでは約17GBになります。
2.4 出力データ
出力データは、ユーザー指定の間隔でシミュレーション中に出力されます。リスタートファイルおよびTecplot可視化ファイルの2種類が出力されます。リスタートデータは、書式なしファイルに出力され、メッシュパラメーターと現状の流束、および保存形変数値を含みます。TecplotデータファイルはASCIIファイルとして出力されます。このファイルも流束、保存形変数値、およびメッシュデータ、局所的な渦識別:Q-criterionを含みます。10万セルメッシュでは、このファイルは約15MBで、5.12×107セルメッシュでは約8GBになります。Tecplotファイルは、少なくともこのサイズの倍で、ユーザーが幾つチェックポイントを選択したかによってさらに大きくなる可能性があります。
2.5 データ並列の実装
CABARETの計算部分は要約すると、流束型のセル側面に関する変数(SIDE)をベースにした計算と、保存形セル変数(CELL)をベースにした計算から成っています。更に、隣接CELL値から計算されたグリッド点ベースの変数(APEX)も存在します。
データ並列実装では、CABARETアルゴリズムは最近接セルの情報のみを必要とするため、各プロセス上のCELL,SIDE,APEXのハロ(halo)値の保存と、計算中の適切な時点での更新が必要となります。これは、計算グリッドに関するローカルからグロバルアドレスへのマッピング情報へ追加されます。しかしながら、これは計算を通して変化しないため、このデータについては通信は不要です。
APEX配列の値は、常にハロCELLとローカルプロセスのCELL値から決定されるので、通信を必要としません。流束型SIDE値を更新する際には常に、他の隣接プロセスのハロCELL値に対する更新値の通信が必要です。これは、図1に示すように各SIDEが2つの関連するCELLを持ち、これらは必ずしも各プロセスのハロCELLとして存在するわけではないからです。
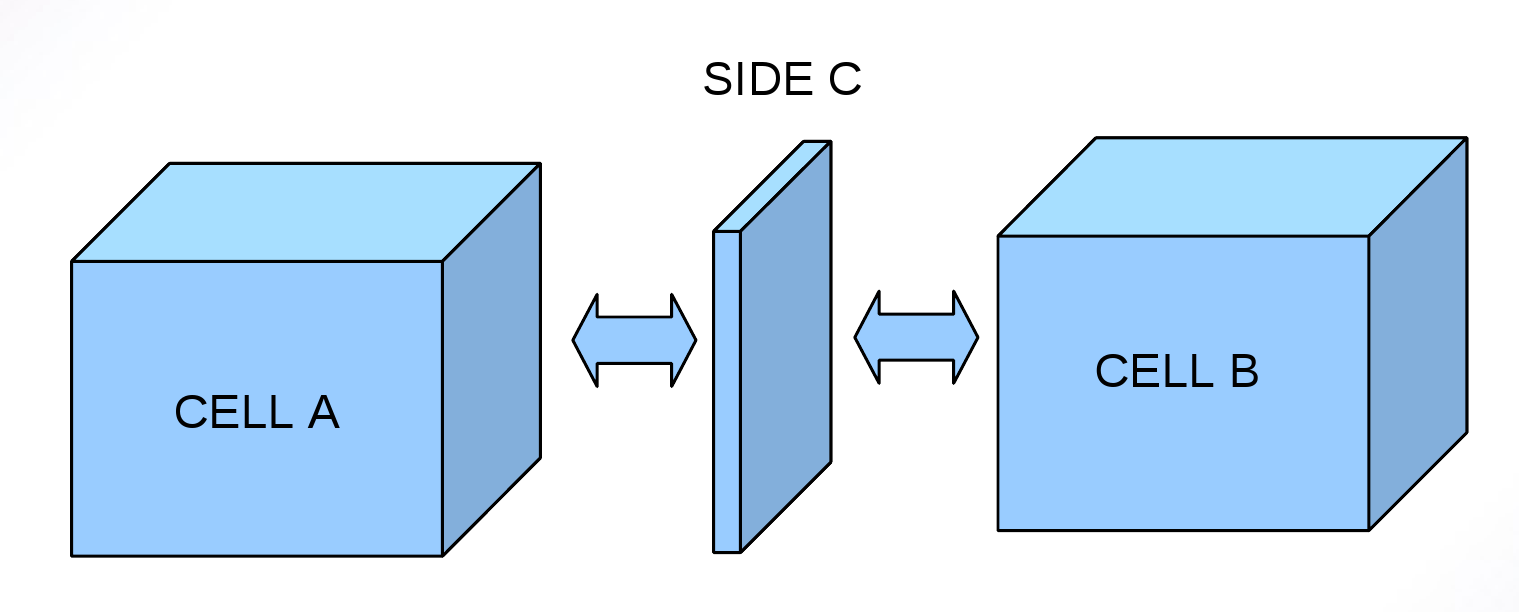
図1:2つの隣接CELLを持つSIDE
これは計算の観点からは、SIDEベースの計算のハロ値に対しては、CABARETの各時間ステップ毎に、PHASE2前と、BOUND後の両方で更新値を通信する必要がある事を意味します。実際の実装を以下に示しますが、これには、保存形および流束型(CELL,SIDE)変数両方の更新値を含む、2つの最近接ベースの通信が含まれています。
PHASE1:新しいセル(保存形)変数を計算し、これらを、隣接の保存形変数(CELL)の更新のために最近接間で通信します。またセル変数をグリッド点へ補間します。
VISCOSITY:新しいセル変数を更新します。
PHASE2:SIDEの(外挿)計算前に、流束型セル面変数をセル変数と共に隣接(SIDEとCELL)間で通信します。
BOUND:境界条件の適用。流束型セル面変数(SIDE)の新しい値を計算します。
PHASE1:セル変数を更新し、次の時間ステップサイズを決定するためにグローバルなリダクションを実行します。
各時間ステップで繰り返される計算プロセスを纏めます。これには2つの最近接間の通信と、一つのグローバルリダクションが含まれます。これは、MPIを用いてCABARETに実装され、各MPIプロセスに対してAPEX、SIDE,CELLデータにローカルな(間接的)参照システムを用い、ハロデータの更新にはノンブロッキングMPIを用いています。データ出力が必要な場合(リスタートとTecplotデータ)は、これらデータはプスト処理で2つの別のファイルへ書出すために、マスタープロセスへ送信されます。
2.6 データ分割
数値的な領域分割は、Gambit(Fluent)の非構造6面体メッシュとして作成されますが、ジオメトリーのアレンジにより、並列化に適したデータ分割が可能です。CABARETのような非構造コードは、高い並列自由度を持ちますが、そのデータアクセスは大量の間接指標を要求し、情報参照に際しメモリー操作量を増加させ、通常は局所性の劣化とデータアクセスに対する大きなレイテンシーを生じさせます。このアルゴリズムが、構造グリッドをベースにしたスキームのようにコアを増やせば効率が上がるものではないことは、言うまでも無いことです。
非構造グリッドは、結合情報リストが必要です。これは、与えられた頂点が個々のセルを形成するやり方(間接参照)を指定するものです。構造グリッドではこのリストは不要です。何故なら、ローカルからグローバルへの参照をオフセットを用いて扱うことが出来るからです。並列版CABARETの性能は、効率的なデータ分割に強く依存します。実際のデータ分割と、それが与える良好な負荷バランスと通信がシミュレーションを最適なものにします。
非構造グリッドの分割を最適化するアルゴリズムは、プロセッサーに割当てたセル数をほぼ同等にし、かつ、異なるプロセッサーへ割当てられる隣接セル数を最小にすべきです。この最初の制約は、プロセッサー間の負荷バランスを最適にすることです。後者については、隣接セルが異なるプロセッサーへ配置された場合の通信パターンを最適化を意味します。
2.7 非構造グリッドの分割
Gambitの非構造メッシュの分割には、コミュニケーターの適切なMPIプロセスへセルを割当てる必要があります。これはユーザーが用いるMPIプロセス数に依存します。その適切な方法の一つは、METIS[7,9]やScotch[8,10]のような外部の領域分割パッケージを用いる事です。その他、1,2,3次元のカルテシアン平面で横切る構造的分割という単純な方法も可能な場合があります。
外部の領域分割パッケージや構造的分割の何れを使うかは、問題とするジオメトリーに依存します。本プロジェクトのテストケース(後方ステップジオメトリー)では、一連の結果は構造的分割で十分であることを示していますが、将来CABARETで用いる任意のジオメトリーを考慮すれば、非構造的分割を扱う能力を持たせることが必要です。
コード内の通信ルーチンは、必要であれば非構造的分割手法を組み込むことが可能なように設計されました。また、別の(前処理の)分割ルーチンも開発されました。このルーチンは、外部パッケージからの分割を処理するか、構造的分割を生成するために用いられます。Gambitグリッドの非構造性から、非連続なデータが生じます。領域分割(パーティショナー)には、全グリッドを読み込める十分なメモリーを持つか、部分的に読み込むかどちらかが必要です。しかしながら、XT/XEのシングルノード上に全グリッドを読み込み、共有メモリー手法を用いる方法がより効率的です。
よってマルチコア効率を鑑みて、パーティショナーをOpenMP/MPIハイブリッド並列で実装し、最終的なコードの分割データ生成能力は、5.12×107セルのGambitメッシュに対して、250MPIパーティションで経過時間29秒以内でした(フェーズ2b(XT6:24コアOpteron 6172 2.1GHzプロセッサー。NUMAアーキテクチャーのノード当たり2つの12コアソケット)において240コアを使用し、10以上が飽和ノード。)。これは、要求されるパーティションと同数のコアを用いて実行可能です。このアルゴリズムは通信が少ないため、リニアなスケーラビリティーを示しました。
2.8 コードの性能
CABARETのMPIのみの性能を検証するために、シリアルコードに対するIOを除いた276時間ステップの経過時間を測定しました。テストケースは、3D後方ステップジオメトリー、境界条件は層流、レイノルズ数=5000、マッハ数=0.1です。グリッドサイズは10万6面体セルです。コードは共にPGI 10.8.0 Fortran90コンパイラーを用い、HECToRフェーズ2a(クアッドコア2.3GHz Opteronプロセッサー、8GB RAM)で実行しました。シリアル実行コードの時間は360秒、並列コードは50コア/13ノードで7.8秒、250コア/63ノードで2秒でした。250飽和ノードで並列効率72%です。
3 領域分割手法の性能
3.1 パーティショナーの効率の比較
CABARETでは非構造グリッドを用いるため、外部の領域分割パッケージや構造的分割の何れを使うかは、問題とするジオメトリーに依存します。可能かどうかは兎も角、カルテシアン平面による分割をベースにした構造的分割がお勧めです。ジオメトリーがより複雑な場合で、適切な構造的分割で良好な負荷分散と最適な通信を得ることは難しい時には、METIS[7,9]やScotch[8,10]のような非構造的分割アルゴリズムが必要です。並列CABARETコードは、構造的分割あるいは非構造的分割でも実行可能なように設計されました。
パーティショナーMETISはマルチレベルk-way法[12]を用い、Scotchは双対再帰的二分割(dual recursive bipartitioning)[11]を用います。性能の観点では、10万セルの後方ステップジオメトリーの分割に掛かる時間は、32,50,100,250パーティションを生成するのに、METISとScotchは同等の時間を要します。このテストではScotchが僅かに勝り、CABARET実行時間を5%削減します。しかしながら、METISは利用の容易さが僅かに勝り、ユーザーは元の非構造グリッド入力に似た入力が可能ですが、Scotchではデュアルグラフ形式が要求されます。図2は、3D後方ステップジオメトリーが非構造パーティショナーで分割される様子を示しています。

図2:単純な非構造的分割による4つの分割領域
3.2 領域分割と負荷バランス
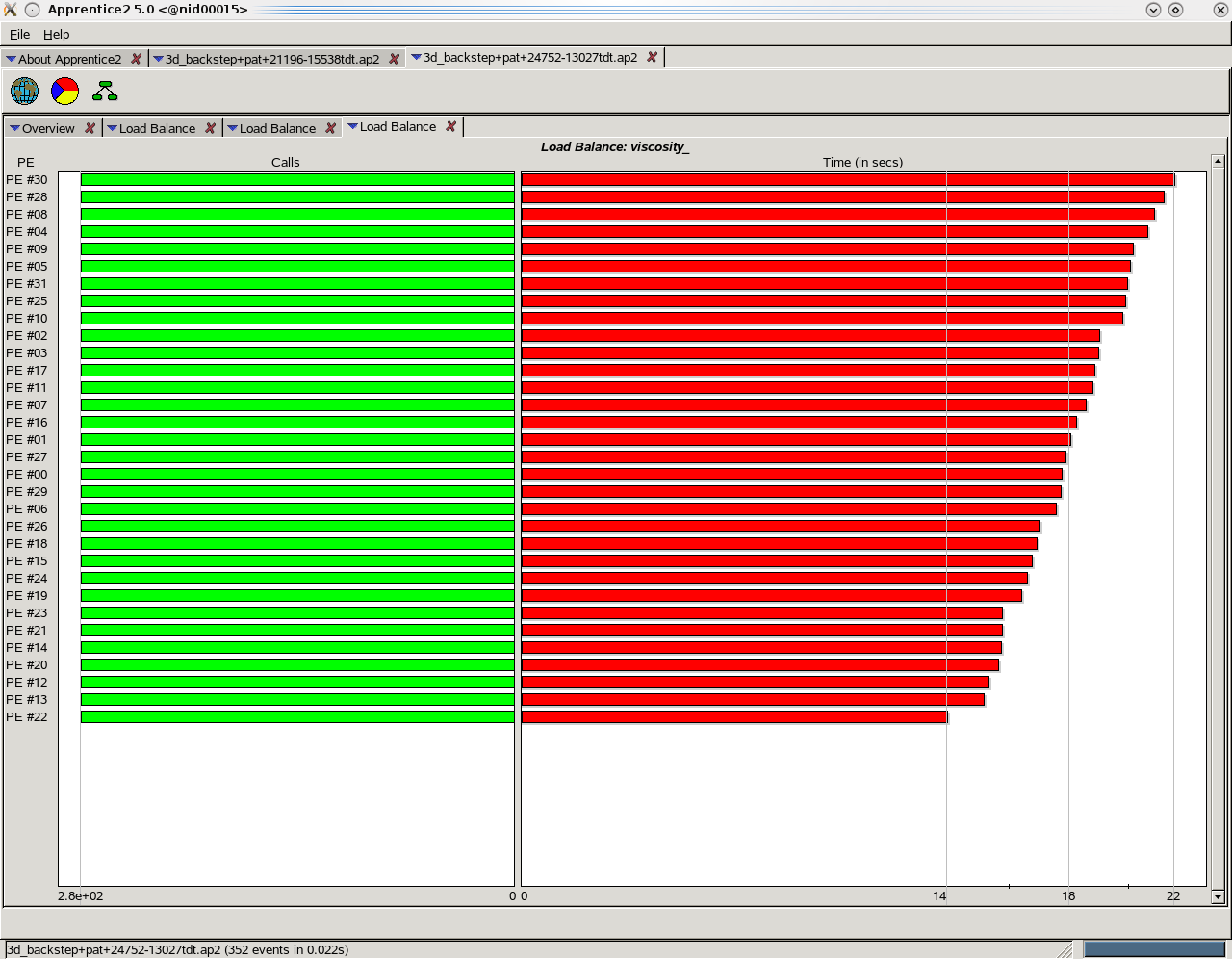
図3:VISCOSITY計算における負荷分散
Scotchによるグリッド分割がCABARETを僅かに加速する理由は、この特定の問題においては、その領域分割が負荷バランスと通信のバランスをより良い状態にするためです。図3に示すCrayPatプロファイルは、構造化されたジオメトリーに非構造的分割を適用した結果を示しています。ここには32個のMPIプロセス(パーティション)が存在しますが、プロセス番号30は、プロセス番号22に比べ3割ほど多くの時間を費やしています。これは各パーティションに対するセルの分散により生じており、境界面を含むパーティションのセル数が問題です。境界セルに依存する計算は、VISCOSITYとBOUNDで実行されます。パーティション間で境界セルの分布に分散が有る場合は、特定のパーティションで対処すべき不公平な負荷があり、これがスケーラビリティーを制限する要因となります。
3D後方ステップのような構造化されたジオメトリーにとっては、カルテシアン平面による切断をベースにした構造的分割手法がより適しています。この手法は、各MPIプロセスに均等に作業を割り振り、プロセス間通信を最小にするように用いることが出来ます。図2において1次元構造的分割を行う場合には、x軸に対して平面でパーティション分割数分に切断すればよいことが解ります。この平面分割は、境界と非境界セル両方の均等な分布を保証します(境界上のセル表面数は6面体の場合は0から6です)。CABARETアルゴリズムには有限体積法的側面があるため、隣接パーティションの決定には注意が必要です。パーティションは一つの頂点で結合され得るため、側面だけでは隣接パーティションを区別するには十分ではありません。この状況は、1次元や2次元分割では起こり得ませんが、3次元や非構造的分割では生じます。
構造及び非構造的分割を用いたMPI並列のみのCABARETの性能を検証するために、I/O無の276時間ステップの実行を用いてスケーラビリティーを測定しました。ここで用いたテストケースは、3D後方ステップ構造、境界条件は層流、レイノルズ数=5000、マッハ数=0.1、グリッドサイズは0.8×百万6面体セルです。コードはPGI 10.8.0 Fortran90コンパイラーを用い、HECToRフェーズ2a(クアッドコア2.3GHz Opteronプロセッサー、8GB RAM)で実行しました。図4は、構造データ分割を用いた場合に2倍以上高速化し、良好な負荷バランスを与えていることを示しています。
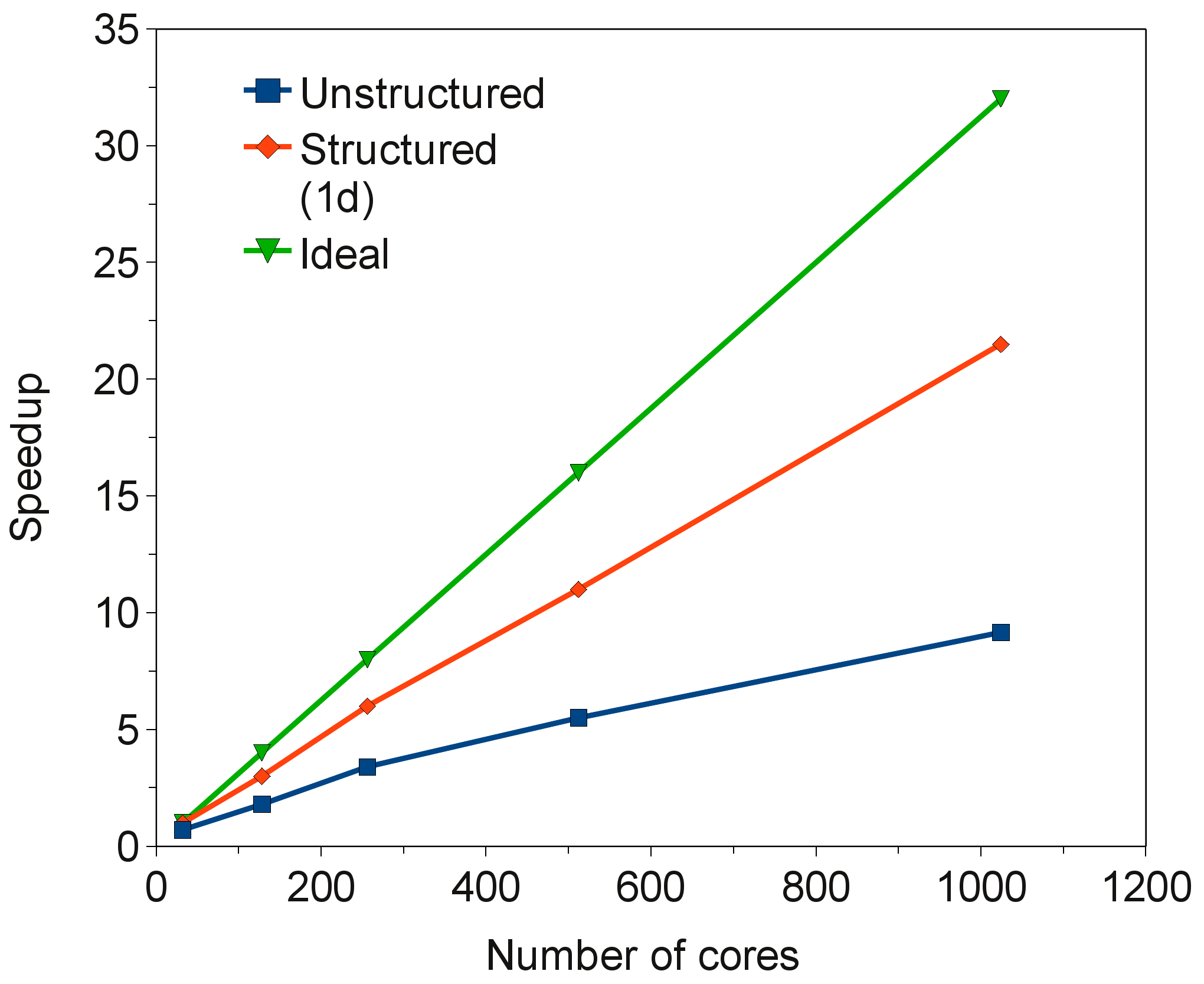
図4:VISCOSITY計算における負荷分散
4 コンパイラーの比較
4.1 CABARETのメインループ
本セクションでは、現在HECToRで用いられている4種のFortran90コンパイラー、Portland Group(PGI), Pathscale,Cray,GNUを用いた性能を評価します。CABARETの非構造グリッドとそれによる間接指標アドレス手法は、CABARETのメインループ構造へ、非連続に変化するループ構造を要請します。これらは特にベクトル化を阻害しています。
4.2 ループ構造
以下に示す2つのコード領域はベクトル化の恩恵を受けます。これらは、時間ステップ毎に呼び出される特定のサブルーチンに存在するため、CABARETの性能改善に大きく寄与します。特に、サブルーチンPHASE2, BOUND, VISCOSITYは、セル側面数のループを持っています。これらはCrayPatの解析結果において目立つ部分で、CPU時間の60%を占める最も計算負荷の高い部分です:
PHASE2, PHASE3 DO K=1,NCELL ... KEYE=KEY(K,1) NSI=GEMCELLSIDE(K,1) ... UI=SIDE(NSI,1) .... SXI=SIDE(NSI,11)*DFLOAT(KEYE) ... END DO PHASE2, BOUND, VISCOSITY DO I=1,NSIDE NCF=GEMSIDECELL(I,1) NCB=GEMSIDECELL(I,2) IF((NCF/=0).AND.(NCB/=0))THEN CALL TAKESTENCIL1F(I) CALL TAKESTENCIL1B(I) IF (ABS(CHAR3B)<DEPS) CHAR3B=0 IF (ABS(CHAR3F)<DEPS) CHAR3F=0 IF(CHAR3B+CHAR3F.LE.0)THEN... ENDIF ENDIF IF(NCF<0) THEN ... ENDIF IF(NCB<0) THEN ... ENDIF ... NCF=GEMSIDECELL(I,1) NCB=GEMSIDECELL(I,2) NSTYPE=GEMSIDECELL(I,3) NC=NCF IF(NCF==0)NC=NCB NA1=GEMCELLAPEX(NC,1) ... NA7=GEMCELLAPEX(NC,7) IF(NSTYPE==2651)THEN NSA1=NA2 NSA2=NA6 NSA3=NA5 NSA4=NA1 ENDIF ... END DO
もしコンパイラーがこれらのループに対してSSE命令を生成することが出来れば、性能改善が望めます。しかしながらこれらのループにはベクトル化対象となるものが多くなく、そのアルゴリズムはコードの再構成を困難にしています。ここで、CABARETコードをHECToRで利用可能な上記のコンパイラーバージョン、PGI 10.9.0, Pathscale 3.2.99, Cray 7.2.8 and GNU 4.5.1を用いてコンパイルしました。
結果としてどのコンパイラーも、PHASE2, BOUND, VISCOSITYに対して如何なるベクトル化も行うことはできませんでした。しかしながら、PathscaleとCrayは共に、PHASE2, PHASE3のループの部分的なベクトル化命令を生成しました。Crayコンパイラーは、必要となるベクトルレジスターの推定数をレポートします。Pathscaleコンパイラーは「LOOP WAS VECTORIZED」とレポートしました。PHASE2, PHASE3の混合数値型を止めて、DFLOATによるINTEGER KEYEのREAL(KIND=8)への型変換を消去すると、PGIコンパイラーはこのループを部分ベクトル化しました。
ここで用いた3種のコンパイラーに対する最適化オプションは、64ビットモードのターゲットプロセッサーに対して、手続き間解析、ループ・アンローリング、ループ・ネスティング(可能な場合)を用いました。HECToR上のCABARETの最高性能を持つオブジェクトを生成するという観点からは、PathscaleバージョンがPGIおよびCrayバージョンよりも平均で5%高速でした。最も低い性能はGNUバージョンで、PGIおよびCrayバージョンよりも平均で5%遅くなりました。
5 マルチコア・データ並列
5.1 CABARETの分散データ並列
本プロジェクトは、HECToRシステムのフェーズ1(ノード:dual core AMD Opteron 2.8GHz、6GB RAM)からフェーズ2a(ノード:quad core 2.3GHz Opteron、8GB RAM)への移行期に開始されました。Gambitの非構造メッシュパーティションを扱うCABARETのデータ並列は、当初MPIをベースにした上記のアーキテクチャー向けに設計されました。
このシングル・プログラム/マルチデータ手法は、Gambitが生成した計算グリッドを分割する方法を用い、分割されたグリッドに対してそれぞれCABARETのコピーで処理する手法を取っています。CABARETアルゴリズムで用いられる非構造的分割が要因となり、各時間ステップ後に必要となるハロデータへのアクセスと関連する通信において、間接参照スキームが支配します。そこで性能向上のために、非同期MPIをPHASE1, PHASE2, PHASE3に実装し、通信中に計算を実行出来るように配置しました。
本プロジェクトの半ばで、フェーズ2bのマルチコアが開発の射程に入りました。HECToRフェーズ2b(XT6:24コアOpteron 6172 2.1GHzプロセッサー。NUMAアーキテクチャーのノード当たり2つの12コアソケット)が設置され、MPI並列CABARETコードをマルチコア・アーキテクチャー対応することが必要になりました。
5.2 CABARETのHECToRフェーズ2bへの適用
HECToRフェーズ2b上でのMPI並列版CABARETの性能検証のために、I/O無の276時間ステップの実行によるスケーラビリティーの結果を図5に示します。ここで用いたテストケースは、3D後方ステップジオメトリー、境界条件は層流、レイノルズ数=5000、マッハ数=0.1、グリッドサイズは6.4×百万6面体セルです。コードはPGI 10.8.0 Fortran90コンパイラーを用いました。
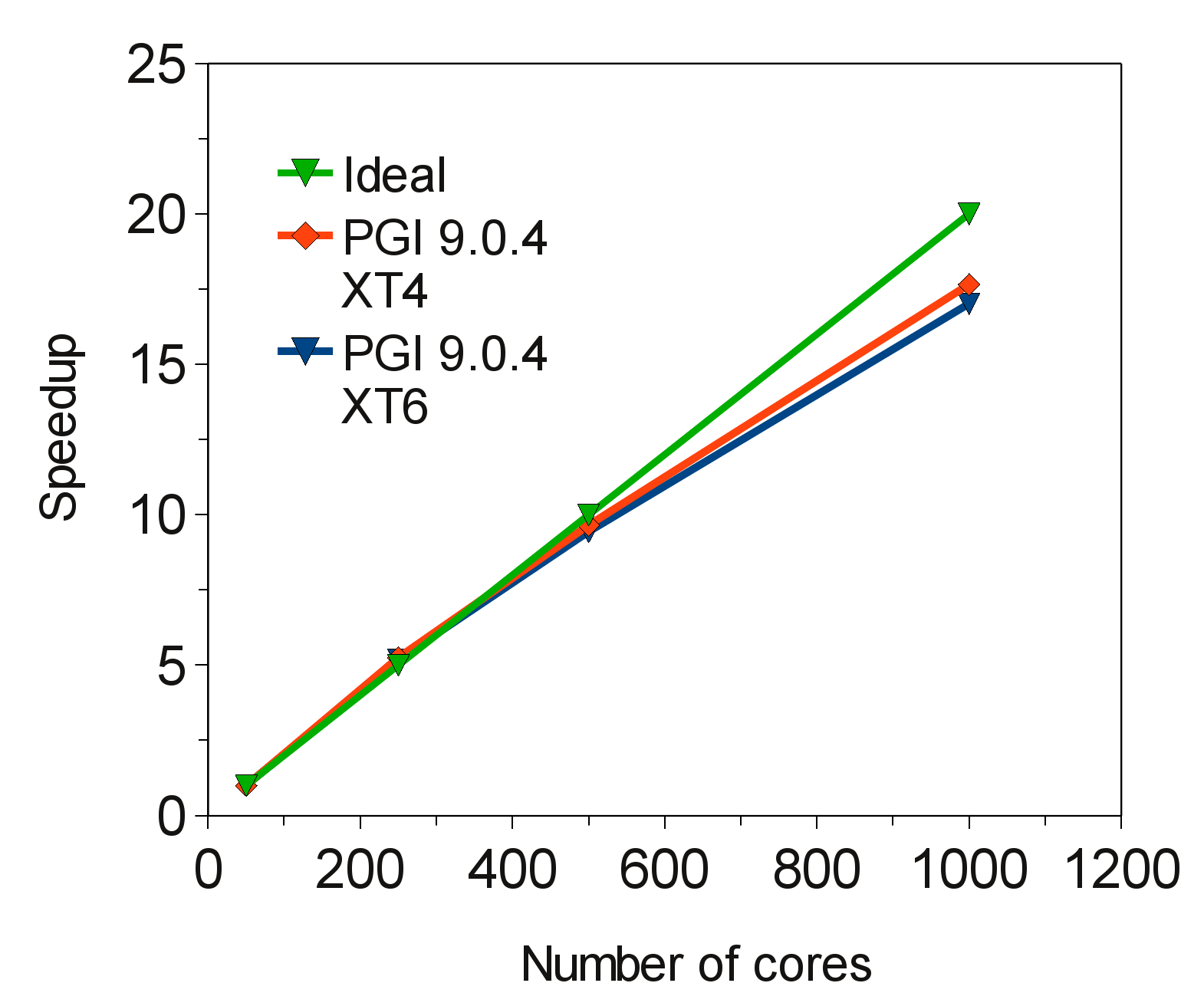
図5:後方ステップの6.4×百万セルのスケーラビリティー
図5は、フェーズ2a(クアッドコア)とフェーズ2b(Seastar2+インターコネクト)両方の結果を示しています。興味深いのは、プロセス間バンド幅の競合が増えても、クアッドコアから25コアノードへ僅かな性能劣化がある事です。フェーズ2a,2b共に、ノードはMPIタスクで飽和しています。通常、インターコネクトの競合の増加はノード当たりのMPIタスク数の増加に起因すると考えますが、この場合はそうではありません。
しかしながら、問題サイズを増やしていくと、全く異なる振る舞いを見ることができます。5.12×10百万セルの場合、図6に示したように、はっきりと影響が示されます。図5での性能は、利用可能なキャッシュとインターコネクトが収まる問題サイズだったことに起因するものです。
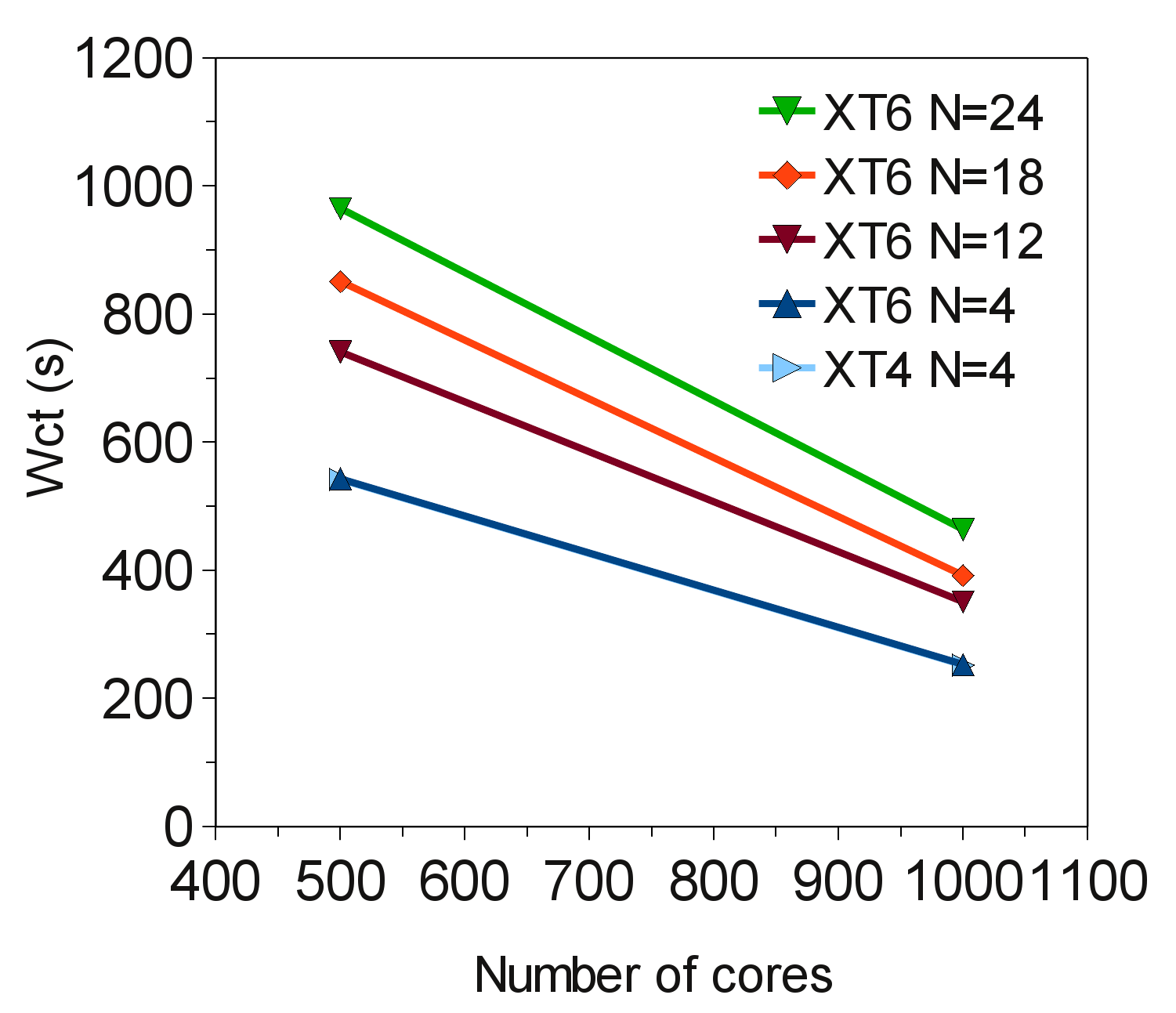
図6:後方ステップの5.12×10百万セルの実行時間
図6が示すように、500及び1000コアを用いたフェーズ2b上(XT6、Seastar2+インターコネクト)でのMPI版CABARETの実行で、経過時間は全てのケースで劣ります。ここで、ノードは、24コアを全て用いるか、ノード当たりXT4と同じMPIプロセス数(4コア)です。ノード当たり4コアのケースは、24コアのケースのほぼ半分の時間が掛かっています。こうした性能は、MPIコードをマルチコアアーキテクチャーへ移植した際の典型的な振る舞いです。
同じテストをフェーズ2bのXE6(24コア Opteron 6172 2.1GHzプロセッサー、ノード当たり2つのデュアル6core sockets、 NUMAメモリー、Geminiインターコネクト)で実行すると、ノード当たり12-24コアを用いた場合、約17%性能向上します。例えば500コアでは、Seastar2+のノード当たり24コア実行では970秒だったのが、Geminiでは805秒に減少します。
フェーズ2bのXT6とXE4の重要な違いは、インターコネクトをSeastar2+からGeminiへ置き換えたことです。Seastar2+のルーターは3Dトーラスの6リンク実装であり、ポイント・ツー・ポイント通信バンド幅は9.6GB/sです。GeminiインターコネクトはSeastar2+の1/3以下のレイテンシーで、100倍のスループットを持ち、2百万パケット/core/sの性能です。
Geminiインターコネクトは、Seastar2+に比べて高い射出レートで小さなメッセージを大量に処理することが出来ます。よって問題サイズを変化させた場合に、MPI版CABARETに対して、GeminiはSeastar2+以上の効率を示します。
5.3 CABARETのハイブリッド並列
CABARETをデータ分散手法のみで並列化する場合は、Gambitが生成した計算グリッドをサブグリッドへ分割することでデータ分散します。各サブグリッドは、グローバル・コミュニケーター内の一つのMPIプロセスに割当てられます。PHASE1, PHASE2, PHASE3においては、通信を行う間に計算を実行するように非同期MPIが実装されます。CABARETアルゴリズムで用いられる非構造的分割は、ハロデータへのアクセスと関連する通信において、間接参照スキームを用います。フェーズ2bにおいて性能を改善するためには、インターコネクトバンド幅の競合削減が必要です。そのために、共有メモリーを用いたノード内並列を用いたノード間MPI通信数の削減をします。
CABARETのハイブリッド並列実装には下記の候補があります。
| 1. | ノード上の複数パーティションにはMPIプロセスでなくOpenMPスレッドを割当てる |
| 2. | PHASE1, VISCOSITY, PHASE2, BOUND, PHASE3内の、保存形および流束変数の更新を行うループを並列化する |
これら共にノード間MPI通信数を削減しますが、1については既にCrayMPT機能に含まれており効果は大きくないため、2を選択するのが合理的で、これはCABARETに新たな並列レベルを導入します。
CABARETの計算ステンシルは、最近接グリッド点のみを必要とします。これは、計算のメインループ内にOpenMPを用いる際にとても有利です。PHASE1, VISCOSITY, PHASE2, BOUND, PHASE3内の保存形および流束変数の更新を行うループに対して、静的スケジューリングのOpenMPを指示行で実装しました。これは、サイズNCELL/OMP_num_threadsあるいはNSIDE/OMP_num_threadsを持つ部分へループを分割して、それらにスレッドを割当てます。MPI_THREAD_FUNNELLEDを用いて、マスタースレッドのみがノード間通信を実行するようにしました。
!$OMP BARRIER !$OMP MASTER DO I=1,APEXNEIGHS ! pre-post required for CELL transfers CALL MPI_IRECV(CELLD(0,1,I),10*(MAXNCELL+1) & ,MPI_DOUBLE_PRECISION,NEIGH(I),0,MPI_COMM_WORLD & ,REQUESTIN(I),IERR) END DO ! APEXNEIGHS !$OMP END MASTER !$OMP BARRIER ... !$OMP MASTER DO I=1,APEXNEIGHS CALL MPI_ISSEND(CELL(0,1),10*(MAXNCELL+1) & ,MPI_DOUBLE_PRECISION,NEIGH(I),0,MPI_COMM_WORLD & ,REQUESTOUT(I),IERR ) END DO ! APEXNEIGHS !$OMP END MASTER ... DO I=1,APEXNEIGHS CALL MPI_WAIT(REQUESTOUT(I),STATUS,IERR) END DO ! APEXNEIGHS
全てのマルチスレッドループは、最近接グリッド点のみを考慮すれば良いことから、NOWAITを用いずに実行できます。これらのルーチンがCPU時間の6割を占め、セクション4.2で議論した理由からベクトル化が不可能であるため、このOpenMP実装は効果的です。
5.4 ハイブリッド並列CABARETの性能
本セクションでは、ハイブリッド並列CABARETの性能を議論します。再び、3D後方ステップ構造、境界条件は層流、レイノルズ数=5000、マッハ数=0.1、グリッドサイズは5.12×10百万6面体セルのテストケースで検証します。テストは、MPIプロセス数(n)、ノード当たりのMPIプロセス数(N)、MPIプロセス当たりのOpenMPスレッド数(d)を変化させて行いました。また、6コアダイあるいはソケット当たりのMPIプロセスは、常に1つにしました。
図7は、276時間ステップの50,250,500,1000MPIプロセスの高速化率を示しています。比較は以下の2つの実行間で行いました:
| 1. | ノード当たり4 MPIプロセス、MPIプロセス当たり6O penMPスレッド |
| 2. | ノード当たり2 MPIプロセス、MPIプロセス当たり12 OpenMPスレッド |
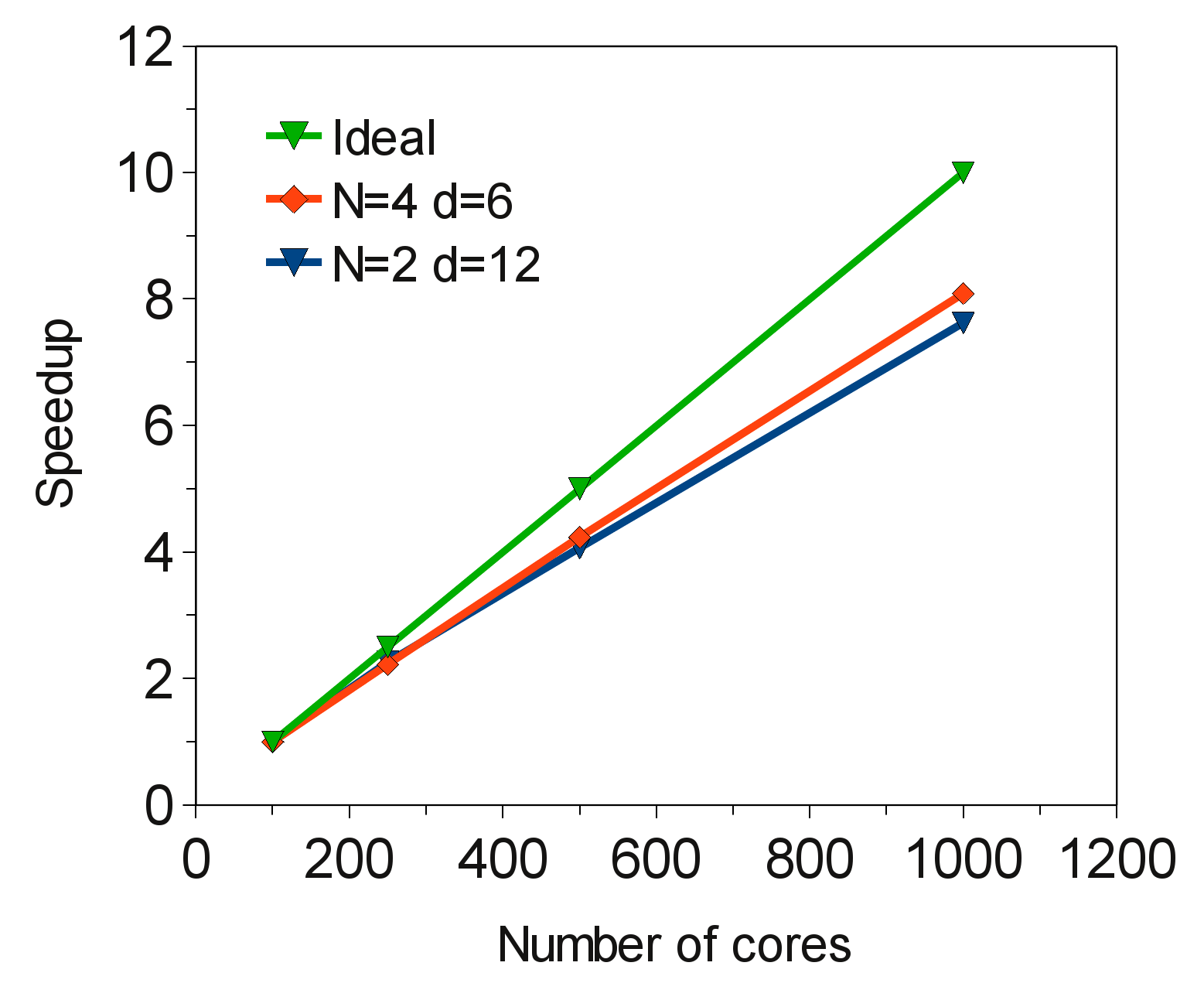
図7:後方ステップ5.12×10百万セルのスケーラビリティー
この2つの実行は、HECToRフェーズ2b/Seastar2+インターコネクト上で行いました。ケース1はケース2より僅かに優れています。これはデモンストレーションケースで、問題サイズを変えると状況は変化します。計算と通信の比率は、主要な計算ループがベクトル化されていないCABARETの性能には重要な因子です。よっていかなる問題サイズに対しても、ノード当たりのMPIプロセス数とMPIプロセス(パーティション)数に対するMPIプロセス当たりのOpenMPスレッド数の最適な数字を実験することをお勧めします。Geminiインターコネクトに対して同じテストを実施した場合は、5-10%の高速化が示されます。これは、この計算が1次元分割を用いており、それほど通信性能に依存していないことから想定内の値です。
6 CABARETのデモンストレーション
デモンストレーションとして、3D後方ステップテストケースの、40000時間ステップにおける流れ場の規格化されたx方向速度場成分を図8に示します。境界条件は層流、レイノルズ数=5000、マッハ数=0.1としました。グリッドサイズは、ステップ高に10点を用い、全体として80万点です。図9で示すように、このメッシュ解像度とステップ高に20セルを用いた場合の時間平均流れ場は、ステップ周りの正しい再循環領域長を示しました。ステップ当り20セルのグリッド密度に対する渦度(Q-norm)等値面を図10に示します。

図8:40000時間ステップにおける流れ場のx方向速度場成分
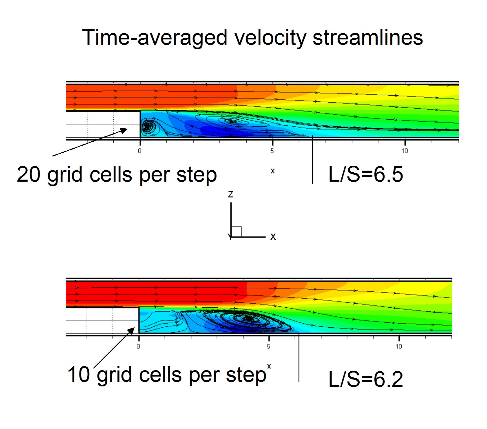
図9:2つのメッシュ解像度に対する時間平均速度場
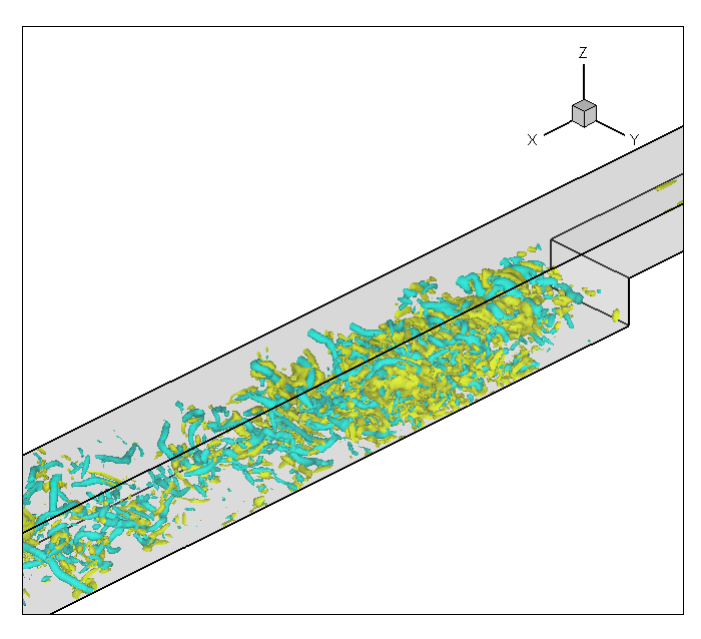
図10:ステップ当り20セルのグリッド密度に対する渦度(Q-norm)等値面
7 結論
本プロジェクトを通して、一般用途CFDアプリケーションCABARETは、英国国立スーパーコンピュータリソースHECToRへ効果的に移植され、CABARETのスケーラビリティーが実証されました。本作業は、MILESモデリングを用いて実施される先進的な研究、一般的な乱流シミュレーションを可能にし、アプリケーションの能力を一段と飛躍させました。
本レポートは、CABARETのスケーラブルなハイブリッド並列実装について報告しています。この作業はHECToRのフェーズ1からフェーズ2bの間で実施されました。CABARET手法は、高レイノルズ数、低マッハ数のLESの乱流モデリングに適しています。また、最近接セルのみを扱うため、分散コンピューティングアーキテクチャーに適しています。
入力グリッドはGambit(Fluent)が生成した非構造6面体メッシュです。これに対して自動分割手法を実装しました。これには構造的(カルテシアン平面による)分割、あるいは外部パッケージMETIS/Scotchを用いた非構造的分割のどちらかを用います。ジオメトリーのアレンジが許される場合は、負荷バランスの観点から構造的分割が推奨されます。MPI並列版CABARETが開発され、フェーズ2aでテストされました。CABARETの計算のメインループは、HECToR上で使用可能な如何なるFortran90コンパイラーによってもベクトル化が達成できません。
フェーズ2bの設置により、CABARETはより多くのマルチコアアーキテクチャーへの対応の必要性から、ハイブリッド並列化が実装されました。代表的なサイズのテストケースにおいては、24コアのフェーズ2bでのMPI版CABARETは、クアッドコアのフェーズ2aで示していた性能を下回りました。メインループのマルチスレッド化によるハイブリッド並列化により性能は向上し、CABARETはマルチコアをより効率的に利用可能な状態になりました。
本作業の成果を以下に纏めます:
| 1. | Gambitが生成した非構造グリッドの自動領域分割手法を実装した。そのパーティションは、良好な計算負荷バランスと通信最小化を保証する。このパーティショナーは5.12×10百万グリッドで検証され、現在はHECToRフェーズ2b上で2.05×100百万グリッドの処理が可能である。この手法についてはレポートを纏めた[13]。 |
| 2. | 並列版CABARETは、内部境界(セル面と側面)間のデータ通信をノンブロッキングMPIを用いて実装された。このコードは、元のコードに対して3D後方ステップケースで検証され、HECToRフェーズ2aクアッドコアアーキテクチャーにおけるXT4の250コアを用いて、並列効率72%を示した。 |
| 3. | 新しいコードは、HECToRのXT4を用いて3D後方ステップケースで検証された。 |
また、当初の目的に追加して以下の成果を得ました:
| 4. | フェーズ2bに向けた、ハイブリッド並列版CABARETが実装された。パーティショナーもハイブリッド並列化された。 |
| 5. | 5.12×10百万グリッドの3D後方ステップケースでは、フェーズ2b上の1000コアを用いて並列効率80%を示した。 |
| 6. | 現在は、旧バージョンよりも少なくとも512倍のグリッドを用いたシミュレーションが可能である。それ以下の小さなシミュレーションは、以前は数日かかるものが数分で実行可能になった。 |
8 謝辞
このプロジェクトは、nAG Ltd.が運営するHECToRの分散計算科学および工学(CSE)サービスの基に実行されました。英国の国立スーパーコンピューティング・サービスである、HECToR:英国リサーチ・カウンシル・ハイエンド計算サービスは、リサーチ・カウンシルを代行するEPSRCが管理しています。そのミッションは英国学術界の科学および工学の研究支援です。HECToRスーパーコンピューターは、UoE HPCx Ltd.およびnAG Ltd.のCSEサポートサービスにより管理運営されています。
文献
| [1] | "Balanced Characteristic Method for Systems of Hyperbolic Conservation Laws", V.M. Goloviznin, Doklady Math., 72 (2005), pp619-623. |
| [2] | "A New Efficient High-Resolution Method for Nonlinear Problems in Aeroacoustics", S.A. Karabasov and V.M. Goloviznin, American Institute of Aeronautics and Astronautics Journal Vol. 45 (2007), pp2861-2871. |
| [3] | "A novel computational method for modelling stochastic advection in heterogeneous media", V.M. Goloviznin, V.N. Semenov, I.A Korortkin, and S.A. Karabasov, Transport in Porous Media, Springer Netherlands, 66(3) (2009), pp439-456. |
| [4] | "Compact Accurately Boundary Adjusting high-REsolution Technique for Fluid Dynamics", S.A. Karabasov and V.M. Goloviznin, Journal of Computational Physics, 228 (2009), pp7426-7451. |
| [5] | "CABARET in the Ocean Gyres", S.A. Karabasov, P.S. Berloff and V.M. Goloviznin, Journal of Ocean Modelling, 30 (2009), p155-168. |
| [6] | "Generalized Leapfrog Methods", A. Iserles, IMA Journal of Numerical Analysis, 6 (1986), No 3, pp 381-392. |
| [7] | http://www-users.cs.umn.edu/karypis/metis/ |
| [8] | http://www.labri.fr/Perso/pelegrin/scotch/ |
| [9] | "A Fast and Highly Quality Multilevel Scheme for Partitioning Irregular Graphs", G. Karypis and V. Kumar, SIAM Journal on Scientific Computing Vol. 20 (1999), pp359-392. |
| [10] | http://www.cecill.info/licenses.en.html |
| [11] | "Static mapping by dual recursive bipartitioning of process and architecture graphs", F. Pelegrini, Proceedings of the IEEE Scalable High-Performance Computing Conference (1994), pp486-493. |
| [12] | "A multilevel algorithm for partitioning graphs", B. Hendrickson and R. Leland, Proceedings of the IEEE/ACM SC95 Conference(1995), pp28-28. Also available at http://www.sandia.gov/ bahendr/papers/multilevel.ps |
| [13] | http://www.hector.ac.uk/cse/reports/unstructured partitioning.pdf |
