Paul Roberts, Numerical Algorithms Group Ltd
Michael Lysaght, Department of Physical Sciences, The Open University
1 June, 2012
概要
本プロジェクトにおいて、UKRMol-inスイートコード内のSCATCIプログラムの並列化を行います。大規模なハミルトニアン系に対して、SCATCIはハミルトニアン行列の対角化に最も多くの計算時間を占めるため、本作業はSCATCIプログラムのこの部分の並列化に焦点を当てます。OpenMP/MPIハイブリッドおよびPARPACKライブラリを用いた並列化が、当初の本プロジェクトの計画でしたが、最終的にSCATCIはSLEPc(Scalable Library for Eigenvalue Computations)ライブラリとインターフェイスを取ることになりました。SLEPcはよく知られたPETScライブラリとMPIライブラリを基礎にしています。UKRMol-inスイートは、ターゲット粒子と連続空間軌道関数上の積分計算(およびR行列の有限サイズ補正)と軌道関数の直交化、内殻ハミルトニアン行列の構築と対角化、およびターゲット実行モードでの密度行列計算とそこからのターゲット特性計算、という一連のプログラムから構成されています。このソフトウェアは、Hartree-Fock-SCF軌道あるいは疑似自然軌道および連続系を記述する基底関数を生成するモジュールも含みます。これらは、宇宙物理、プラズマ物理、生体環境の損傷プロセス研究の基礎となります。UKRMol-inは現在、低エネルギー電子衝突により引き起こされるDNA鎖の切断の研究に用いられています。
本プロジェクトは、2011年4月に工数12人月で開始され、2012年5月に完了しました。本作業の責任者はOpen University、物理化学部のJimena Gorfinkiel博士でした。Michael Lysaght博士は当初から2011年11月まで、Paul Roberts博士はプロジェクト完了まで担当しました。
目次
1. イントロダクション
1.1 アプリケーション概要
電子-分子散乱プロセスのモデリングと理解は、宇宙物理、プラズマ物理、生体環境(細胞)における電離に伴う放射線により生起される損傷プロセス等の理解において、基礎的な関連性を持ちます。放射体の低い運動エネルギー(電離閾値以下)においてこうしたプロセスを扱う方法が開発されてきました。特に英国では非経験的な手法で問題を扱うR行列法の利用において先陣を切っています。UKRMol(UK R-matrix polyatomic suite)[1]は、こうした問題の電子記述において世界で最も精度の高いコードの一つです。このコードは、陽電子散乱の研究でも用いられています。医療(処置や診断)での放射線利用は数十年に渡り利用されていますが、ほとんどが経験的かつ巨視的な処方です。しかしながら、放射線に関する近年の生体医療の大きな進歩から、ナノスケールの分子相互作用を含む詳細な記述レベルが増々必要とされています。実験においてはほぼ10年前から、20eVまでの2次電子がDNAを損傷することが確認されています[2]。DNA鎖およびDNA/RNA成分の詳細な研究から、電子衝突メカニズム(解離性電子付着)は、生物学的かつ生理的な変種を導く構造変化を生じる十分な効果を持つことが確認されました。こうした実験で確認された強い活性[3]は、完全弾性プロセスによる理論的な結果とは一致しません。例外はR行列法コードを用いたウラシル[4]および糖分子テトラヒドロフラン[5]研究です。UKRMolはnear threshold ionization[6]のような他の先駆的な研究にも用いられています。
R行列法コードの原子バージョン(PRMAT)は以前のHECToRプロジェクト(M Plummer 博士とA G Sunderland博士による)で移植、最適化されおり、PRMATのPFARM部分をUKRMol-inへインターフェイスする作業と、原子のハミルトニアン構築計算の並列化も行われています(M Plummer博士による)。
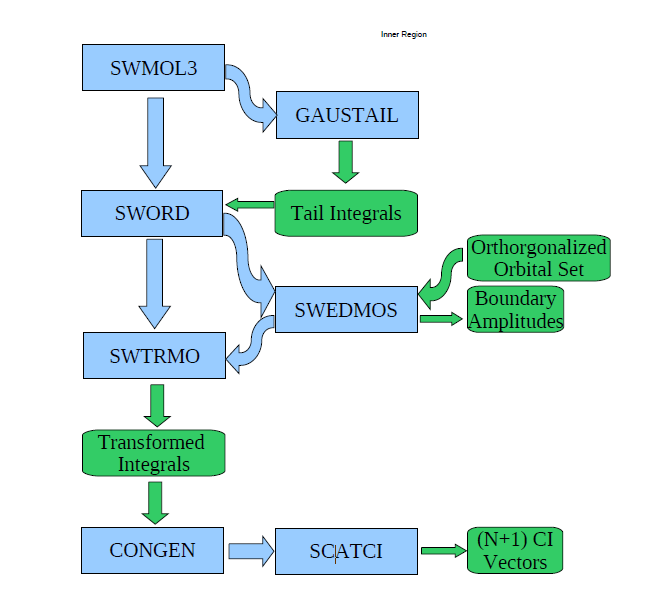
図1: UKRMol-inのメインプログラムのフローチャート
UKRMol-inは図1に示すように、以下に記載する様々な一連のプログラムから成ります:
- 1. ターゲット粒子と連続空間軌道関数上の積分計算(およびR行列の有限サイズ補正)と軌道関数の直交化(図1における、SW*およびGAUSTAILプログラム)
- 2. 内殻ハミルトニアン行列の構築と対角化(CONGENおよびSCATCI)
- 3. ターゲット実行モードでの密度行列計算とそこからのターゲット特性計算(GAUSPROPおよびDENPROP。これは図1に含まれない。)
このスイートには、Hartree Fock-SCF軌道あるいは疑似自然軌道、および連続空間を記述する基底関数の生成モジュールも含まれます。前者については現状は、より洗練された軌道関数を生成する標準的な量子化学コード(特にMOLPRO)を利用しています。後者は通常はそれほど頻繁に用いるものでなく、これらの基底関数はR行列球面半径とターゲットの電荷にのみ依存しています。計算に要するリソースはそれほど多くありません。UKRMolは英国学術界および国外の科学者へはCCPForgeウェブサイトから提供されています[8]。コードは現在、インド、米国、カナダ、フランス、日本のグループで利用されています。ユーザコミュニティがあり、サイト上のツール利用が可能です(メーリングリスト、フォーラム、バグレポート、トラッキングなど)。さらに、UKRMol-inは超短波光パルスによる分子のダイナミクスを扱う時間依存スイートの基盤となるでしょう。
1.1.1 プロジェクト開始時のコードの状況
UKRMol-inは、Open UniversityのLinuxクラスタ、UCLのDell Legionクラスタ、SGIマシンおよびLinuxワークステーション(64GBメモリー、8プロセッサ)で稼働して来ました。最大の実用実行はシリアル実行によるもので、数時間から数か月かかっています(実行時間の99%以上はハミルトニアン行列の対角化にかかっています。チェックポイント機能があり、必要に応じてリスタートが可能です)。メモリーとディスクの必要容量は様々ですが、大きな計算では数十GB程度です。例えば、中規模計算のチミン(C5H6N2O2)のcc-pVDZ既定関数の(14,10)アクティブ空間での計算は、185000×185000程度のハミルトニアン行列が構築されます。SCATCIはハミルトニアン行列構築にCPU時間で422分掛ります。シリアル実行のARPACK対角化を用いれば、5000固有ベクトル計算に対しメモリー33GBが必要とされ、実行に2606分掛ります(CONGENはCPU時間76秒で配置を生成します。これらの時間はIntel Xeon CPU E5540 @ 2.53GHz CPUを用いて、Intel v11.1でコンパイルしたものです)。プログラムのOpenMPバージョンはPavlos Galiatsatos博士により、ARPACK対角化ルーチンを用いて作成されました。この実装で、64GBメモリーのLinuxワークステーション(Xeonプロセッサ)を用いて、524,000次元行列の3000固有値の計算を実行しました(このバージョンはSGIマシンでも実行されました)。これは4コアで2.5倍高速化し、8コアでは4.0倍でした。
SCATCIの現行シリアル版は、Implicitly Restarted Arnoldi/Lanczos Method(IRAM)と呼ばれるArnoldi/Lanczosプロセスのアルゴリズム変形版をベースとする著名なARPACKとインターフェイスを取っています。ARPACKライブラリは逆通信インターフェイスを適用します:この意味は、ライブラリとインターフェイスする際にspMV乗算が必要になることです。SCATCIの現行シリアル版では、spMV乗算がサブルーチンMKARP内に実装されており、対称HN+1行列の下三角部がシーケンシャルアクセスファイル(unordered coordinate (COO) symmetric storage format)からメモリーへ読み込まれます。固有値と固有ベクトルを得るために、ARPACKのDSAUPDサブルーチンを呼び出しと共に収束の繰り返しを行います。これは逆通信インターフェイスが要求され、そこで自製のspMV乗算機構を用いています。
IRAM内で最も時間のかかるのはspMVステージであるため、本作業はこのステージの並列化に焦点を当てます。最後に既存のシリアルspMV乗算のシンプルな高速化について、OpenMPのDOループ指示行によるものを紹介します。ARPACK内の多くのサブルーチンはLAPACKとBLASルーチンとインターフェイスを持つため、IRAM内のこれらのステージには、コンパイル時に適切なフラグを追加してスレッド版のLAPACK、BLASライブラリをリンクして並列にします。
2. プロジェクトの背景
本プロジェクトは12人月で提案されました。目標は以下の通りです:
作業項目1:HECToRへの移植とプログラムの初期動作確認(1人月)
Michael Lysaght博士がHECToR上にてシリアル実行と並列実行を確認します(CCPForgeサイト上の水分子テストが適切)
作業項目2:ハミルトニアン構築の並列化(3.5人月)
作業項目3:スパース行列・ベクトル乗算のOpenMP/MPIハイブリッド並列最適化(3人月)
作業項目4:対角化ステージへのPARPACK実装と最適化(4人月)
作業項目5:レポート作成(0.5人月)
作業項目2,3,4のマイルストーンとして、コード開発の検証として3種のテストを行います。これは将来実行されると予想する異なる特性の計算をカバーします。
- 1.陽電子-HCCH散乱:D2hシンメトリ、l=6までの擬状態と部分波を用いる。
- 2.電子-アデニン散乱:Csシンメトリで、15原子。
- 3.電子-水分子散乱:C2vシンメトリ、6原子、closed-couplingモデル。
これらの系は、OUおよびUCLで詳細に研究されており、必要であれば異なるモデル(より大きな、あるいはより小さなハミルトニアン)も提供可能です。各テストは50万の配置のハミルトニアン(500,000×500,000行列)を含みます。HECToR上での事前テストから、このサイズのハミルトニアンに対するスパース行列・ベクトル積はフェーズ2bのXE6の1つの24コアノードで実行できることが示されました。これはマイルストーン3の基礎となり、そこでは2つのフェーズ2bノードで実行されます。ハミルトニアン構築(マイルストーン2)も1ノード以上での実行が必要になると予想されたので、実行効率は2ノードでテストする予定です。マイルストーン4は1ノードの実行を予定しています。
2.1 作業計画の変更点
Michael Lysaght博士は、Jimena Gorfinkel博士と作業を介した時点で、CCP2がスポンサーであるミーティングMethods and Codes for Atoms and Molecules in Strong Laser Fields in April 2011 [9]に参加しました。その間、彼らは研究関係者と議論をしており、そこでハミルトニアン構築へのPETSc/SLEPc利用の検討を示唆されました。彼らは特にMadridグループ(彼らはMare Nostrumで実行した)からのレポートに印象的な対角化の効率とサイズを見出しました。
SLEPc(Scalable Library for Eigenvalue Problem computations)は、HECToRで利用可能なPETSc (Portable, Extensible Toolkit for Scienti_c Computation)上に構築されたPETScの拡張版です。これはPETScと同等のプログラミングパラダイムを用います。
Michael Lysaght博士はPETSc/SLEPcを詳細に検討し、以下の理由でPARPACKよりも良い選択であると結論付けました:
- 1.データ構造に中立な実装である。並列、シリアル、スパース、稠密なフォーマットで保存された行列問題を解くことが可能。
- 2.実行時に柔軟に処理全体に対して制御可能。
- 3.C,C++,F77、F90で書かれたコードから利用可能で、並列プラットフォームに対して幅広くポータビリティを備える。
- 4.固有値問題ソルバーとしての柔軟性(複数の実装がある)。
- 5.サブルーチンに関するオンラインマニュアル、例題プログラム、ユーザマニュアルといった詳細なドキュメントの存在。
- 6.ARPACKの様な良く知られたパッケージとのシームレスな統合が可能。
こうして作業項目3,4のゴールとして、OpenMP/MPIハイブリッド並列および、PARPACKの利用をPETSc/SLEPc(作業項目2のハミルトニアン構築の並列化にも利用)へ変更して実装することになりました。
SLEPcライブラリはPETScデータ構造を基礎にしており、標準的なMPIを用います。PETScの基本的なデータオブジェクトは、インデックスセット、ベクトルおよび行列の3種です。これを基礎にソルバーオブジェクトの様々なクラスが生成されます。これらは収束閾値など様々なオプションを含む、特定の問題クラスに対する解法に関する全ての情報をカプセル化します。固有値問題ソルバー(EPS)はSLEPcの主要なオブジェクトです。これは標準的あるいは一般化された形式の固有値問題を特定して、パッケージに含まれる全ての固有値ソルバーへ一様かつ効率的なアクセスを提供します。SLEPcには固有値問題を解く様々な手法、Arnoldi/Lanczos法、Jacobi-Davidson法、Krylov-Schur法が備わっており、リスタートの効率性からこの最後の手法がデフォルトで、現状用いられているものです。
3. 実装
3.1 SCATCI修正の概要
R行列の内殻におけるNおよび(N+1)電子ハミルトニアン両方の構築と対角化が、SCATCIプログラム内で生じます。SCATCIの改良作業は、(N+1)電子ハミルトニアンHN+1の構築と対角化の両方のサブルーチンの並列化です。HN+1の次数が大きい場合(10万以上)、UKRMol-inの実行時間の90%がHN+1の対角化に関するサブルーチンで消費されます。HN+1の対角化手法を選択する際に重要なのは、分割R行列法はHN+1の対角化において固有値ペアの約5%のみを必要とし、多くの場合にはHN+1は極めてスパース(約99%のスパース性)であることです。この為、固有値ペアの計算にはKrylovサブ空間ベースの繰返し法固有値ソルバーが選択されています。このような問題では、これは直接法よりも効率的です。こうした固有値ソルバーのコアはスパース行列-ベクトル積(spMV)であり、共有メモリー型や分散メモリー型アーキテクチャ上で並列化可能です。SCATCIは本プロジェクトで改善されますが、そのシリアル版を以降はscatci_serialと参照します。
以降では、SCATCIの修正開発版をscatci_slepcと参照することとします。以下のセクションではMPIおよびPETSc/SLEPcのUKRMol-in、特にSCATCIへの組み込みの詳細を記述します。
SCATCI並列版をscatci_serialとの互換性を保つように開発することに多くの時間を割いています。最終的にはslepc利用スイッチを組み込みました。もしslepc switch == .true.であればハミルトニアン行列並列版が起動し、対角化ステージでSLEPcライブラリが呼び出されます。もし逆にslepc_switch == .false.であれば、scatci_slepcはscatci_serialをエミュレーションします。これは、if文とMPIおよびSLEPc/PETScの呼び出しの組合せで実現しており、この呼び出しには、Makeによるコンパイル時にシリアル版にスイッチされるダミーサブルーチンを使っています。
例えば、SlepcInitialize()を直接呼ぶのでなく、サミーサブルーチンSlepc_Initialize()を呼び出します。scatci_serialを用いるコンパイルの場合は以下のようになります:
subroutine Slepc_initialize(slepc_switch,srank,ssize,scomm) implicit none logical, intent(out) :: slepc_switch integer, intent(out) :: srank,ssize,scomm slepc_switch = .false. srank = 0 ssize = 1 scomm = 0 print*, 'SCATCI run based on serial workflows' end subroutine Slepc_initialize
serial_slepcで用いるようにコンパイルされた場合は以下の通りです:
subroutine Slepc_initialize(slepc_switch,srank,ssize,scomm) implicit none logical, intent(out) :: slepc_switch integer, intent(out) :: srank,ssize,scomm integer, parameter :: master=0 integer (kind=shortint) :: ierr,srank_32,ssize_32 slepc_switch = .true. call SlepcInitialize(PETSC_NULL_CHARACTER,ierr) call MPI_COMM_RANK(PETSC_COMM_WORLD,srank_32,ierr) call MPI_COMM_SIZE(PETSC_COMM_WORLD,ssize_32,ierr) scomm = int(PETSC_COMM_WORLD) srank = int(srank_32) ssize = int(ssize_32) if (srank == master) then print*, 'SLEPc has been initialized' end if end subroutine Slepc_initialize
SCATCIのシリアル版ではハミルトニアンをファイルに書き込みますが、MPI版ではハミルトニアンは複数計算コアで並列に計算され、各コアではローカルなスパースハミルトニアン行列要素は直接PETSc行列(Mat)オブジェクトへ挿入され、続いて固有値問題を定義する演算子であるEPSへ渡されます。様々なオプションがセットされて、問題が解かれた後に最終的に解が得られます。
3.2 ハミルトニアン構築計算の並列化
(N+1)電子ハミルトニアン行列(以降は簡単にハミルトニアン行列と称します)は実対称なので、構築は(対角部を含む)下三角部のみで良く、シリアル版では結果はファイルに書き出されます。これは幾つかの深くネストしたブロックに関するループで処理され、値は行と列のインデックスと共にFortranバイナリーシーケンシャルアクセスファイルへ(下三角のみ)書き込まれます。行列はcoordinate(COO)スパース保存フォーマットに相当する書式でディスク上に書き込まれます。保存形式はCOOフォーマットそのものではなく、行列は非順序で下三角のみ保存されています。
ハミルトニアンは3つのブロックから成り、以降これを連続-連続(CC)、束縛-連続(BC)、束縛-束縛(BB)と呼ぶこととします。
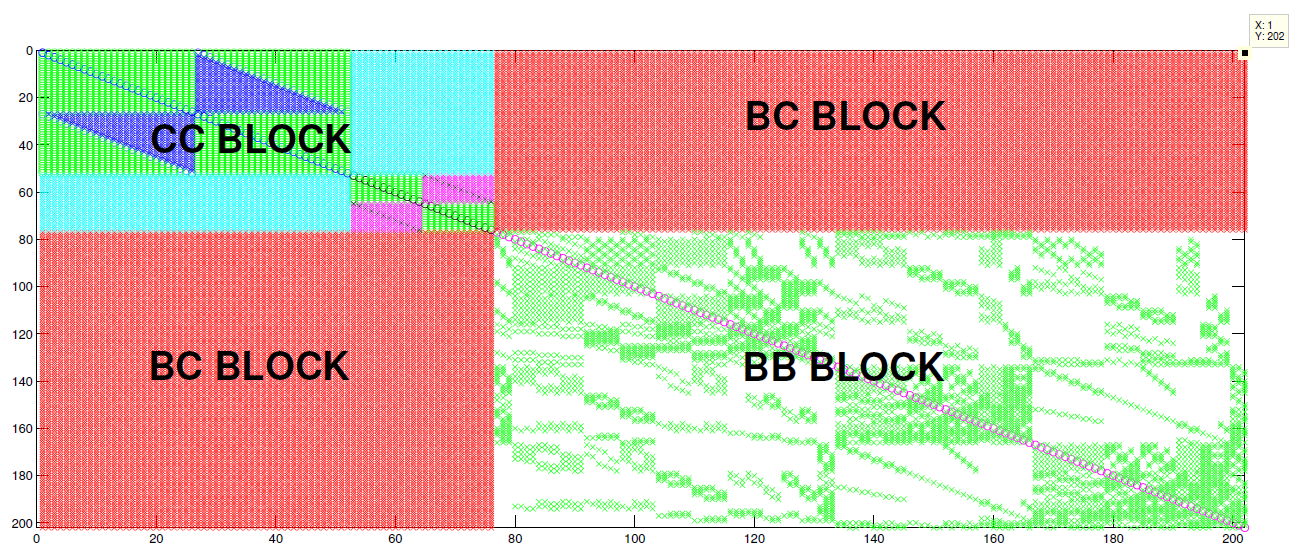
図2: 小テストケースH2Oのハミルトニアン構造。CCブロックの内部”クラス”構造は密構造であることに注意。BCブロックも密である。BBブロックが唯一のスパース部分で非構造的で分子から分子へ変化する。
図2は水分子のハミルトニアン構造を示し、BBブロックのみにスパース構造を見てとれます。BBブロックのスパース性は非構造的で分子から分子へ変化をしています。CCおよびBCブロックは密ブロックです。H2Oは極めて小さなハミルトニアンですが、リン酸やグアニンの様な大きな分子系の場合、BBブロックの次元はCCブロックの次元より数桁大きくなります(リン酸ではCCは700のオーダーで、BBは120,000程度)。よって今後の研究対象分子においてはBBブロックがハミルトニアン行列の大半を占めることになります。こうしたハミルトニアン行列の概要(リン酸のテストケースは通常よりも小さなBCブロックを持ちます)を図3に示します。
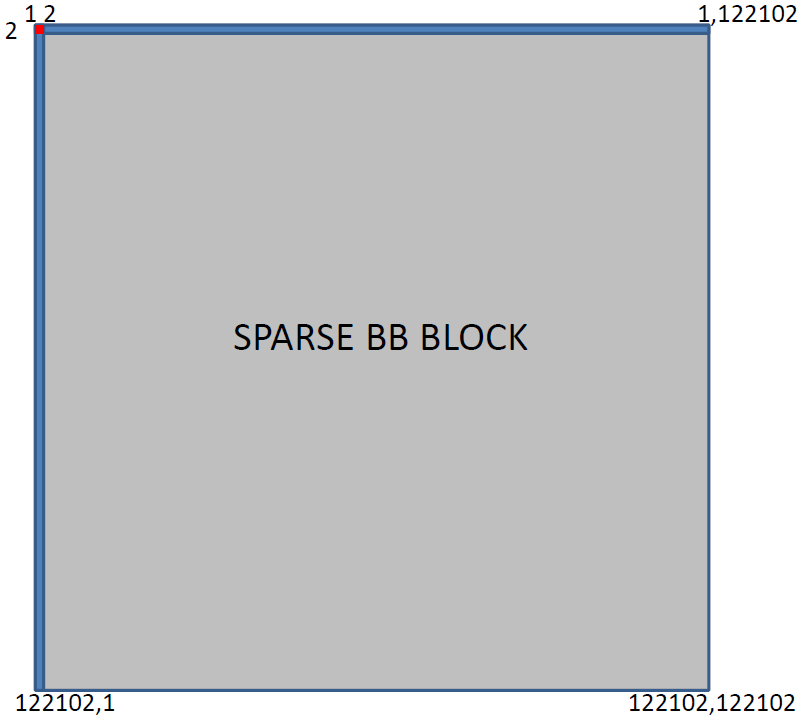
図3: リン酸テストケースのハミルトニアン例。通常はCC(赤)およびBC(青)ブロックはさらに大きいですが、それでもBBブロックよりは極めて小さなものである。
スパース行列要素(行列インデックスと値)をディスクへ保存する代わりに、本プロジェクトでは、その要素をハミルトニアン構築を行うPETScのMatオブジェクト(PETSc行列)へ挿入します。残念ながらこれは直截的に行うことは難しく、PETScではスパース対称行列の上三角部分の順序付けられた行方向の挿入を行わなければなりません。SCATCIではハミルトニアンは下三角行列として構築されることから、CC,BCブロックは最初に処理されるので、PETScのMatオブジェクトへ挿入する前に要素のソートが必要です。
そこで以下において、各ブロックの構成とPETSc行列への挿入のやり方を記述します。
3.2.1 CCブロック
PETScの組み立てステージの間、CC要素は対角化ステージの正しいMPIプロセスに割り当てられるように渡されます。このメッセージ割り当てはPETScにより暗黙的に実行されます。CCブロックは小さく、マスタープロセスは通常対角化の為の全てのCCブロック割り当てで完了する為、このステージは通信負荷は高くありません。
アルゴリズムの観点から、CCブロックの構築は最も複雑なステージですが、次元が小さい為、計算負荷は最も少ないステージです。CCブロックの構築が複雑な理由は”クラス”と呼ばれる高から組み立てられ、各クラスは本質的に異なるアルゴリズムが必要になる為です。こうした背景によりCCブロックの構築の並列化は自明ではありません。しかしながらCCブロック構築にかかるシリアル実行時間はBBブロックに比べて小さい為、ここではCC要素をPETScのMatオブジェクトへの挿入は単一MPIプロセスで行うこととしました。一つのプロセスがCC要素をPETSc Matオブジェクトへ挿入する間に、各プロセスは各々CCブロック全体を構築します。こうする理由は、CCブロック構築で格納される配列があり、それがBCブロック構築の全てのプロセスで必要とされるからです。即ち、BCブロック構築での各MPIプロセスはこれらの配列を必要とします。要するに、CCブロック構築はMPIプロセスで分割されませんが、全てのプロセスは全CCブロックを構築し、一つのプロセスがCC配列をソートしてPETSc Matオブジェクトへそれを挿入します。PETScは対称行列の上三角部のみを受け付ける為、scatci_serialの列番号インデックスは行番号へ割り当てられ行番号インデックスは列番号へ割り当てられます。これはスパース行列の単純な転置です。CC要素のPETSc Matオブジェクトへの挿入の概念図を図4に示します。
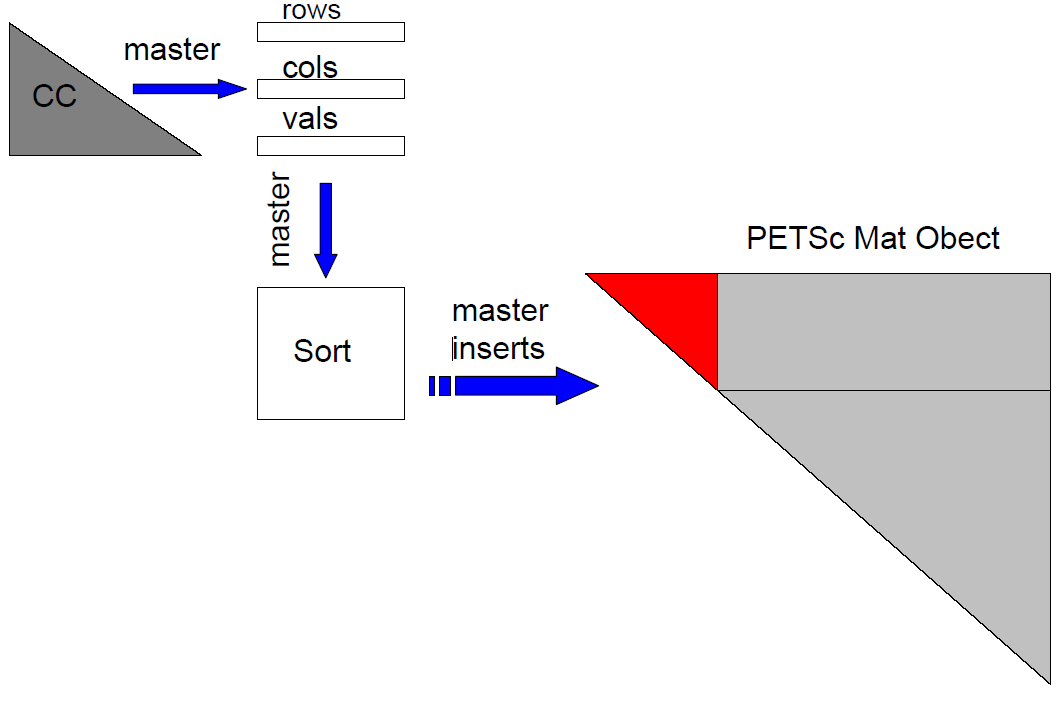
図4: CCブロックのPETSc Matオブジェクトへの挿入の概略。マスタープロセスのみがCCブロックをPETSc Matオブジェクトへ挿入することに注意。PETScは対称行列の上三角部のみを受取るため、挿入前に行と列を入れ替えることが必要。
3.2.2 BBブロック
コミュニケータをbb_commという名前で用意します。このコミュニケータの中で各MPIプロセスは自身に割り当てられた行を構築します。下記プロセスが構築する行は、対角化フェーズでも自身の担当となる為、PETSc組み立てステージでは通信は僅かです。BBブロック構築で実装された基盤のアルゴリズムにより、BB要素は順序付けられて構築されてソートは不要です。図5のプロセス番号はbb_comm内のプロセスIDです。
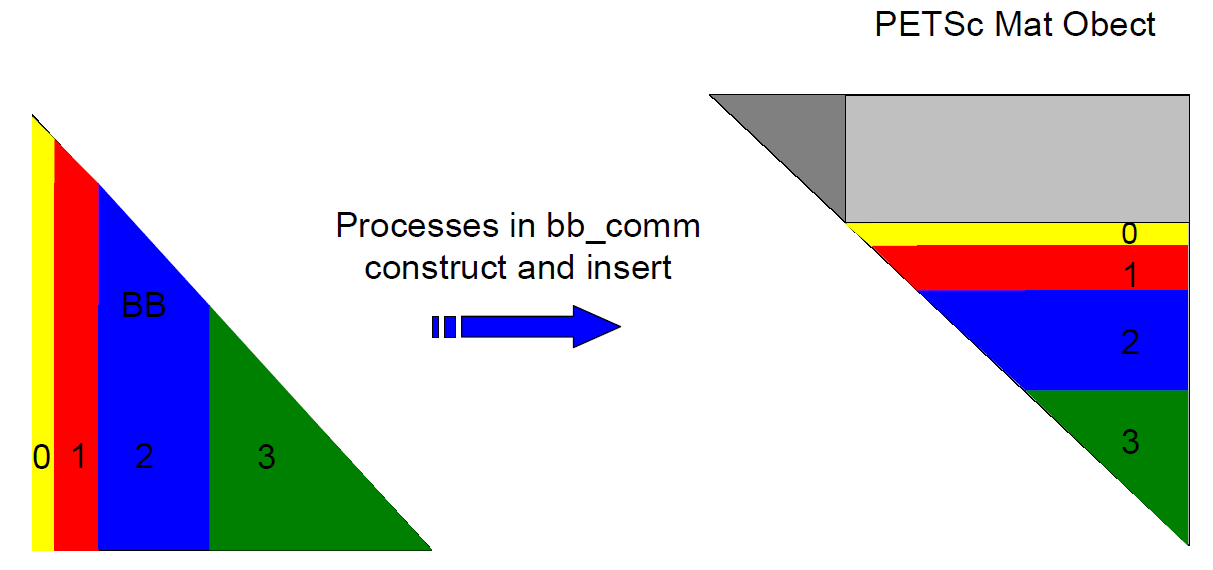
図5: BBブロックのPETSc Matオブジェクトへの挿入の概略。
BBブロックは行列内で最大のブロックであり、本質的にスパースかつ非構造的な部分です。アルゴリズムの観点からは、その構築は極めて直截的で、ネストしたループ内での対称性に基づく条件文に基礎を置いています。運よくBBブロックは順序付けられた形式で列ごとに構築されます。再びPETScは対称行列の上三角部のみを受け付けるので、scatci_serialの列番号インデックスは行番号へ割り当てられ行番号インデックスは列番号へ割り当てられます。BBブロック構築の並列化のために、BBブロック構築に関連するdoループの最外側ループを修正し、各MPIプロセスがそのループの担当部分の範囲を実行するようにします。
CC,BCブロックの構造は行列を構築する前に既存ですが、BBブロックは非構造的で未知なので、行列構築における負荷バランスも未知です。同様にscati_slepcの対角化ステージの負荷バランスは、BBブロック構造の情報が不明なため、ハミルトニアン行列のPETSc Matオブジェクトへの挿入前には不明です。scatci_slepcで採られているやり方では、とりあえず最初にBBブロック構築のネストしたループをスィープします。この初期スィープではBBブロックの構築はせずに、BBブロックの各行の非零要素数を配列に格納します。この初期スィープは並列化されており、各プロセスは同数の行を割り当てられてスィープします。これはPETSC_COMM_WORLD (MPI_COMM_WORLD)の全MPIプロセスを用いて実装されています。各プロセスが自身に割り当てられた行のそれぞれについて非零要素数を配列に格納したら、この配列はマスタープロセスにギャザーされます。一旦これを行えば、負荷バランス機能により各MPIプロセスへ割り当てる行数が決定され、対角化ステージで各MPIプロセスはほぼ均等の非零要素数を扱うことになります。次にBBブロック構築に関するループに対して第二のスィープを実施します。この時は各プロセスは割り当てられた行に対して構築を行い、これら要素を直接PETSc Matオブジェクトへ挿入します。新たに生成されたコミュニケータbb_commに属するプロセスのみがこの第二のスィープを実行します。幸いにもBB要素はPETSc Matオブジェクトへの挿入前にソートする必要はありません。図5はBB要素の挿入の概略です。
3.2.3 BCブロック
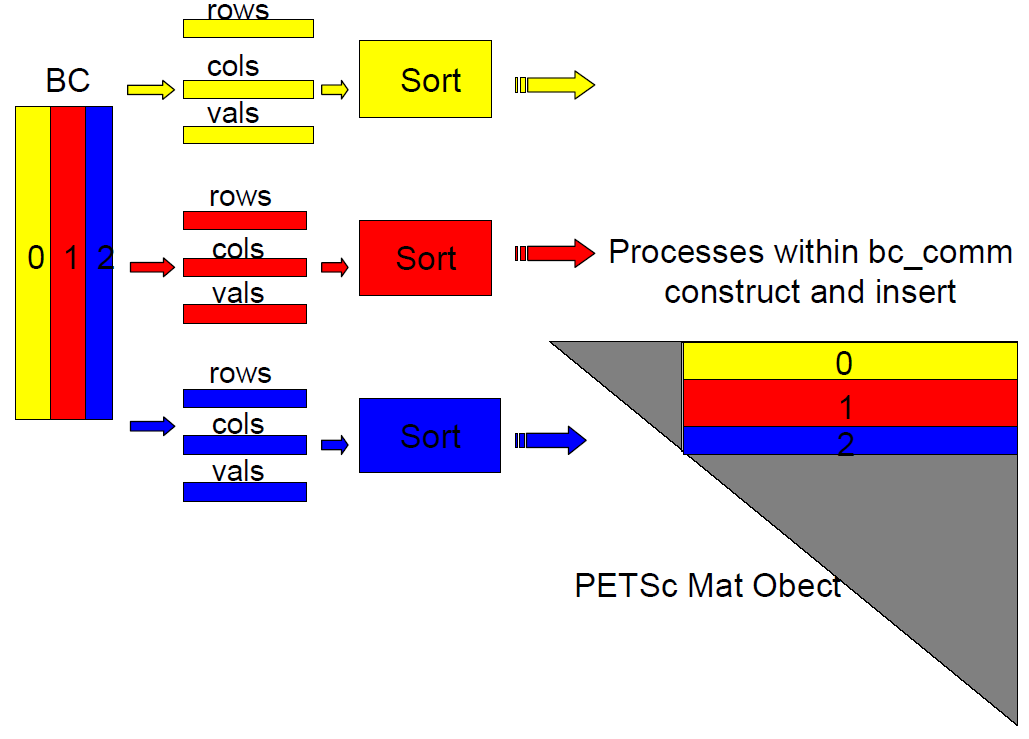
図6: BCブロックのPETSc Matオブジェクトへの挿入の概略。
コミュニケータbc_commがセットアップされたら、各MPIプロセスは保存されるべき配列に割り当て得られた行を挿入します。各プロセスは対角化フェーズで自身が所有することになる行をソートする為、PETSc組み立てステージでは多少の通信が発生します。図6のプロセス番号はbc_commにおけるプロセスIDです。この概念図はBCブロックの構築中に並列に動作するように見えますが、実際には各プロセスは構築に関する全てのネストしたループを実行します。つまりBCブロック構築の作業は分割されません。むしろ構築中に各プロセスはソートされる配列に割り当てられた行を挿入するのみです。
BBブロックは扱いが難しく、BCブロックでは本プロジェクトの間多くの問題が起こりました。最初に、BCブロックが直截的なやり方で並列化されました。BCブロックは行毎に構築されますが、各行内の列は順序付けられていません。BCブロックの構築は最初に、全MPIプロセスに渡り均等な行ブロックで並列化されます。これはBCブロックに関する全てのループの最外側ループを用いた直截的な並列化です。各プロセスは担当するBCの行を構築し、ソートの為にスパース行列の要素を“BC配列”へ挿入します。配列をソートしたら、行列要素はPETSc行列へ挿入されます。このやり方の問題は、最外側ループの並列化は、下三角行列へ行列要素を挿入することになることです。しかしながら先述のように、PETScは上三角行列のみ受け付けます。行列要素の転置は簡単に実行できて、PETSc Matオブジェクトへ挿入が可能ですが、結果的にPETSc Matオブジェクトの組み立てステージはプロセス間に非常に多くの通信が必要になり、極めて高コストになります。実際にBCブロック構築の最外側ループを並列化した場合、各プロセスは対角化ステージで後に担当する要素を構築するわけではありません。重要なのは、各プロセスは(可能な限り) 対角化ステージで後に担当する要素を構築して、PETSc組み立てステージでの通信を用いないようにすべき事です。BCブロック構築を修正しますが、これは非自明な並列化と言えるものです。
現状のやり方は、bc_comm内の各MPIプロセスに対して、BCブロックの構築の全てに関連するループに渡ってスィープして、各プロセスは割り当てられた行のみ挿入します。これは明らかにシリアルなBCブロック構築で、各プロセスは対角化ステージで自身が担当する要素のみを挿入する為、PETSc組み立てステージにおける通信を全くさせないようにするものです。
3.2.4 PETSc組み立てステージ

図7: PETSc行列組み立ての概略。この例では、CCブロックは組み立てプロセスにおいてプロセス0,1,2間で分割されていることに注意。プロセスはPETSC COMM WORLD内のIDで番号付けられる。
このように一旦全ての要素がPETSc Matオブジェクトへ挿入されればPETSc組み立てルーチンが呼ばれます(MatAssemblyBegin() and MatAssemblyEnd())。このフェーズではMPIプロセス間の小さな通信が生じますが、その後、要素のほとんどは対角化フェーズ中にそれらを所有するプロセスによって挿入されます。図6から分かるように、上の例では、CCブロックは複数のプロセスに渡され、マスタープロセスのみがCC要素を挿入し、プロセス1,2は対角化フェーズに対するCCブロック内の要素が割り当てられます。
3.2.5 SLEPc計算ステージ
PETSc Matオブジェクトとして保存されたハミルトニアンのSLEPcによる対角化は、種々のSLEPcルーチンを呼び出すことにより得られます:
!Create eigensolver context call EPSCreate(scomm,eps,ierr) !Set operators. In this case, it is a standard eigenvalue problem call EPSSetOperators(eps,ham,PETSC_NULL_OBJECT,ierr) call EPSSetProblemType(eps,EPS_HEP,ierr) call EPSSetTolerances(eps,tol,PETSC_DECIDE,ierr) call EPSSetDimensions(eps,nstat_32,PETSC_DECIDE,PETSC_DECIDE,ierr) !Solve the eigensystem call EPSSolve(eps,ierr) call EPSGetIterationNumber(eps,its,ierr) !Get some information from the solver call EPSGetType(eps,tname,ierr) call EPSGetDimensions(eps,nev,sncv,smpd,ierr) call EPSGetTolerances(eps,tol,maxit,ierr) !Get the number of converged eigenpairs call EPSGetConverged(eps,nconv,ierr) do i = 0_shortint,nconv-1_shortint !Get the converged eigenpairs: i-th eigenvalue is stored in kr call EPSGetEigenPair(eps,i,kr,ki,Vr,PETSC_NULL_OBJECT,ierr) call VecScatterCreateToZero(Vr,vscat,vout,ierr) call VecScatterBegin(vscat,Vr,vout,INSERT_VALUES,SCATTER_FORWARD,ierr) call VecScatterEnd(vscat,Vr,vout,INSERT_VALUES,SCATTER_FORWARD,ierr) call VecScatterDestroy(vscat,ierr) if (srank == master) then print*, kr + dtnuc(1) if (i == 0_shortint) allocate(hmt(nocsf*nconv),eig(nocsf),dgem(nocsf)) eig(i+1) = kr call VecGetArrayF90(vout,xx,ierr) do j = 1, nkeep hmt(j+(i*nkeep)) = xx(j) end do call VecRestoreArrayF90(vout,xx,ierr) end if end do
この結果はシリアル版の結果とよく一致しています。コードメンテナンスツールの要請の一つとして、これらが一つのバージョンコードである必要があります。つまり、コードに対するいかなる修正も、同じコードがPETSc/SLEPcを用いないデスクトップマシンで用いることができ、SCATCIはUKRMolスィートの1ステップのみ実行されてその結果はUKRMol-outで用いる必要があることから、出力はFortranバイナリーファイルとしてディスクに書き込まれます。シリアル実行コードは書式無のバイナリーシーケンシャルFrotranファイルを書き込みますが、PETScはC言語ベースのためFrotranから直接読み込みが困難なバイナリー形式手法を用いています。残念ながら、このやり方は並列性能に悪影響を与えますが、SCATCIの出力をUKRMol-out内のPFARMへ直接渡す計画があり、これによりこの問題の回避が可能です。
テストは水分子とリン酸に対して行いました(DNA骨格はリン酸で結合し糖分子です)。リン酸のハミルトニアンは122102次の行列で、1.6188の非零要素を持ちます。図8は、シリアル版の結果に基づくSCATCIのOpenMP版の対角化ステージでの性能を示したものです。
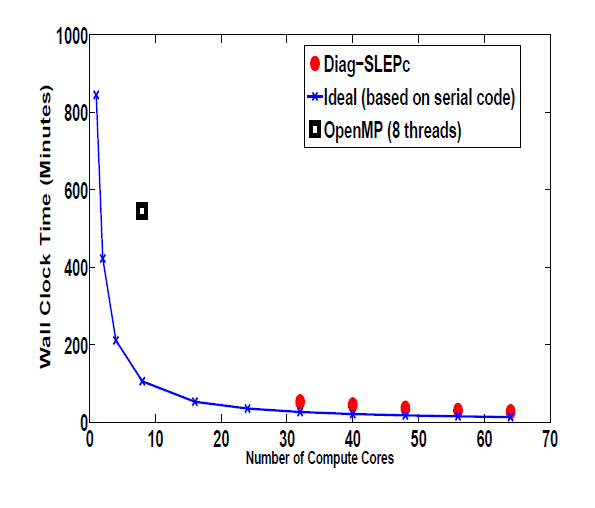
図8: 対角化部の性能
最終的に最大のターゲット問題を解く為には、UKRMolは配列インデックスに64bit整数が必要となりますが、現在のHECToRでは32bit版のPETSc/SLEPcしか存在しません。PGIでは64bitMPIが利用可能ですがPETSC_COMM_WORLDと互換でなくなります。幸いにもデータの並列分割はPETSc/SLEPc/MPIを用いる場合に全てのデータを32bitへキャストすることが可能です。
4. 結論
本プロジェクトの主要な目標は、SCATCIの並列化とHECToRへの移植でした。目的は達成され、HECToRや他の大規模HPCリソース向けのスケーラブルなUKRMol-in並列版が開発されました。ハミルトニアンの構築と対角化ステップは、PETSc/SLEPcの呼び出しにより実装されました。さらに、初期の負荷バランスとUKRMol-inの並列性能改善が行われて、HECToR上の複数ノード上でスケーラビリティが得られ、HECToR上での640プロセッサを用いた実行が行われました。UKRMol-inはさらに大規模な問題サイズを扱うことが可能になりました。この結果はHECToRのUKRMol-inユーザに提供されてCCPForgeに登録されました。
謝辞
このプロジェクトは、nAG Ltd.が運営するHECToRの分散計算科学および工学(CSE)サービスの基に実行されました。英国の国立スーパーコンピューティング・サービスである、HECToR:英国リサーチ・カウンシル・ハイエンド計算サービスは、リサーチ・カウンシルを代行するEPSRCが管理しています。そのミッションは英国学術界の科学および工学の研究支援です。HECToRスーパーコンピューターは、UoE HPCx Ltd.およびnAG Ltd.のCSEサポートサービスにより管理運営されています。
文献
| [1] | J. Tennyson, Phys. Rep.,491, 29-76 (2010) |
| [2] | Boudaiffa B, Cloutier P, Hunting D, Huels M A and Sanche L, 2000 Science 287 5458 |
| [3] | Shukla MK et al and Leszczynski J Eds 2008 Radiation Induced Molecular Phenomena in Nucleic Acids Springer |
| [4] | A Dora, J Tennyson, L Bryjko, and T van Mourik 2009 J. Chem. Phys. 130 164307 |
| [5] | Bouchiha D, Gorfinkiel JD, Caron LG and Sanche L 2006 J. Phys. B 39 975 |
| [6] | Gorfinkiel JD and Tennyson J 2004 J. Phys. B 37 L343; 2005 J. Phys. B 38 1607 |
| [7] | Gorfinkiel J D, Morgan L A and Tennyson J, J. Phys. B 35, (2002) 543. |
| [8] | http://ccpforge.cse.rl.ac.uk/gf/project/ukrmol-in/ |
| [9] | http://www.physics.dcu.ie/ damot/ |
| [10] | http://www.hector.ac.uk/cse/distributedcse/reports/cabaret/ |
