Asimina Maniopoulou and Ian Bush, nAG Ltd.
Ilian Todorov, STFC Daresbury Laboratory
目次
1 イントロダクション
2 作業1:拡張されたVNLスキームの実装
2.1 イントロダクション
2.2 実装
2.3 結果
2.4 現状
2.5 結論
3 作業2:Multiple Time Stepping
3.1 イントロダクション
3.2 実装
3.3 結果
3.4 現状
3.5 結論
4 全体の結論
5 謝辞
1 イントロダクション
DL_POLY_4[1]は、STFCデアーズベリー研究所[2]のI.T.Todorovにより開発された、一般用途古典分子動力学(MD)シミュレーション・ソフトウェアパッケージです。このソフトウェアはモデルの原子レベルの時間発展モデリングのために用いられ、物性科学や、固体化学、生体シミュレーションおよびソフトマター研究において広く利用されています。また、CCP5[3]の後援の元に開発され、英国および世界的に広く利用されています。このソフトウェアは完全な分散データコードであり、空間領域分割、リンクセル、Verletリスト(Verlet neighbour list)[4]、および3Dデアーズベリーフーリエ変換(DaFT)[5]といった手法を用いています。コードの性能は極めて高く、大規模なプロセッサー数に対してスケールします。
本プロジェクトの目的は、DL_POLY_4の効率の改善のための2つの作業から構成されます。最初の作業は、リンクセル・スキーム内のVerlet近隣リスト(VNL)計算の再設計です。これは、一回ではなく複数回の時間ステップ毎に条件付きで更新される、拡張されたVNLの実装と利用をターゲットとします。これはセクション2で記載します。2番目の改善は、multiple time steppingです。これは、Reversible Reference System Propagator Algorithm(REAPA)を用いたシンプレクティック・スキームの実装により、長距離相関のEwaldや短距離分子内相互作用などの高コスト演算の計算回数を削減します。これらによる性能向上はユーザーの指定による条件付の性質です。
以下に掲げる全ての計算は、HECToRあるいはHECToRのテスト開発システム(TDS)上で実施されました。コンパイラーはGNUバージョン4.6あるいはそれ以上を用いました。またコードは特に開発段階においては、様々なクラスターやワークステーションおよび他のコンパイラーでテストされています。
2 作業1:拡張VNLスキームの実装
2.1 イントロダクション
リンクセル(LC)アルゴリズムは、等空間領域分割(DD)を用いて分子動力学計算を並列化する優れた手法です。シミュレーション・セルは同体積の領域に分割され、各領域は1つのMPIプロセスに割当てられます。原子はカットオフと呼ばれる有限の距離内で互いに相互作用し、各領域辺近傍の原子の座標のみが計算すべき原子と通信します。ここで、カットオフは通常領域の辺の長さよりもかなり小さく設定されます。よってLC法は、グリッド上の微分方程式解法で用いられるハロ交換法と共通点を多く持ちますが、それは原子が空間内で不均一に分散し、時間ステップで移動することを扱えるように一般化されたグリッドポイントを用いる点で異なります。各時間ステップにおいてLC法はその領域に特定された原子ペアの全リストを作成するのに用いられます。このリストはVan der Waals力や、金属結合や、短距離EwaldおよびRDF計算と同様の推定といった全ての二体相互作用計算に用いられます。
リストの評価は高コストで、系が静電エネルギー計算でEwald法を用いて計算するかしないかにより、時間ステップ当りの計算コストはそれぞれ、40%あるいは90%相当が必要です。これはアルゴリズム的にメモリーをそれほど大きく使用せずに、DDカットオフを小さな距離(ここではシェルあるいはパディングとして参照します)分大きくする、および更新時点で粒子がどのくらい遠方に移動するかを追跡することにより削減が可能です。各時間ステップ毎にVNL更新後、粒子がある方向にシェル距離の半分以上を移動しているかどうかをテストされます。これが生じた場合にのみリストは更新されます。手順は単純ですが、コードの残りで多くの重要な影響が生じます。その中で最も重大なことは、領域を横切る粒子と関連する分子内原子のDD近隣の通信が、ステップ中にVNLの更新が不要な場合に行われないことです。さらに、ハロ交換やローカルな再配置が不要にもかかわらず、ハロ全体の座標更新が生じます。また、周期境界条件の実装はプログラム全体を通した注意深い検討が必要です。
2.2 実装
手法の背後にあるアイデアは、ポテンシャルのカットオフ長を用いたシミュレーションと、リンクセルの辺長を分離することです。新しいリンクセル辺は、少なくともカットオフ+ユーザー指定のシェル幅の長さになります。この方法により作成されたコードは、少し大きなリンクセルを使用することになります。これは実装だけでなくこの手法の性能に関しても影響を与えます。
実装には以下のステップが要求されます
| 1. | CONTROLファイルからのシェル幅の入力を実装する |
| 2. | DL_POLY_4は、変数rcutをリンクセル辺とポテンシャルカットオフ両方を指定するのに用いている。リンクセルサイズとポテンシャルカットオフを分離する最初のステップは、新規のリンクセル辺を示す変数rlnkを導入することである。この作業は、カットオフとリンクセルサイズがシミュレーションセルサイズと対応させられているルーチン内において特に注意深く行われなければならない。 |
| 3. | Rcutを用いる30以上のルーチンに渡り、それがrlnkと置き換えるべきかどうかを決定する。これはまたルーチンがrcutを両方の意味で使用しているかや、また様々な箇所で引数リストへrlnkを適切に引数として渡すように変更するなど、注意深く修正しなくてはならない。 |
| 4. | 新しい大きなリンクセルに対するVNL生成を実装する。 |
| 5. | コードが正常に動くかレグレッションテストを行う。つまり変数の分離が正しいかどうか、また時間ステップ毎に修正されたVNLの更新が発生する際に正しく動くかということを検証する。 |
| 6. | 粒子の運動追跡のためのデータ構造を実装する。そのデータ構造は、原子の平均二乗変位のような、コード内の他の目的で用いられることを想定して一般的な形で実装されている。DL_POLY_4は完全なデータ分散コードであるため、原子がドメイン間を跨った場合に追加の少量の通信が発生するが、これに対応したトラッキングデータは、原子だけでなくその領域に属するプロセッサーとも通信が発生する。 |
| 7. | シミュレーション中のどの原子が、VNLの更新を必要とするほど遠くまで動いたかを検知する仕組みを実装する。 |
| 8. |
もしVNLの更新が必要ない場合には: a)(場合によりVNLを圧縮する) b)原子を適切な近隣領域へエクスポートするルーチンを呼出す c)領域のハロを更新するルーチンを適切に修正する |
| 9. | 周期境界条件が正しく実装されたままか検証する |
| 10. | 様々なシェル幅で新しいコードのレグレッションテストを行う。 |
yステップ8と9については更に説明をします。ステップ10は採取的な結果のセクションで示します。
ステップ8について、まずはb)とc)から説明します。VNLの更新がされないということは、粒子がどの近隣領域に含まれるかを計算したときの元々のプロセスにとどまっていることを意味し、DL_POLY_4がデータ分散コードであることから、このプロセスはこの情報を持つ唯一のプロセスです(VNLは大きな量であるため大きなオーバーヘッドを発生するため、これがVNLの通信を避ける最も良い方法です)。ここで粒子が領域を跨った場合、いまやそのプロセスが持つ空間領域の外側にあることになり、境界が"ぼやけた"状態になります。元のコードでは、ここで粒子はその近隣領域を持つプロセスと通信することになります。しかしながらそのプロセスは適切なVNLを持たないため、通信すべきではありません。よってVNLのシェル化は、小さいですが重要な通信の減少を伴います。小さいという意味は各時間ステップで領域を跨る原子の数が多くないことを意味し、重要なことは、そのメッセージが短く、そのためにレイテンシーが効くことです。
しかしながら、エクスポートステージは避けられますが、ハロに関してはそうではありません。ハロは隣のプロセスに属する粒子から成っており、座標更新後、これらの粒子はもはや最新でない参照プロセスの値を再通信する必要があります。これは、DL_POLY_4のプロセスが時間ステップ毎に完全に再順序化を実行するという問題を生じます。これは効率性の観点から全く妥当ではありません。よってプロセスAがその粒子を再順序化した後に、適切なデータをプロセスBへ送り、そのハロを更新します。もしそうでなければVNLがプロセスAの元々の順序に従って計算されてしまい、これは適切なものではありません。よってこれを避けるために、リモートプロセス上でそのハロ内のどの粒子が正しいのかという解釈を保証するために、適切な (つまり最後にVNLが更新されたときの) 順序のハロを移送する新たなルーチンを追加します。このハロの座標更新は、粒子の電荷からグリッド電荷へ変換する際の正確な電荷密度のために重要です。言い換えればこのような"ぼやけた"境界は不正確な電荷密度や誤った静電物理量の評価を導きます。
ステップ8の最初のa)のVNL圧縮に戻りましょう。これはVNL利用の最適化の試みです。シミュレーションでかなり複雑な力場を用いると仮定しましょう。このような場合、VNLは、Van der Waalsや短距離Ewaldや他の静電項や、動径分布関数や、種々の金属ポテンシャルなどの様々な項から成ります。これらの各々について、全近隣リスト上のループが必要でしょう。しかしながらシェルにより、多くの原子ペアはカットオフ以上に離れているため、それらの相互作用はゼロになるでしょう。よって場合によっては、完全なVNLからカットオフ以上に離れたペアを全て削除した圧縮されたVNLを、一時間ステップ内で用いる事が便利でしょう。この圧縮されたリストを用いて、上に記した各項を評価すればより効率的になることが期待できます。ですが実際にはその利得はそれほど大きくないことが解りました。その主な要因は以下の点です
- 各項はその独自のカットオフを持つ。圧縮にはそのうちの最大のものを用いなければならず、よって項によってはゼロのままの相互作用が多く残っている。これは、力の評価のループの最内側における、距離に関する条件文を外すことが出来ないことを意味する。
- 圧縮を効かせるには、VNLは多くの項から成るべきで、最内側ループ内の多くのゼロの評価を避けることが出来る。実際には3以上の項を用いる事は稀で、上述の相互作用の幾つかは物理的な観点からコンパチブルでない(例えば静電項と金属結合)。3項では圧縮の最適化には十分でない。
最終的なコードはリストの圧縮を含めていますが、実用計算での全体的な影響は小さいことが判明しました。
ステップ9は上述の領域の"ぼやけ"の結果から得られ、粒子はそれ自身のプロセスの空間領域に明確に存在するというものではありません。元々のDL_POLY_4は、粒子をプロセスに指定された空間領域へ明確に割当てています。この仮定を崩すと、コード内に多くの修正を要し、最も重要なのは如何に周期境界条件を扱うかとそれに纏わる粒子ペアの分離をどう扱うかです。例えば粒子がシミュレーションセルの箱の右側から外へ出て行ったときが問題であり、そこでは拡張されたVNLスキームは、箱の右端のプロセスが持った状態です。元々のコードでは、箱の左端にあるプロセスが受け止めて、適切な格子ベクトル分シフトするようになっています。これは、原子を更新するプロセスはシフト後でなく前の位置に原子を見出し、原子間の距離を不正に評価します。これらは注意深い考察を必要としました。再び、このハロの更新は正確な電荷密度の評価に重要となります。
実装は2,3の面倒な部分を除き直截的なものです。これらの変更による性能への影響は複雑です。次のセクションで性能評価結果を幾つか示しますが、総じていえば以下のように期待されます
| 1. | シェルが十分に広く粒子が十分にゆっくり進む場合は、VNLはまばらに更新されるだけです。よってこのときは性能に利得が得られます。 |
| 2. | まばらに発生するVNL更新では、原子は稀に、また領域のぼやけのためにより多く領域間を跨がります。これはより大きなメッセージサイズのより頻度の低い通信を生じ、何れにせよ効率的な通信とそれによる小さな性能利得を生じます。 |
| 3. | シェルの使用は、VNLを多少大きくします。よってVNL上のループによる力の計算は、小さな性能劣化を生じます。 |
| 4. |
シェルの使用はリンクセルを大きくします。よって、 a)拡張されたハロを含む領域の全粒子はリンクセルでループされるため、よりコスト高になります。これはVNL自身と3,4体項の評価に影響を与えます。 b)より大きなリンクセルはより厚いハロを意味するので、ハロの設定にはより多くの通信が必要になります。 |
つまり1と2が主たる影響となり、性能は向上すると期待されます。
2.3 結果
最初に極めて簡単な例として、4.2Kにおける256,000個のアルゴン原子を考えます。力場はVan der Waals項(Lennard-Jonesポテンシャル)のみで、近隣リストの計算はこの場合比較的高価です。これは、i)力場が単純なため簡単に計算でき、ii)力場が一つしかないため、複数項での近隣リストの使いまわしはありません。よって近隣リスト計算を減らすことが出来て、さらに極低温のため粒子速度は極めてゆっくりしています。この最後の点が意味するのは、近隣リストの再計算が稀にしか生じないことです。これら全てがこの方法のベストケースシナリオになっています。

グラフ1 : アルゴン原子256,000個の場合の効率
グラフ1から、予測が大きく支持されていることが解ります。0.5Åのシェルを用いた場合は、性能はほぼ倍で、VNLの生成は力の評価よりも極めて効果であると期待された通りです。これはまた、VNLが極めて稀に再計算されていることを示しています。0.5Åのシェルにおいは、VNL計算は90%以上スキップされています。
1.0Åのシェルを用いた場合は、性能は劣化しています。これは上で述べたような様々な理由がありますが、最も重要な点は以下の通りです
- 大きなシェルは大きなVNLを意味し、それはポテンシャルカットオフを超えた原子ペアの追加の相互作用を含みます。各時間ステップで要求される、ポテンシャル計算や圧縮でのループの幾つかは、内容にかかわらずより長いリスト上で計算され、シェルが大きければ大きいほどコストは高くなります。
- より大きなセルのために必要なより大きなリンクセルはより厚いハロを持つため、各時間ステップの最後に生じる更新において、より多くの原子において通信が発生します。つまり再び、大きなセルほど計算コストが高くなります。
この簡単な例題から、各シミュレーションにおいて最適なシェル幅が存在するであろうことが期待できます。よってこの手法の性能を最大限引き出すには、計算実験が必要です。これは時間ステップを制限した幾つかの短い実行で、シェル幅を変数とした性能の計測です。著者らは本レポートの最後で、適切な推奨「初期予想値」を示します。
グラフ2はこの事を、シェル幅とMPIプロセス数の関数としてどのシミュレーションが速いかを図示したものです。明らかに0.5Å幅シェルが最高の性能を示しています。
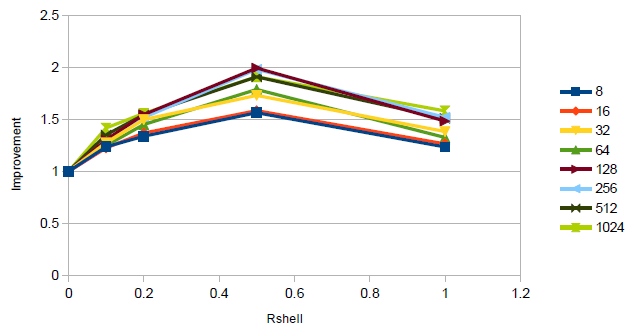
グラフ2 : アルゴン原子256,000個の場合のシェル幅による性能改善
256コアまで性能は向上して元のコードより良いスケール性能を示していますが、性能劣化をするケースも存在します。この理由をはっきりと突き止めることは難しいですが、小さなMPIプロセス数では、VNL更新が実行されないときは領域を跨る粒子と通信する必要がないために通信が減少し、大きなプロセス数では、より厚いハロの通信オーバーヘッドが重要になっているように見えます。
ですが、アルゴンケースの単純さは、他のケースで見られる振る舞いを代表しています。つまり小さなシェルはある地点まではスケール性能を改善できますが、より厚いシェルは性能が落ちます。各ケースの分析は簡単ではなく、最も良いシェル幅は対象系の詳細なダイナミクスに依存しています。これとは別に2つのケースを以下に示します。
最初のケースは500Kにおける塩化ナトリウムの216,000個のイオンです。上記の例と比較して、このシミュレーションはより複雑な力場を必要とし、そこには高コストな静電項が含まれ、VNL更新が比較的低コストになります。さらにこの高温は原子をより運動させ、VNL更新頻度がより高くなると期待されます。つまりそれほど劇的な改善はないであろうことが予想されます。結果をグラフ3に示します。

グラフ3 : NaClの216,000原子の場合の効率
この場合は、0.1,0.2Åシェル幅が約20%の性能改善を示しました。より厚いシェルの線は512コアで中断しています。これはシェルがより大きなリンクセルを要求し、計算領域の最小サイズがより大きくなるためです。よって計算領域内の最大領域数は減少し、これにより使用可能なMPIプロセス数も減少します。このケースでは、リンクセル増大のため1024コアでのシミュレーション実行が可能ではありませんでした。
次のケースは、水のTIP4Pモデルです。232,416サイトを295Kで実行し、水分子は剛体でモデリングしました。結果はグラフ4に示します。

グラフ4 : TIP4Pモデルの水分子の場合の効率
今回はさらに複雑で、最良のシェル幅は明確でなく、コア数に依存していますが、実用上は0.2Åが幅広い領域で良い選択と考えられます。これは約30%あるいはそれ以上の改善を示しています。しかしながらこの曲線を生じる寄与の詳細な分析は困難です。
修正VNL更新コードはDL_POLY_4の標準テストケースで、0.1,0.2,0.5,1.0Åのシェル幅および様々なコア数について検証されました。多くのケースで性能改善が観測され、その平均は20%でした。その中で初期予想値として0.2Åが、常に理想的とは言えませんが、良い選択です。
3,4体力を含む場合のみが大きな性能の落ち込みを示しました。この原因は、この方法で要求される大きなリンクセルまで遡ることが出来ます。何故こうなるかを知るには、2体項のVNLは如何に生成されるかを思い出すことが良いでしょう:シミュレーションセル・ボックスはリンクセルに分割され、この時VNLは、与えられた原子はリンクセル内あるいは近隣のセル内の原子とのみ相互作用するという事実を使って生成されます。このことから、より大きなリンクセルは、VNLの生成に対してより多くの原子を考慮しなくてはならず、より多くのコストが掛かりますが、この影響はシェル化によるVNL生成の機会減少により軽減されます。こうしてVNLは力の計算ループ内で相互作用する原子の選択に用いられました。
3体項に対して同様な手段の利用は可能ですが、3体項の近隣リストは膨大な量のメモリーが必要となります。そこでDL_POLYはリンクセルに対して、実行中に3体項のループ内でその近隣リストを生成するようにしています。このようにしてメモリーの浪費を避けることが出来ますが、3体項ではさらに大きな領域(より厚みのあるハロを含む)を扱わねばならず、それも時間ステップ毎に必要となります。VNLのシェル化は、3体項を用いる問題を解く際には大きな不利益を受け、それは4体項においても同じです。
2.4 現状
このコードは、メインブランチへのマージが完了しており、間もなくユーザーへリリースされます。
2.5 結論
拡張されたVNLスキームは完成しました。多くのシミュレーションでは20%程度の良好な性能改善が観察され、シェル幅の理想的な値には多少の実験が必要ですが、0.2Åが良い初期予想値として示されました。3,4体力を含むシミュレーションの場合は、性能の劣化が観察されました。この場合は、メモリー上の制約からこの新しいスキームの利用は困難でした。
3 作業2:Multiple Time Stepping
3.1 イントロダクション
Multiple Time Stepping法は、それに限りませんが、計算化学の生物化学領域において特に利用されている手法です。シンプレクティックmultiple time stepping:RESPAは、最初にTuckerman, Berne,Martyna[7]により提唱され、後にHumphrey,Freisner,Berne[8]により洗練された研究がなされました。この手法の背後にある考え方は、異なる力場項を異なる時間スケールで進行させることです。例えば、Ewald項の長距離寄与は、分子内の動き、例えば分子振動に比べると極めてゆっくりと変化します。ここで、微分方程式の時間積分では通常、最速の運動が解の数値安定性を保証する時間ステップを決定します(Courant-Fredrichs-Lewy条件[9]を参照してください)。
しかしながら通常の分子動力学においては、時間ステップ毎に力場の全ての項を計算しています。よって正確に分子振動を進行させるには短い時間ステップが要求されますが、同時にその時間ステップでは極めて緩慢にしか動かない長距離力Ewald項も同じ時間ステップで計算させられてしまいます。これでは高価に過ぎるので、RESPA法は、ゆっくり変化する項を指定された時のみに計算し、より速く運動する項には短い時間ステップを使用して、結果の品質をなるべく落とさずに計算します。つまり項によっては毎回計算しないことから、実行時間の削減の効果を期待できます。
RESPA法の数学的基礎は、リウヴィル・プロパゲーターのトロッター展開です。ソフトウェア的には方法は直截的です。MD力場項は幾つかのクラスに分けられ、最も速く動く項(クラス1)は各時間ステップで計算されます。毎n1回目には次に速い項(クラス2)が計算されます。同様に、n2回のクラス2の計算毎(つまりn1*n2回のクラス1計算毎)にクラス3が計算され、以下同様に最も遅い運動項まで続きます。NVEアンサンブルにおいて速度Verlet法と組合せた場合、4クラスに対する(旧来形式の)Fortran疑似コードは以下のようになります(Humphreyらの文献から引用)

図1 : 4クラスRESPA実装の疑似コード
クラス4の力場は長いサイクルに一回だけ計算されるため、これがもし負荷の高い計算であれば、シミュレーション全体の実行時間を削減する効果を持ちます。また、RESPAのパラメーターで、通常のMD実行と異なるものは、上記の単純なn1,n2…のみです。ここで実装したのは4クラスなので、その実行は3つの数字で特徴づけることが出来ます。これ以降、n1=1,n2=4,n3=2の場合は1:4:2と記すことにします。また、multiple time steppingではない通常のMD計算を1:1:1と記します。
multiple time stepping、特に3つの数字はユーザーにより指定されます。数字を大きくすると力場の特定の項の計算が削減されて、計算スピードのより大きな向上を導きます。しかしながらこれはエネルギー保存性をより劣化させるため、どのような場合に適切な値に得るかはユーザー次第です。
3.2 実装
上述したように、ここではHumphreyらの4クラス実装を用います。最初にやるべきことはDL_POLYの力場をクラス分けすることです。ここで、以下のような力場分類をしました:
- クラス1(最速に変化する):コアシェル、拘束原子、調和結合
- クラス2:Tersoffポテンシャル、3体項、4体項、結合角、二面角、inversion
- クラス3:金属結合、Van der Waals項、短距離静電項(Ewaldを含む)
- クラス4(最もゆっくりした):長距離Ewald項
物理的には、クラス1,2が分子内の項で、電子的影響の近似と硬い振動モードを示し、クラス2はより柔らかい振動モード、クラス3,4は分子間相互作用を示します。これらは各々複数のルーチンでカバーされており、複数のやり方でモデル化されています。
この実装は以下のようになります
| 1. | 要求される3つの整数パラメーター領域を用意する。 |
| 2. | これらパラメータをユーザーが設定する仕組みを実装する。 |
| 3. | シミュレーションで力場に対してどのクラスが用いられるかを解析するコードを実装する。 |
| 4. | この分類を使って、指定されたクラスの項のみが計算されるようにルーチンが実装されていることを確認する。 |
| 5. | このやり方をイントロダクションで述べたスキームへ適合させる。 |
これは原理的には直截的ですが、プログラミングには付き物ですが、詳細には困ったこともあります。その一つはクラス分類が完全でない場合がある事です。この場合に最も問題になるのは、圧力一定のアルゴリズムの場合で、これは後程戻りますが、簡単な例は系の重心運動の除去です。これは分子系で重要で、所謂flying ice cubeを避けるためですが、周期系でも大変良いアイデアです。しかしながらこれは系の全力場を必要としますが、RESPAフレームワーク内では、適切な力場が更新されていないことから計算不能になってしまいます。
残る主たる困難は積分器です。通常の全てのシミュレーションをカバーするためには以下の場面が要求されます
- NVE:粒子数一定(N)、セル体積一定(V)、全エネルギー一定
- NVT:粒子数一定、セル体積一定、温度一定
- NPT:粒子数一定、圧力一定、温度一定。等方性・非等方性圧力が必要。
- 剛体:通常は積分器は2つの形式をとり、一つは剛体を扱い、もう一つはそれを含まないより簡潔な形式。
NVTとNPTは様々なやり方で実装可能ですが、それらは強みと弱みを持ちます。DL_POLY_4は各ケースに対して様々な手法をサポートしています。これからの議論は速度Verlet法(VV)を仮定していますが、DL_POLY_4はVVだけでなく、leap-frog Verlet法(LFV)もサポートしています。結果としてDL_POLY_4は60の積分器を用意していますが、基本はRESPA実装において修正が必要です。
事を簡単にするために、RESPA内でLFVを予めサポートしないこととしました。これは、LFV下のRESPAはトロッター展開が動作しないため近似でしかないためで、VV法ではこのような困難が生じません。それでも実装すべき積分器は30あり、テストは膨大な量です。単純な拘束の無いNVEは直截的(イントロダクションで述べたスキームで)ですが、thermostatやbarostatのような拘束条件の追加は、コードをかなり複雑化します。少なくともNVEとNVTに対しては変更は複雑でなく、積分器にどのクラスに座標と速度を正しく更新させるかを伝えることが主にやるべきことでした。ここでは、全てのクラスに対して速度を更新する際に、最速運動項でのみ座標が更新されますが、このことが拘束条件の実装を複雑化しています。その他のクラス依存の変更には、速度の更新における時間スケールがあります。さらに、最速で変化するすラスは常にクラス1とは限らず、シミュレーションでそのような力場を使うかに依存します。
こうした修正作業は、NPTと剛体の場合については作業を完了しませんでしたが、今後やるべきことを簡潔に記します。
圧力一定シミュレーションでは、シミュレーションボックスのサイズは、圧力を保つために変更されます。これは等方性であれば格子パラメーターをスケールすれば良く、非等方性の場合はボックスの形が変更されることになります。これらの変更は全ビリアル係数に依存しますが、RESPAスキームではそれは常に計算可能でないことが問題となります。これに関連して、ボックスの形が変更されると粒子の座標も変わり、積分器の扱いを複雑にします。定圧スキームに特化したRESPAスキーム(例えば、XI-RESPA,XO-RESPA[10])が開発されており、この実装が次に行うべきことです。
剛体の場合は、速度や座標だけでなく角運動量などの粒子には伴わない量を更新しなくてはなりません。RESPAはさて置き、少し複雑化しますが、操作を四元数で表現して、角運動量やその他の量を参照せずに実装する方法があり、DL_POLYではこの手法を用いています。これは大変効率的ですが、数学的な表現として、個別のクラスの力場への適用が力場全体へ一度に適用する場合と同じであることが全く明白でありません(明らかにこれはRESPA shadow Hamiltonianの近似内で正しいです)。この不確定さにより、既存のルーチン群でのRESPAの実装は複雑化してしまい、結果としてこの作業も完了しませんでした。
最終的にNVEと剛体を含まない6つのNVTスキームについて、実装とテストが完了しました。NPTと剛体については部分的に完了しました。これらは1:1:1については正しく実行されましたが、時間の制約で完了は出来ませんでした。
3.3 結果
| RESPA Parameter |
Average Energy |
%Energy Difference |
RMS fluctuations in energy |
RMS/Energy | Time/s | % Time difference |
Timesteps/s |
| 1:1:1 | -9.6965*10^8 | 0.000 | 47.5600 | 0.0000000 | 42.5 | 0.00 | 12.06 |
| 1:1:2 | -9.6965*10^8 | 0.000 | 50.8530 | -0.0000001 | 34.0 | -20.03 | 15.08 |
| 1:1:4 | -9.6965*10^8 | 0.000 | 78.1280 | -0.0000001 | 27.0 | -36.40 | 18.96 |
| 1:1:8 | -9.6965*10^8 | 0.000 | 266.9400 | -0.0000003 | 27.0 | -36.40 | 18.96 |
| 1:1:16 | -9.6965*10^8 | 0.000 | 1072.0000 | -0.0000011 | 26.3 | -38.18 | 19.50 |
| 1:1:32 | -9.6967*10^8 | -0.00825 | 12504.0000 | -0.0000129 | 26.0 | -38.80 | 19.70 |
| 1:1:64 | BREAKDOWN |
表1は塩化ナトリウムの27,000粒子のシミュレーションで、128コア上でのNVEアンサンブルを用いたDL_POLY_4の小規模標準テストです。2048時間ステップ実行され、上記表の測定前に注意深く平衡状態に準備されました。このシミュレーションはクラス3(Van der Waalsと短距離Ewald)と4(長距離Ewald)のみから構成され、RESPAの単純な例題になっています。エネルギーの保存性、実行時間、時間積分の品質がn3の関数として示され、RESPAのパラメーターのみ変化させました。値64まで系統的に2倍の性能に達しました。
平均エネルギーはn3が16まで同じで、その後計算精度が落ちています。これはエネルギーのRMS変動の増加と対応しています:NVEシミュレーションではエネルギーは一定であるべきで、これは運動方程式の時間積分の精度低下を反映しています。実行時間は、n3の増加と共に減少していることが示されています。よってこのシステムは期待通りに、多少の精度低下がありますが、実行時間の削減を達成しており、精度要求とシミュレーション性能向上は反比例しています。RESPAパラメーター1:1:4は精度の点では緩慢な現象を示しますが、実行時間を大きく削減しています。

グラフ5 : 27,000原子NaClのTimestep/s
グラフ5は、計算効率をコア数とRESPAパラメーターの関数として、達成された毎秒当りの時間ステップ数を示したものです。RESPAにより、Timestep/s数、実行時間は良好な改善を示しています。

グラフ6 : 27,000原子NaClの速度向上
グラフ6は、速度向上をコア数とRESPAパラメーターの関数として示しています。この図は32コアまでは完全にスケールしていると仮定しており、特定のパラメーターに関する相対的なものです:すなわち1:1:2カーブは32コアでの1:1:2に対する相対値です。これはRESPAが計算効率を向上させるだけでなく、スケーラビリティーの向上もしていることを示します(グラフ5はこれら2つを合成したものであり、グラフ6は並列スケール性能に焦点を当てたものです)。本ケースは明確な結果を見ることが出来るケースです。その理由として、n3の増加が長距離Ewaldのようなクラス4の回数を減らし、クラス3を強調させているためです。長距離Ewald項は負荷が大きいため、並列の分散メモリーFFTを必要とします。この部分はDL_POLY_4の他の部分よりも、特にクラス3で用いられるハロ交換ベースのリンクセル法に比べてスケール性能が良くありません。こうした理由でスケーラビリティーが改善されました。
次のケースは、ナトリウム/カリウム・二ケイ酸塩ガラスの69,120原子の比較的小規模の例です。再度、この系も注意深く平衡状態へ置かれた後、1024ステップの実行を行いました。前回と同様にRESPAパラメーターの関数としてシミュレーション品質、計算効率、スケーラビリティーを、コア数の関数として考察します。このケースとNaClとの違いは、クラス3,4(前回と同じ内容)を含むだけでなく、クラス2の3体力を含むことです。シミュレーション品質に関連する結果をテーブル2に示します。
| RESPA Parameter |
Average Energy |
%Energy Difference |
RMS fluctuations in energy |
RMS/Energy | Time/s | % Time difference |
Timesteps/s |
| 1:1:1 | -2.0534*10^10 | 0.00000 | 1991.1 | -0.00000010 | 142.068 | 0.00 | 7.21 |
| 1:1:2 | -2.0534*10^10 | 0.00000 | 2020.7 | -0.00000010 | 134.431 | -5.38 | 7.62 |
| 1:1:4 | -2.0534*10^10 | 0.00000 | 2172.2 | -0.00000011 | 132.506 | -6.73 | 7.73 |
| 1:1:8 | -2.0534*10^10 | 0.00000 | 4260.1 | -0.00000021 | 131.832 | -7.21 | 7.77 |
| 1:1:16 | -2.0534*10^10 | 0.00000 | 59690.0 | -0.00000291 | 132.319 | -6.86 | 7.74 |
| 1:2:1 | -2.0534*10^10 | 0.00000 | 2406.0 | -0.00000012 | 120.981 | -14.84 | 8.46 |
| 1:2:2 | -2.0534*10^10 | 0.00000 | 2610.4 | -0.00000013 | 118.981 | -16.25 | 8.61 |
| 1:2:4 | -2.0534*10^10 | 0.00000 | 4650.9 | -0.00000023 | 118.289 | -16.74 | 8.66 |
| 1:2:8 | -2.0533*10^10 | -0.00487 | 61678.0 | -0.00000300 | 118.653 | -16.48 | 8.63 |
| 1:4:1 | -2.0534*10^10 | 0.00000 | 6178.1 | -0.00000030 | 112.206 | -21.02 | 9.13 |
| 1:4:2 | -2.0534*10^10 | 0.00000 | 7754.9 | -0.00000038 | 111.611 | -21.44 | 9.17 |
| 1:4:4 | -2.0533*10^10 | -0.00487 | 73402.0 | -0.00000357 | 111.765 | -21.33 | 9.16 |
| 1:8:1 | -2.0534*10^10 | 0.00000 | 43534.0 | -0.00000212 | 108.165 | -23.86 | 9.47 |
| 1:8:2 | -2.0532*10^10 | -0.00974 | 184360.0 | -0.00000898 | 108.372 | -23.72 | 9.45 |
状況は上記のNaClと同じであることが解ります:RESPAパラメーターの増加は、精度劣化を伴いつつ計算コストを低減します。さらに、3体力を含むクラス2のパラメーターn2の増加は、実行時間と精度へクラス3より大きな効果を示しています。この事はVan der Waalsと短距離Ewald項が長距離Ewaldよりも重要なことを示しています。つまりn2の増加により前者の計算頻度も下がるのに対して、n3は後者にしか影響しません。ジョブの出力はこのことを支持しています。このケースとNaClの両方で、FFTグリッドはほぼ同じサイズです(グリッドサイズは様々なパラメーターの複雑な関数ですが、ここで重要なことは、シミュレーションボックスは両方の系でほぼ同じ体積を持つことです。)。よってFFTの計算時間はほぼ同等ですが、約2.4倍原子数が多く、コードの他の部分のO(N)スケーラビリティーがリニアにコスト増加することにより、クラス3が強調されました。再度、精度が少し劣化しますが、良好な実行時間の改善が示されました(例えば1:2:2や1:4:2ですが、これはシミュレーションに要求される精度に依存します)。

グラフ7 : ナトリウム/カリウム・二ケイ酸塩ガラスの69,120原子のTimestep/s
全てのコアに対してRESPAパラメーターの増加は効率の向上を示しています。

グラフ8 : ナトリウム/カリウム・二ケイ酸塩ガラスの69,120原子の速度向上
同様にn3の増加は、前に述べた同じ理由でスケーラビリティーを改善し、FFTの影響減少とそれがn2の増加により埋没したことを意味します。これは良好なスケールを示すクラス3の実行時間を減少させます。このようにおそらく、より多くの計算が要求されますが、残りの通信と比較すると、スケーラビリティの減少は単に計算が減少したことによります。これらは3体項のクラス2に対してまだ要求されるため、本質的には変更されないままです。
最後のケースは、水中の脂質、1,2-ジミリストイル-sn-グリセロ-3-ホスホコリン(1,2-dimyristoyl-sn-glycero-3-phosphocholine(DMPC))です。これは少し大きな413,896原子で、RESPA用に最初に設計された、生物化学的システムとしてよりふさわしいものです。512時間ステップを実行し、前回と同様に注意深く平衡化したものです。この系は力場に多くの項を用いており、下記の4クラスを用いました:
- クラス1:調和結合
- クラス2:結合角、二面角
- クラス3:Van der Waals項、短距離Ewald項
- クラス4:長距離Ewald項
さらにいくつかの結合が拘束され、時間積分にSHAKE法を用いました。再度シミュレーションの品質を考察して、効率とスケーラビリティーを考察します。
| RESPA Parameter |
Average Energy |
%Energy Difference |
RMS fluctuations in energy |
RMS/Energy | Time/s | % Time difference |
Timesteps/s |
| 1:1:1 | -5.362*105 | 0.00000 | 2.2869 | -0.0000043 | 256.6 | 0.00 | 2.00 |
| 1:1:2 | -5.362*105 | -0.00187 | 2.2996 | -0.0000043 | 234.7 | -8.53 | 2.18 |
| 1:1:4 | -5.362*105 | -0.00187 | 2.5043 | -0.0000047 | 223.6 | -12.86 | 2.29 |
| 1:2:1 | -5.362*105 | -0.00187 | 3.3499 | -0.0000062 | 164.6 | -35.86 | 3.11 |
| 1:2:2 | -5.362*105 | -0.00373 | 3.5209 | -0.0000066 | 153.2 | -40.30 | 3.34 |
| 1:2:4 | -5.361*105 | -0.01492 | 7.8280 | -0.0000146 | 148.2 | -42.24 | 3.45 |
| 1:4:1 | -5.360*105 | -0.03917 | 35.9780 | -0.0000671 | 118.2 | -53.93 | 4.33 |
| 1:4:2 | -5.359*105 | -0.05595 | 35.8130 | -0.0000668 | 117.7 | -54.13 | 4.35 |
| 2:1:1 | -5.361*105 | -0.01306 | 11.6980 | -0.0000218 | 157.6 | -38.57 | 3.25 |
| 2:1:2 | -5.361*105 | -0.01306 | 11.5410 | -0.0000215 | 146.8 | -42.78 | 3.49 |
| 2:2:1 | -5.359*105 | -0.04663 | 28.8950 | -0.0000539 | 111.5 | -56.54 | 4.59 |
| 2:2:2 | -5.358*105 | -0.06528 | 32.7840 | -0.0000611 | 105.9 | -58.75 | 4.84 |
これまでと同様に、RESPAパラメーターの増加は計算時間の減少を生じ、このケースでは特に、精度上の制約が緩ければ、実行時間は半分以下になります。

グラフ9 : 水中のDMPCのTimestep/s

グラフ10 : 水中のDMPCの速度向上
再び、全てのコア数に対してRESPAパラメーターの増加は計算時間の減少を生じています。パラメーターの違いは性能に少ししか効いていません。
3.4 現状
前述のようにNVEアンサンブルと6つのNVTについて実装が完了し、コードの性能は良好な向上を示しました。残る時間積分、NPTと剛体アンサンブルについては、次期プロジェクトに提案されています。
3.5 結論
RESPAが、制約有/無のNVEおよびNVTアンサンブルへ実装されました。コードの性能に関して良好な性能向上が示されました。精度の無視できる劣化を伴いますが、典型的には20%の速度向上を示し、最大2.5倍高速化されました。
4 全体の結論
2種のアルゴリズム上の改善が行われました。多くの方法の中でこれらの手法は共に、演算さもなくば通信の回避をもちいるという同質な側面を持ちます。それはDL_POLY_4内ですでに用いられているアルゴリズムの、よりインテリジェントな実装によるものです。最初に、時間ステップ毎のVerlet近傍リスト再計算を回避するように、リンクセルアルゴリズムを修正しました。次に、各時間ステップにおいて、緩慢に変化する力場項計算を削減するRESPA時間積分手法を実装しました。最初の作業では、各時間ステップ毎に、特定の粒子が別のプロセスの所有権に移されないようにすることで、それに関連する通信を削減しました。RESPAは、力場項がDL_POLY_4で用いられる領域分割に正確に適合しない場所で発生する通信を回避しました。
これらの結果、性能の向上が観測されました。典型的にはこれらは共に、コード性能を20-30%改善しましすが、理想的なケースにおいては2倍以上の完全が可能です。ユーザーにとっては、これらによる入力の変更は僅かですが、最良のシェル幅あるいはRESPAパラメーターを得たい場合には、少量の実験的な試行実行が必要でしょう。
結果として、2つの明らかに異種のアルゴリズムが実装され、その両方はコードの効率に対して類似した利得を示しました。
5 謝辞
著者Ian Bushは、一般的な分子動力学と特にDL_POLYに関する有益な議論をしていただいたBill Smithに感謝します。
このプロジェクトは、nAG Ltd.が運営するHECToRの分散計算科学および工学(CSE)サービスの基に実行されました。英国の国立スーパーコンピューティング・サービスである、HECToR:英国リサーチ・カウンシル・ハイエンド計算サービスは、リサーチ・カウンシルを代行するEPSRCが管理しています。そのミッションは英国学術界の科学および工学の研究支援です。HECToRスーパーコンピューターは、UoE HPCx Ltd.およびnAG Ltd.のCSEサポートサービスにより管理運営されています。
文献
| [1] | http://www.ccp5.ac.uk/DL_POLY/ |
| [2] | http://www.sci-techdaresbury.com/properties/daresbury-laboratory/ |
| [3] | http://www.ccp5.ac.uk/ |
| [4] | I.T. Todorov, W. Smith, K. Trachenko & M.T.Dove, J. Mater. Chem., 16, 1911-1918(2006) |
| [5] | I.J. Bush, I.T. Todorov and W. Smith, Comp. Phys. Commun., 175, 323-329 (2006) |
| [6] | M.R.S. Pinches, D. Tildesley, W. Smith, 1991, Mol Simulation, 6, 51 |
| [7] | Tuckerman, Berne and Martyna, J. Chem. Phys., 97 (3), 1990-2001 (1992) |
| [8] | Humphrey, Freisner and Berne, J. Phys. Chem., 98, 6885-6892 (1994) |
| [9] | Courant, R.; Friedrichs, K.; Lewy, H. (1928), "?ber die partiellen Differenzengleichungen der mathematischen Physik", Mathematische Annalen 100 (1): 32-74 |
| [10] | x Martyna G. J., Tuckerman M. E., Tobias D. J., and Klein M. L., Mol. Phys. 87, 1117(1996) |
