プログラムの高速化・並列化サービスの事例:チューニングレポート：DL_POLY

Ian Bush,
Numerical Algorithms Group Ltd.
Jordan Hill, Oxford OX2 8DR

[2016年2月掲載]

1 イントロダクションおよび背景

DL_POLY_4[1]は、STFCデアーズベリー研究所のI.T.TodorovおよびW.Smithにより開発された、一般用途古典分子動力学(MD)シミュレーション・ソフトウェアパッケージです。このソフトウェアはモデルの原子レベルの時間発展モデリングのために用いられ、物性科学や、固体化学、生体シミュレーションおよびソフトマター研究において広く利用されています。また、CCP5[2]の後援の元に開発され、英国および世界的に広く利用されています。このソフトウェアは完全な分散データコードであり、空間領域分割(DD)、リンクセル(LC)、ベルレリスト(Verlet neighbour　list、VN)[3]、および3Dデアーズベリーフーリエ変換(DaFT)[4]といった手法を用いています。コードの性能は極めて高く、大規模なプロセッサー数に対してスケールします。

リンクセル・アルゴリズム[5]はDL_POLY_4並列化の基盤で、疑似空間領域分割を用いています。シミュレーション・セルは同体積の領域に分割され、各領域は1つのMPIプロセスに割当てられます。ほとんどの原子間相互作用はカットオフと呼ばれる有限の距離内のみで働き、各領域辺近傍の原子の座標のみが計算すべき原子と通信します。ここで、カットオフは通常領域の辺の長さよりもかなり小さく設定されます。LC法は、グリッド上の微分方程式解法で用いられるハロ交換法と共通点を多く持ちますが、それは原子が空間内で不均一に分散し、時間ステップで移動することを扱えるように一般化されたグリッドを用いる点が異なります。

しかしながら、ほとんどの相互作用項はその通りですが、最も重要な例外にクーロン相互作用があります。これは原子間距離rを用いて、1/rのように振る舞います。つまりこれは極めて長距離の相関を生じ、カットオフは不可能です。DL_POLYで最も頻繁に用いられる周期境界条件では、その原子間力の総和の数は周期的なイメージを通して無限大になってしまいます。しかしながらこの問題はEwald和[6]により回避することが出来ます。この手法は、周期系の並進不変性を利用した総和計算の加速手法です。これを実行する伝統的な方法は$N^{2/3}$でスケールします[7,8]。ここでNは対象とする系の粒子数です。さらに最近の手法の中で、Dardenら[9]によるSmooth Particle Mesh Ewald法(SPME)は、高速フーリエ変換(FFT)[10]を用いてN*log(N)でスケールします。DL_POLY_4ではこのSPMEを用いています。

本レポートの残りでは、SPME法の各ステップを説明し、DL_POLY_4がどの様にしてLC法の枠内でこれを利用しているかを述べます。さらに著者が実装した基数2のFFTの元々のDL_POLY実装を記述し、単一基数変換の限界を議論します。この後に、FFTをどのように構造基数による並列変換へ一般化されうるか、およびこれが他のコード部分へのどのような影響を与えるかを記述します。最後に現状のコードの性能とステータスを述べます。

2 Ewald和とSPME

このセクションでは今後に必要となる作業に関してより良い理解のために、SPME法の実行ステップを概説します。より詳細な議論や誤差解析については、上述の文献をご覧ください。
SPME法の主なステップは以下の通りです：

1.量$Q$を生成します。これは単位セル内のグリッド上で定義されて以下の式で与えられます

\begin{eqnarray} && && Q(k_1,k_2,k_3)= \displaystyle \sum_{i=1}^{N} \displaystyle \sum_{n_1,n_2,n_3=-\infty}^{\infty} q_i \\ && && M_n(u_{1i}-k_1-nK_1) M_n(u_{2i}-k_2-nK_2) M_n(u_{3i}-k_3-nK_3) \end{eqnarray}

ここで$q_i$は原子$i$の電荷、$u_{\mu i}=K_{\mu}r_{\mu i}$は原子$i$のスケールされた座標、$ K_{\mu}$はグリッドの次元、$0\leq k_{\mu}\lt K_{\mu}$、$M_n$はn次のカーディナルB-スプライン[11]です。

2.$Q(\boldsymbol{k})$を$Q(\boldsymbol{m})$へフーリエ正変換する

3.$V(\boldsymbol{m})$を構成する

\begin{eqnarray} V(\boldsymbol{m})=\frac{e^{\frac{-\pi^2m^2}{\beta^2}}} {m^2} Q(\boldsymbol{m}) \end{eqnarray}

4.$G(\boldsymbol{m})$を構成する

\begin{eqnarray} && && G(\boldsymbol{m})= \displaystyle \prod_{\mu=1}^{3} |b_{\mu}(m_{\mu})|^2V(\boldsymbol{m}), \\ && && b_\mu(m_\mu)=e^{(2\pi i(n-1)m_\mu /K_\mu)} \left[ \displaystyle \sum_{k=0}^{n-2}M_n(k+1) e^{\frac{2\pi im_\mu k}{K_\mu}} \right]^{-1} \end{eqnarray}

5.$G(\boldsymbol{m})$から$G(\boldsymbol{k})$へ逆フーリエ変換する

6.$G(\boldsymbol{k})$から系の全エネルギーとイオンに働く力を計算する。

このスキームは、DL_POLY_4が用いるデータ分散におけるその利用を容易にさせる重要な性質が2つあります

1.カーディナルB-スプライン$M_\mu$の重要な性質は、$0\lt u\lt n$の範囲でのみ非零であることです。よって原子iによる$Q(\boldsymbol{m})$への寄与を計算する際には、原子近傍の点のみを考慮すれば良いことになります。これは実質的にカットオフを持つ近距離相互作用で、リンクセルアルゴリズムの優れた性質です。

2.フーリエ空間内の全ての計算はローカルです。すなわちその全ては空間内に与えられた点での量の評価になり、グリッド内の別の点の影響はありません。

3 DaFT

つまり重要なのは、系のリンクセル分割を利用する$Q(\boldsymbol{k})$の計算で、この後にフーリエ変換および逆変換を実行することになります。残念ながらFFTW[12]のような標準的な並列3DFFTは、DL_POLY_4で用いられている等空間領域分割でなく、平面内でのデータ分割を要求します。よってFFTWや同様なライブラリーでは大規模なデータの再配置が必要になり、分散データ並列マシンでは極めて効率が悪いプロセスとなります。

その代わりに、数年前に著者が作成したDaFT(Daresbury Fourier Transform)は、DL_POLY_4のデータ分散を直接用いて3D FFTを計算することが出来ます。アイデアの核心は1D FFT各々を並列実行することで、元々のDaFTはフーリエ正変換に基数2のSande-Tukeyアルゴリズムを用いていました。これはdecimation in frequency(DIF、周波数間引き)アルゴリズムで、以下のフーリエ変換です

\begin{eqnarray} X(k)= \displaystyle \sum_{j=0}^{N-1} x(j) e^{\frac{2\pi i}{N}jk} \end{eqnarray}

その内容は、偶数と奇数に対する、半分の長さの２つの変換として記述することが出来ます。

\begin{eqnarray} X(2r)&&=&& \displaystyle \sum_{j=0}^{N/2-1} x(j) e^{\frac{2\pi i}{(N/2)}(2r)j} + \displaystyle \sum_{j=0}^{N/2-1} x(j+N/2) e^{\frac{2\pi i}{(N/2)}(2r)j} \\ X(2r+1)&&=&& \displaystyle \sum_{j=0}^{N/2-1} x(j) e^{\frac{2\pi i}{(N/2)}(2r+1)j} - \displaystyle \sum_{j=0}^{N/2-1} [x(j+N/2) e^{\frac{2\pi i}{N}j}] e^{\frac{2\pi i}{(N/2)}(2r+1)j} \end{eqnarray}

図式的に示せば以下のようにあらわすことが出来ます

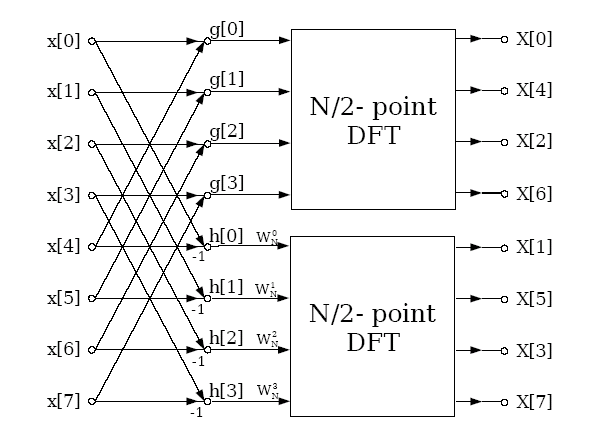
ここで2つのMPIプロセスを用いて、プロセス0が要素0～3、プロセス2が要素4～7を持つようにデータを配置させれば、長さ8の分散メモリーFFTを実行できます。すると2つのプロセスはそのデータを相手に送信して上述のように結合され、プロセスに独立な最終的なFFTを実行するライブラリールーチンが呼び出されます。この分割統治手法は、一つのFFTが2のべき乗の長さを持つ場合に、それを計算する複数のプロセスに関して2のべき乗に一般化可能です。一般にP個のプロセスに対して、プロセッサーペアによるデータ交換および結合の$log_2(P)$個のステージが存在し、各プロセッサーは標準的なライブラリールーチンを用いたN/P長のシリアルFFT実行を行います。

上述のデータ分散は、DL_POLYで用いられている領域分割の1次元の類似である事が見て取れます。これを3次元へ一般化するのは単純です。プロセッサーを$P_x*P_y*P_z$個のグリッド(プロセッサーグリッド)へ分け、x方向の並列1D変換を一斉に実行し、その後y,z方向に対して同様に繰り返し実行します。これはDL_POLYが必要とするFFTアルゴリズムと正確に一致し、結果として初期および最終的なデータ分散を回避できることになります。これが著者の初期の実装で、DL_POLY_3に用いられたDaresbury Fourier Transform (DaFT)です。

残る問題として、DIF法で生成されたベクトルがナチュラルオーダー(natural order)でないことです。これはビット反転（ビットリバース、bit reversed）と呼ばれ、これを並べ替えるのは高コストな通信が要求さるためこのままでは本末転倒です。実際には、DL_POLY_3とDL_POLY_4では、フーリエ空間での演算は上述のようにローカルなので、このことは問題になりません。フーリエ空間での演算はビット反転順で実行され、知らなければならないことはグリッドポイントの値$\boldsymbol{m}$であり、特に他のベクトル$\boldsymbol{m}'$を知る必要はないため、いかなる通信も不要です。さらに力の計算に必要なフーリエ逆変換をdecimation in time (DIT)法であるCooley-Tukey法で実行する際は、入力値はビット反転で与えられますが、最終結果は実空間でナチュラルオーダーとなります。DIT法を図式的に示せば以下のようにあらわすことが出来ます

明らかに、データ交換とシリアルFFT実行のステージが逆になっていること以外は、正変換で用いられた手法と良く似た並列手法が用いられています。さらに逆変換はビット反転の入力を用いるため、2つのFFTステージ間で一切通信を必要としません。

最終的なコード性能は良好であり、[14]で示された通り、スタンドアローン・ルーチンは多くの場合標準的なスラブを用いた3D FFT法よりも性能は低いです。DL_POLY_3のDaFTはほとんどの場合他のDL_POLYよりも優れており、その理由はスラブを用いる手法がデータの再配置という通信がさらに発生するためです。

しかしながら上述のコードは、プロセッサー数を2のべき乗にしなくてはならないという制限があります。プロセッサー数が増えるに従って2のべき乗の値の間隔も広がり、この制約のため、研究者は次の2のべき乗のコア数を用いるためにその計算をスケールアップし、故に計算コストの上昇を招くことになります。将来のHECToRフェーズ2は初期にはノードは2のべき乗のコアを持たないため、研究者は少なくともノードの1つを非飽和で実行せざるを得ません。HECToRはノード単位で用いる事をアナウンスしていますが、これは別の計算リソース浪費となります。本プロジェクトはこれらの問題へ対処することがきっかけとなりました。

他方、プロセッサーグリッドとは異なり、FFTグリッドの次元は2のべき乗の制約を持ちません。その次元は$P_\mu N_{FFT}$で制限されます。ここで$P_\mu$はプロセッサー数で、その添え字はプロセッサーグリッドの次元(x,y,z)です。$N_{FFT}$はシリアルFFTライブラリールーチンが実行する長さです。言い換えれば、この制約はFFTの長さはプロセッサー数の倍数でなくてはならないことを示しています。またこの倍数はシリアルFFTライブラリー関数が許容する長さによって決まります。実際にはこのルーチンにTempertonのGPFAルーチン[15]が用いられています。これは長さに素数列2,3,5を用いてFFTを実行します。つまりDaFTは長さが$P_\mu*2^a*3^b*5^c$の次元のFFTを実行することが出来ます。ここでa,b,cは非零の正整数で、$P_\mu$は2のべき乗です。しかしながらDL_POLY_3は、FFTの次元が2のべき乗でなくてはならないという制約を課しています。この点については現状の作業を記述する場面で再考します。

3D DaFTのアルゴリズムは簡潔なもので、標準的な転置を用いる手法よりもよりシンプルです。プロセッサーグリッドのサイズが$P_x*P_y*P_z$、FFTグリッドサイズが$N_x*N_y*N_z$で与えられた場合は以下のように実行します

x方向の1D FFTを実行する。これらは$P_x$個のコア上に分割され、各コアは$(N_y/P_y)*(N_z/P_z)$数分を実行する。各ステージで全ての1D FFTへ1メッセージのみ送信する必要がある。これは長いメッセージである。
y方向に同様に実行する
z方向に同様に実行する

つまり効率を上げるには、1D FFTをほぼ$P^{1/3}$のコア数までスケールさせれば可能です。ここで、Pはコア総数で、各1D FFTは$P^{1/3}$個のコアに分散されます。

4 DaFT(混合基数)

DaFTの制約はプロセス数の2のべき乗であり、これは現代的な計算システムやDL_POLYユーザーの要請に見合うものではありません。よってDL_POLY_4に対してこの制約の回避のためにdCSEが作業を開始しました。最初の提案は、プロセスグリッド数を因数$2^a*3^{0-2}*5^{0-1}$の形に対応させることでした。これは以下の目的で選ばれました

24コアのノードで構成されるHECToRフェーズ2aのアーキテクチャに適合させる
将来的なアーキテクチャーに向けて生じるであろう修正を許容する
オーバーサイズなシステムを用いなければならないことによる計算リソースの浪費を削減するために、研究者にとって十分な柔軟性を持たせる

実際に実装されたのは、混合基数を用いた領域分割並列FFTです。これはFFT計算に際し如何なるプロセッサー数も許容しますが、アルゴリズムと実装の両面からプロセス数が素因数の小さな整数である場合に最も効率的です。

混合基数アルゴリズムは以下の恒等式を基礎にします：フーリエ変換の長さが$N$で、それが$N=N_1*N_2$へ因数分解できた場合に

\begin{eqnarray} X(k)= \displaystyle \sum_{j=0}^{N-1} x(j) e^{\frac{2\pi i}{N}jk} \end{eqnarray}

上式は下記のように、2つの因数を用いて記述することが出来ます

\begin{eqnarray} X(N_2k_1+k_2)= \displaystyle \sum_{j_1=0}^{N_1-1} \left[e^{\frac{2\pi i}{N}j_1k_2}\right] \left(\displaystyle \sum_{j_2=0}^{N_2-1}x(N_1j_2+j_1)e^{\frac{2\pi i}{N_2}j_2k_2}\right) e^{\frac{2\pi i}{N}j_1k_1} \end{eqnarray}

再びフーリエ変換は2つに分けられています。一つは括弧の中の長さ$N_2$のFTで、もう一つはその外側の総和の、回転因子が追加された長さ$N_1$のFFTです。これら2つのFTは、上述の並列DIFにより計算可能で、2因数でなくとも扱うことが出来るよう一般化可能です。

しかしながら実際に一般化されたプロセス数を効率的に扱うことは、通信パターンが素因数の値に依存するため多少複雑です。その代わりに実用性から、因数をショートとロングの2つのセットに分割することにします。ショート因数は小さい素因数で、プロセッサー数の因数分解はこの因数を高べき数で含むことになります。こうして、変換の各方向でDIF又はDIT FFTアルゴリズムを用いて実行します。ロング因数は大きい素因数で、因数分解には通常は低ベき数で含まれるでしょう。この場合はFFTアルゴリズムは、単純かつ直截的な直交離散フーリエ変換(DFT)と比べて多少の利得を持ち、これらは融合されて単一DFT実行になります。現状はショート因数は2のみをサポートしますが、このコードは他の素因数を簡単に追加できるようになっています。

上記をより明確にするために、ある方向の1D FFTが36コアで実行される場合を考えます。$36=2^2*3^2$であるので、ショート因数は2で、上述の分散FFTアルゴリズムを用い、ロング因数は$3^2=9$で、この場合のFTは単純な単一DFTで計算します。

先述の式においては、ロング因数は$j_2$の総和に対応し、ショート因数は$j_1$の総和に対応します。こうして混合基数正変換は以下のようになります

ロング因数のDFTを実行する
適切な回転因子でスケールする
ショート因数のFFTを実行する

DFT実行には、$N_2$長のDFTを実行するプロセッサー間でデータを巡回する必要があります。この次元のプロセッサー数の因数分解が$P_\mu=S*L$の場合（Sはショート因数の積、Lはロング変数の積として）、S個の変換が存在して、その各変換は関連するデータを持つL個のプロセッサー間と通信してデータをやり取りする必要があります。データ巡回の様々な手法を検討しましたが、二重のバッファーを用いたシストリックループが最も効果的でした。これが良い点は、下記の引用コードのように、計算と通信のオーバーラップを可能にすることです


which = 0
work = a
a = 0.0_wp
rank = desc%rank; rem_rank = rank
Do pulse = 0, desc%size - 1
　t = Exp( Cmplx( 0.0_wp, &
　　( sign * 2.0_wp * pi * rank * rem_rank ) / desc%length, Kind = wp ) )
　If ( which == 0 ) Then
　　If ( pulse /= desc%size - 1 ) Then
　　　Call MPI_IRECV( work2, 2 * Size( work2 ), wp_mpi, down, down, &
　　　　desc%comm, comms_request1, comms_error )
　　　Call MPI_ISEND( work , 2 * Size( work ), wp_mpi, up, rank, &
　　　　desc%comm, comms_request2, comms_error )
　　End If
　　a = a + t * work
　　If ( pulse /= desc%size - 1 ) Then
　　　Call MPI_WAIT( comms_request1, comms_status, comms_error )
　　　Call MPI_WAIT( comms_request2, comms_status, comms_error )
　　End If
　Else
　　If ( pulse /= desc%size - 1 ) Then
　　　Call MPI_IRECV( work , 2 * Size( work ), wp_mpi, down, down, &
　　　　desc%comm, comms_request1, comms_error )
　　　Call MPI_ISEND( work2, 2 * Size( work2 ), wp_mpi, up, rank, &
　　　　desc%comm, comms_request2, comms_error )
　　End If
　　a = a + t * work2
　　If ( pulse /= desc%size - 1 ) Then
　　　Call MPI_WAIT( comms_request1, comms_status, comms_error )
　　　Call MPI_WAIT( comms_request2, comms_status, comms_error )
　　End If
　End If
　which = Mod( which + 1, 2 )
　rem_rank = Mod( rem_rank + 1, desc%size )
End Do

このアルゴリズムは如何なるプロセッサー数でも実行可能で、各方向の1D FFTの長さは対応する次元のプロセッサーグリッドサイズの倍数です。DL_POLY_4では実用上問題は生じていません。グリッドサイズを決める入力はSPME法の最小精度です。FFTグリッドサイズを増やせばSPME法の精度が高くなるので、精度条件と上記の制約が満たされるまで単純にグリッドサイズを増やすことで十分です。実際にオーバーヘッドは小さなものです：HECToRのプロセッサー数の3乗根は約35なので、悪条件ではFFTグリッドは各方向で必要なものよりも大きな34になります。これは以前のバージョンでは2でした。多数のコアを用いたジョブは各3方向で1,000オーダーのグリッドを持ちます。そのオーバーヘッドは明らかに小さなものです。

5 その他の変更

FFTが任意のプロセス数を扱えるよう一般化された後、DL_POLYへの同様の変更が必要になりました。このアプリケーションの前のバージョンは次の事を仮定しています

コア数は2のべき乗
FFTグリッドの次元は2のべき乗

最初のものが主たる制約で、それを外せば2番目の制約も外れます：一般的なやり方は以前のセクションに記述されていますが、すなわち最小の精度条件を満たすサイズを決め、その後に新しいDaFTルーチンの要請を満たすまで、そのサイズを増やしていきます。

最初の制約の除去はコードに多くの変更を与えねばなりません。最大の変更は、任意のプロセス数での領域分割を決めるアルゴリズムの実装です。与えられたコア数に対して、領域分割は以下の条件で選びました

DL_POLYの実行効率を出来る限り向上させる
コードの以前のバージョンの結果を再現する

このようなアルゴリズム開発では、下記の点に注意します

ハロ交換のコードと同様に、メッセージ通信の時間は、単位セルが分離される平行六面体の表面積に比例する
任意のプロセス数に対して、各プロセスが受け持つ体積は、分割に関わらず一定である
よって効率最大化のためには、平行六面体の体積に対する表面積比を最小化しなくてはならず、この問題は、平行六面体の表面積を最小化する領域分割を見つける事へ還元される。

つまりこの問題は最適化問題へ置き換えられます。ここで、同じ表面に異なる領域分割をする際に、少し面倒なことが生じます。これは系の対称性による事象です：例えば16プロセッサーで立方単位セルの4*2*2,2*4*2,2*2*4の領域分割を施した場合、明らかに全て同じ表面が生成されます。ですが、これはより一般的な明白な対称性がない場合にも生じ得ます。このような縮退した領域分割の選択には、以下のコードを用います

プロセスグリッド内の如何なる方向でもコアの最大異数を最小化する因数分解を選択する。これはDaFTの効率を最大化する。
もしこれで縮退を解けない場合は、$P_x\geq P_y\geq P_z$のケースを選択する。

こうしてP個のコアに対する領域分割の選択アルゴリズムは以下のものになります


Calculate the prime factorisation of P
Loop over all Px = Possible factors of P
　Pyz=P/Px
　Calculate the prime factorisation of Pyz
　Loop over all Py = Possible factors of Pyz
　　Pz=Pyz/Py
　　Calculate the S=the surface area of the parallelipipeds
　　If S < the previous best store S, Px, Py, Pz
　　If S = the previous best
　　　If Min(Px,Py,Pz)<Min(Best Px,Py,Pz) store S, Px, Py, Pz
　　　If Min(Px,Py,Pz)=Min(Best Px,Py,Pz)
　　　　If Px< Best Px store S, Px, Py, Pz
　　　　If Px=Best Px and Py < Best Py store S, Px, Py, Pz
　Finish Py loop
Finish Px loop

6 テストと検証

新しいコードは[16]に示された全ての標準DL_POLYテストケースおよび塩化ナトリウムのスーパーセルに対して検証されました。全てのケースで、2のべき乗のコア数での実行は、以前のバージョンの結果を再現しました。2のべき乗でない場合は、系の熱力学的特性は2のべき乗のコアでの実行結果と一致しました。

7 ベンチマーク

216,000個のイオンから成るNaClを用いて、2,000時間ステップの実行でベンチマークしました。これは、実行開始と終了の時間を無視し得るに十分な時間ステップ数となっています。構造のダンプ出力はしていません。このような系の計算に掛かる時間は静電力がほとんどを占めるため、本作業の評価に適しています。特に最も関心のあるのは、プロセッサーグリッドが2のべき乗でない場合のコード性能の劣化に有ります。
図1は、1秒当たりのMD時間ステップ数として計測した性能を示しています。

図1：新しいコードの性能

赤色のカーブが2のべき乗の場合、青色がそうでない場合を示しています。二つのカーブの差は小さいことが見て取れます。よって2のべき乗でない場合の性能劣化の心配は不要と言えます。
表1はこの結果を素因数分解に沿って示した生データです。

Cores	Prime factorisation	Timesteps/s (non power of 2)	Timesteps/s (power of 2)
24	2^3*3	2.08
32	2^5		2.8
40	2^3*5	3.19
48	2^4*3	3.98
64	2^6		5.19
72	2^3*3^2	4.87
96	2^5*3	6.76
120	2^335	7.93
128	2^7		9.1
160	2^5*5	10.8
192	2^6*3	12.34
216	2^3*3^3	13.65
256	2^8		15.85
288	2^5*3^2	15.82
384	2^7*3	20.72
512	2^9		24.48
768	2^8*3	31.18
1024	2^10		36.02
1536	2^9*3	38.84
2048	2^11		44.01

表1：新しいコードの性能

3や5の低いべき乗を含む場合に新しいコードは効果的で、$2^a*3^{0-2}*5^{0-1}$に因数分解されるというコア数の最初の目論見が成り立っています。
新しいコードはDL_POLY_4の標準リリース版の一部としてリリースされています。

8 結論

新しい混合基数の並列FFTがDL_POLY_4へ実装されました。これは、古いFFTと同じくDL_POLY_4の用いる領域分割に正確に適合し、コア数の2のべき乗個の利用という制約を受けません。この新しい柔軟性は性能に小さなペナルティーを持ちますが、これら新しいコードは、HECToRフェーズ2のような最新のマルチコアアーキテクチャーにより適合し、不自然なハード増大を招くコードの制約なしで、研究者は研究を進めることが可能になりました。

謝辞

このプロジェクトは、NAG Ltd.が運営するHECToRの分散計算科学および工学(CSE)サービスの基に実行されました。英国の国立スーパーコンピューティング・サービスである、HECToR：英国リサーチ・カウンシル・ハイエンド計算サービスは、リサーチ・カウンシルを代行するEPSRCが管理しています。そのミッションは英国学術界の科学および工学の研究支援です。HECToRスーパーコンピューターは、UoE HPCx Ltd.およびNAG Ltd.のCSEサポートサービスにより管理運営されています。

文献

[1]	http://www.ccp5.ac.uk/DL_POLY/
[2]	http://www.ccp5.ac.uk/
[3]	I.T. Todorov, W. Smith, K. Trachenko & M.T.Dove, J. Mater. Chem., 16, 1911-1918 (2006)
[4]	I.J. Bush, I.T. Todorov and W. Smith, Comp. Phys. Commun., 175, 323-329 (2006)
[5]	M.R.S. Pinches, D. Tildesley, W. Smith, 1991, Mol Simulation, 6, 51
[6]	P Ewald, Ann. Phys. 64 (1921) 253.
[7]	J. Perram, H. Petersen and S. De Leeuw, Mol. Phys. 65 (1988) 875.
[8]	D. Fincham, Mol. Simulation 13, (1994), 1
[9]	U. Essman, L. Perera, M.L. Berkowitz, T. Darden, H. Lee, L.G. Pedersen, J. Chem. Phys. 103, 19, (1995)
[10]	J.W. Cooley, O.W. Tukey, Math. Comput. 19, 297-301, (1965)
[11]	I.J. Schoenberg, "Cardinal Spline Interpolation", Society for Industrial and Applied Mathematics, Philadelphia, PA, (1973)
[12]	www.fftw.org
[13]	Stoer, J. and Bulirsch, R. Introduction to Numerical Analysis. New York: Springer-Verlag, (1980)
[14]	I.J. Bush, I.T. Todorov and W. Smith, Comp. Phys. Commun., 175, 323-329 (2006)
[15]	C. Temperton, J. Comp. Phys. 52, 1, (1983)
[16]	ftp://ftp.dl.ac.uk/ccp5/DL_POLY/DL_POLY_4.0/DATA/

プログラムの高速化・並列化サービスの事例

チューニングレポート：DL_POLY_4のDaFT FFT

目次

1 　イントロダクションおよび背景

2 　Ewald和とSPME

3 　DaFT

4 　DaFT(混合基数)

5 　その他の変更

6 　テストと検証

7 　ベンチマーク

8 　結論