Dr Sarfraz Ahmad Nadeem, nAG Ltd.
目次
1.イントロダクション
1.1 本プロジェクトについて
1.2 CITCOMの背景
2.初期調査
2.1 背景
2.2 ソースの解読
2.2.1 CITCOMの解読
2.3 注意事項
2.4 その他の事項
2.4.1 data_directory()
2.4.2 date_and_time()
2.5 実装とテストの計画
2.5.1 実装
2.5.2 テスト
2.5.3 最適化
2.5.4 追加テスト
3.マルチグリッド法
3.1 マルチグリッド法
3.1.1 緩和/補正
3.1.2 延長補間/内挿
3.1.3 制限補間/射影
3.2 マルチグリッド・サイクル法
3.2.1 Vサイクル法
3.2.2 Wサイクル法
3.2.3 FMGサイクル法
3.2.4 マルチグリッド法
3.3 計算モデル
3.4 テスト問題
3.5 結果
3.5.1 単純2次元テスト問題
3.5.2 単純3次元テスト問題
3.5.3 複雑2次元テスト問題
3.5.4 複雑3次元テスト問題
3.5.5 結果の纏め
3.6 ポスト処理ツール
3.6.1 CITCOMツール
3.6.2 Gnuplot
3.6.3 Generic Mapping Tools(GMT)
3.7 次期フェーズ作業の検討
3.7.1 メッシュ・リファインメント
3.7.2 延長補間と制限補間の改善
4. リファインメント
4.1 延長補間と制限補間
4.2 局所メッシュ・リファインメント
4.2.1 リファインメント方法
4.2.2 リファインメント準備
4.2.3 リファインメント実装
4.2.4 結果
5. 結論
5.1 作業サマリー
5.2 結果
5.3 今後の改善
1.イントロダクション
1.1 プロジェクトについて
本プロジェクトはダラム大学・地球科学学部Jeroen van Hunen博士および同大・工学部Charles E. Augarde博士により提案されました。目標とされたのは、地殻力学における熱対流問題を解くための並列有限要素法コードであるCITCOMパッケージのマルチグリッド法による性能改善です。このコードはC言語で記述され、MPIライブラリーで並列化されています。
本プロジェクトは12人月の予算が確定し、2009年1月から2010年3月までの計画でした。
本プロジェクトの目的は、収束率向上により並列性能とスケーラビリティを改善することです。この目的のために、既存のVサイクルのみ実装されたマルチグリッド法(MG)に対し、WサイクルとFサイクルを実装することにより改善し、メッシュ・リファインメントやプロセス間通信を含め、アルゴリズム的かつプログラミング的な改善を施します。提案に沿って3つのフェーズを設定しました。最初の初期調査フェーズ1の後に、以下の2つのフェーズでの改善案が提案されました:
- フェーズ2
(a) MGサイクル
既存のVサイクルを改善し、WサイクルとFサイクルも実装する。
(b) スムーシング
既存のヤコビ法ソルバーをガウス・ザイデル法ソルバーへ置き換え、境界ノードに対してblack/redプロセス間通信を実装する(詳細は2章を参照してください)。
- フェーズ3
(c) メッシュのリファインメント
高粘度勾配付近に局所メッシュ・リファインメントを実装する。
(d) 延長補間(prolongation)と制限補間(restriction)の改善
MGレベル間の情報の内挿と移行を改善する。しかしながらこれはこの実装がCITCOMに適合し可能なものかを調査する必要がある。
実装と性能改善の詳細は以降の章で詳細に議論します。
1.2 CITCOMの背景
CITCOMの2次元および3次元カルテシアンバージョンはLouis Moresiにより開発され、後にShijie Zhongにより並列化されて、剛性マトリックスの並べ替えやその半分を保存するような行列演算と共に、プロジェクション法と共にマルチグリッド法の実装によりコード改善がなされました。
2.初期調査
作業の最初のフェーズでは4か月を費やしました。ここでは次のフェーズで必要になるコード実装やテストの計画を行いました。このフェーズでは実装作業は無く、行われたのは、次のフェーズで必要なソースコードに対する修正や改善に必要なCITCOMの調査です。
2.1 背景
このCITCOMパッケージは調査主任自身の持つカルテシアンバージョンのCITCOMのコピーで、元々は彼が2002-2004念の間米国コロラド大学ボールダーの物理学部のポストドクターで働いていた時分のものです。対照的にCITCOMの球面座標バージョンは良く整備されドキュメント化されて、地殻力学ウェブサイトComputational Infrastructure for Geodynamics[5]から入手できるのに対し、このカルテシアンバージョンは初心者にとって十分なドキュメントが有りません。また、ソースコードには比較的コメントは少なく、Doxygen[8]を使ってコードから展開したドキュメントを作成しました。
2.2 ソースの解読
ソースコードにコメントが少ないため、Doxygenから"Call"や"Call by"を作成し、etraceパッケージ[6]を用いて関数呼出しツリーを作成し、CITCOM調査主任との議論等を行いました。
2.2.1 CITCOMの解読
このCITCOMコードは構造メッシュを用いており、2次元では長方形要素、3次元では直方体要素です。これらの要素は2次元では四角形、3次元では立方体で表現出来ます。各次元にその次元の長さに関して適切な要素数が与えられ、各軸での要素サイズは要素数とそのメッシュ全体の長さに依存します。こうした要素は2次元では図2.1、3次元では図2.2のように表現できます。
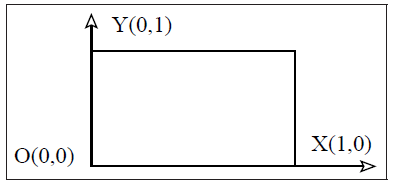
図2.1:2次元における標準的な長方形要素。
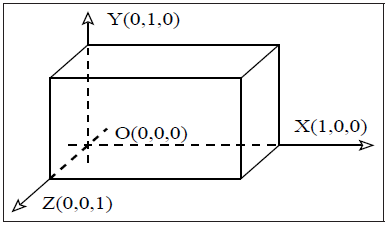
図2.2:3次元における標準的な直方体要素。
本報告は3次元直方体要素に焦点を当てます。これは地球のマントル対流の研究に適したものです。今後の系統的な説明のために、本レポートでは3次元と同様に2次元でも記述をして行きます。CITCOMで用いられる構造メッシュ要素は、通常用いられるカルテシアン座標系である2次元座標(x,y)、3次元座標(x,y,z)という表現ではなく、2次元座標は(x,z)、3次元座標は(x,z,y)を用いています。図2.3でその2次元の長方形要素、図2.4でその直方体要素を示しました。
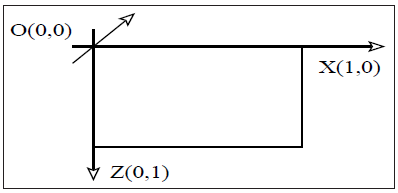
図2.3:CITCOMの2次元における長方形要素。
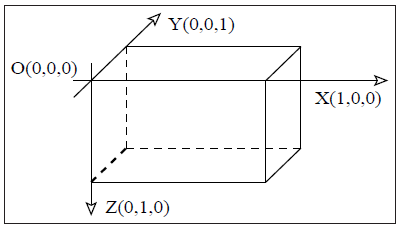
図2.4:CITCOMの3次元における直方体要素。
これをさらに詳しく2次元長方形要素を図2.5、3次元直方体要素を図2.6で示しました。ここでは座標を付けたユニットセルを描いてあり、z座標はz軸の下方を正としています。各要素の局所ノード番号は、2次元では図2.5で示される通り、原点(0,0)から反時計回りに番号付けられます。3次元においては、要素の局所ノード番号は原点(0,0,0)から始まり、正面から始めて次に背面へと図2.6に示されるように番号付けられます。この局所ノード番号は2次元では1から4、3次元では1から8とされ、C言語とは違い0は用いません。CITCOMは全体に渡って0番号が用いられることは有りません。ただし幾つかの例外はあります。
この他の特徴として、通常は0番号の代わりに2つの追加の番号が定義/割当てられます。
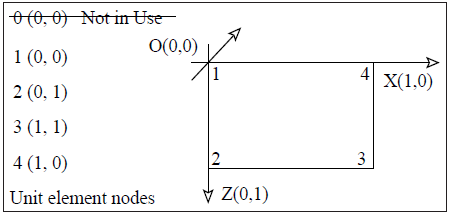
図2.5:CITCOMの長方形要素および局所ノードの関係。
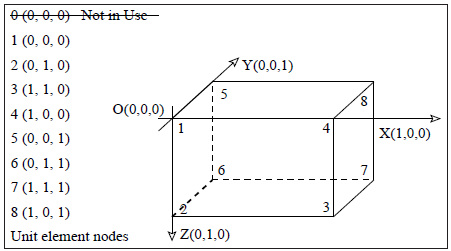
図2.6:CITCOMの直方体要素および局所ノードの関係。
メッシュと地球のマッピングを考える際に、地球表面上に在る要素以外にメッシュ表面要素が無い場合を考えます。言い換えれば、2次元ではX軸に接触する要素、3次元ではXOY平面にある要素のみを、表面要素として考えます。同様に2次元ではX軸上のノード、3次元ではXOY平面上のノードのみを表面ノードとして考えます。具体的には、2次元の場合は図2.7に示したように、要素4は表面ノードでなく、要素7は表面要素となります。要素4は表面ノードを持たず、要素7は10と13という2つの表面ノードを持ちます。つまり表面ノードを持つ如何なる要素も、メッシュ内の位置に関わらず表面上に2つのノードを持つことになります。
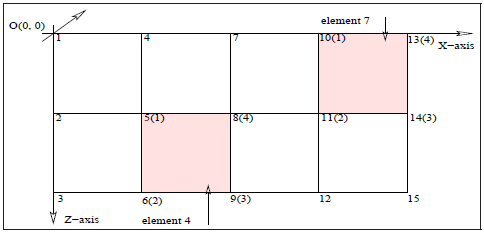
図2.7:8個の長方形要素のCITCOMメッシュ例。
ここで注意したいのは、上述のメッシュ内表面要素に関する記述は、有限要素メッシュの数値計算的な表面のもので、地球科学的な意味ではありません。後者においてはこうした事は明白に良く理解されています。これはただの言い方の問題かもしれませんが、ここではそれを明確に述べて置きます。
要素に対する別の重要な関係として、局所ノード番号付けを全体の番号に対応させることがあります。これはメッシュの結合関係と、メッシュ内の与えられたノードに対する座標間の関係を規定するものです。こうした結合関係は、図2.7で2次元の要素4と7、3次元では図2.8の要素4と15で表されています。
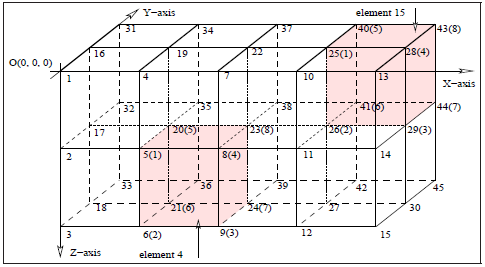
図2.8:16個の長方形要素のCITCOMメッシュ例。
有限要素メッシュに対してこうした関係を規定すれば、要素のパラメーターに対してグローバルノードのようなメッシュパラメーターを計算したり、またその逆を計算するのはそれほど難しくありません。例えば与えられた要素番号に対して、その要素の局所ノード番号に対応するグローバルノード番号や座標を見つけるのは簡単です。逆に、与えられたグローバルノード番号に対して、このノードが属する要素がメッシュ内に幾つ有るかを決めることも難しいことではありません。メッシュ要素、局所ノード、グローバルノード、ノード座標、結合関係などにおいてより複雑な事情は、メッシュのレベルや、メッシュの各レベル内にこれら指標が全て存在しなくてはならない事です。メッシュの各レベルは、要素がリファイン、あるいは再分割される時の深さを表すものです。例えばメッシュ内のある要素が3回リファインあるいは再分割される場合は、その結果の要素はメッシュの3番目のレベルに属します。こうした有限要素メッシュのレベルは、CITCOMのマルチグリッドアルゴリズムで重要な役割を果たします。さらに適切な表現を使えば、こうしたレベルがマルチグリッドアルゴリズムの基本となります。
ここでメッシュの要素とノードの関係に戻りましょう。注意するのは、要素、局所ノード、グローバルノードの番号が0でなく1から始まることです。この要素とグローバルノード番号付けはメッシュ原点から始めて、z軸を増やし、次にx軸を増やし、3次元の場合はさらにy軸を付け加えます。こうした要素とグローバルノードの番号付け増加順序は、要素-ノード関係性や速度、圧力、粘性などのあらゆる量の計算において重要な役割を果たします。
こうした要素とグローバルノードの番号付け順序に加えて、C言語のデータ構造のヘッダーファイルの多くも、CITCOMへのMGアルゴリズム実装に重要な役割を果たします。
2.3 注意事項
CITCOMの実行には、プロセス数あるいはある特定の数列2,4,8,…のプロセス数に対して制限はありません。ですが、CITCOMを正常に動作させrためには幾つかの単純なルールーがあります。このため以下に述べる注意事項を守らねばなりません。
-
x,y,z各方向のmgunitの数は、少なくともx,y,z各方向に対応するプロセス数の2倍が必要です。このmgunit(x,y,z)は各x,y,z方向の要素数を表し、最も粗いレベルの構造有限要素メッシュに対応します。よって、任意のメッシュレベルのx,y,z方向の要素とグローバルノードの正確な数は以下のようにあらわされます:
要素数=mgunit(x,y,z)*2(level-1)
ノード数=mgunit(x,y,z)*2(level-1)+1
これは、CITCOM入力ファイル内で指定されるx,y,z各方向のグローバルノード数を決めるのに役立ちます。ここでは3次元について記載しましたが、2次元でも同様に適用されます。 - CITCOM入力ファイル内で指定するプロセス数は、他のパラメーターと矛盾しない限りにおいて、いかなる値も指定できますが、z方向のプロセス数のみ1としなくてはなりません。
2.4 その他の事項
このセクションで述べる作業は、CITCOMの性能改善には寄与しませんが、コードの解読性や理解のしやすさを高めると考えられる事項について記載します
2.4.1 data_directory()
CITCOMは、必要なパラメーターの読み込みには最初に入力ファイルから読み、入力引数はコマンドラインから読み込みます。入力ファイルには、出力ディレクトリーと出力ファイルのベース名を、入力キーワードdatafileに対して<dirname>/<basefilename>という形式で指定します(ユーザーはキーワードの新規追加、および既存キーワードの変更が出来ますが、コードの不必要な変更のきっかけになることに注意してください)。
CITCOMの実行時には、ジョブ投入前に、CITCOM実行ディレクトリ内に空の出力ディレクトリーを作成します。これを忘れてジョブを実行した場合、ジョブがクラッシュする場合があります。また、既存のディレクトリーが存在する場合は、ベースファイル名が異なる場合でも全てのファイルは上書きされます。
関数data directory()の追加は、こうした望ましくない事故を防ぎます。もはやディレクトリーを作成する必要はなく、実行時に作成されるようになります。もし入力ファイル内で指定した同じ名前のディレクトリーが存在する場合には、現日時と当ジョブのプロセスIDを追加した、<directory>.<yyyymmdd>-<hhmmss>.<pid>というユニークな名称でディレクトリー名は変更されます。この時、このディレクトリーはrootあるいは0プロセスにより作成され、この新しいディレクトリーが作成されるまでは、全プロセスは如何なる出力も制限されます。こうして、計算リソースを無駄にせず、前回の実行結果がユーザーの不注意で上書きされることを防ぎます。
2.4.2 date_and_time()
この関数はC言語のstruct tmを用いて、現在の日時を<yyyymmdd>-<hhmmss>の形式で返すものです。これはdate directory()がディレクトリー名を作成する際に必要になります。
2.5 実装とテストの計画
2.5.1 実装
本プロジェクトで提案された実装作業は以下の作業です:
- 既存のマルチグリッドVサイクルの確認
- マルチグリッドWサイクルの実装
- マルチグリッドFサイクルの実装
2.5.2 テスト
提案したマルチグリッド・サイクルの実装後、比較的小さな中規模サイズのテスト問題に対して、3つのマルチグリッド・サイクルをテストします。ここのでの作業は以下の通りです:
- マルチグリッドVサイクルのテスト
- マルチグリッドWサイクルのテスト
- マルチグリッドFサイクルのテスト
2.5.3 最適化
全てのテスト結果を標準ベンチマークと比較します。結果の精度検証の後に、その実装の最適化として以下の作業を行います:
- マルチグリッドVサイクルの最適化
- マルチグリッドWサイクルの最適化
- マルチグリッドFサイクルの最適化
ここで特に着目するのは、最適化は問題依存なのか、またそうであればサイクルの最適条件を決める特性は何か、という点です。
2.5.4 追加テスト
最適化されたマルチグリッド・サイクルに対して、中規模から大規模テスト、可能であれば超大規模サイズでテストをします。これは、CITCOMの能力に関する試験と、問題それ自身に対する限界に関するものです。
- 中規模から大規模テストサイズに対するマルチグリッドVサイクルのテスト
- 中規模から大規模テストサイズに対するマルチグリッドWサイクルのテスト
- 中規模から大規模テストサイズに対するマルチグリッドFサイクルのテスト
テスト実行と結果検証の完了後、CITCOMパッケージの他の観点から最適化を考察し、良好な性能を期待できる時点で最終的なベンチマークテストを実行します。
3.マルチグリッド法
線形方程式系の解法として、通常は以下の2種のソルバーのどれかを用います。
- 直接法
- 繰返し法
直接法はガウスの消去法を基礎にしており、全ての問題に対して適用できるわけではありませんが、マシン精度で解くことが可能で、良く最適化された場合のコストはO(n2log(n))オーダーです[7](ここで、nは方程式の数/未知数を表します)。
繰返し法はより多くの場面で利用されており、その中でもヤコビ法、ガウス-ザイデル法、共役勾配法が最も広く利用されています。しかしながら、この繰返し法は時間効率が低いため、その克服としてマルチグリッド法が考え出されました。
3.1 マルチグリッド法
マルチグリッド(MG)法は、数値解析法の一種で、通常は偏微分方程式の離散化後に得られる線形方程式系に対するアルゴリズムです。楕円型偏微分方程式はマルチグリッド法の応用の第一候補です。このアルゴリズムは対象グリッドの複数レベルの離散化階層を用います。このアルゴリズムの目的は、複数グリッドレベル、これをマルチグリッドと呼びます、における収束の加速です。この収束加速は以下の順序のステップを踏むことにより達成されます:
| 1. |
粗視化グリッド問題を解くことによるグローバル解の緩和/補正 これはガウス-ザイデルのような繰返し法による高周波誤差を削減する。最も細かいグリッドから始め、最も粗いグリッドへ徐々に移行して計算を進める。 |
| 2. |
細かいグリッドから粗いグリッドへの近似における残差ベクトルの制限補間/射影 これは、例えば平均化等に拠り残差ベクトルを粗いグリッドへ変換する。 |
| 3. |
粗いグリッドから細かいグリッドへの残差ベクトルの延長補間/内挿 これは、粗いグリッドから細かいグリッドへ残差(誤差)の近似を延長補間/内挿し、そこでの補正に用いられる。 |
この3ステップはマルチグリッド法のコンポーネントです。各コンポーネントは以下に簡単に説明します。
3.1.1 緩和/補正
多くの標準的な繰返し法はスムージング性を持ちます[4]。スムージング性は、これらの方法に対して、誤差の低周波あるいはスムースな(振動性のより少ない)成分を残し、高周波あるいは振動成分を効果的に除去します。こうした反復方法は、すべてのタイプの誤差成分を同じく効果的に扱うように改善することができます。緩和処理はより良い初期値を用いる事により改善できます。良い初期値を求めるための良く知られたやり方として、粗いグリッド上で少数の繰返し計算を行う方法があります。粗いグリッドならば未知数も少ないためコストも少なく、粗いグリッドの収束性も僅かに向上することが知られています[4]。さらに、粗いグリッド上で解く利点として、細かいグリッド上のスムースあるいは低周波誤差成分が、粗いグリッド上では振動あるいは高周波誤差成分になることです。言い換えれば、細かいグリッド上での緩和スキームがスムースな誤差でストールするようになった時点で粗いグリッドへ乗り換えれば、この誤差はより振動的に捉えられて緩和スキームはより効率的になります。他のMGコンポーネントと併せて、この仕組みによる効果は問題全体の収束性を実質的に向上させます。
こうした枠組みの中で以下のステップを考えます:
- 細かいグリッド上で近似解へ緩和させる
- 現状の残差ベクトルを計算する
- 計算された残差ベクトルを制限補間演算子として、粗いグリッドへ渡す
- 粗いグリッド上で残差方程式を緩和させて、近似誤差を得る
- この近似誤差を内挿演算子として、細かいグリッドへ渡す
- 粗いグリッド上で得られた近似誤差を用いて、細かいグリッドで得られた近似解を補正する
この処方が補正スキームの概略です。理論的には、収束が停滞あるいは悪化するまで、細かいグリッド上の解を近似する緩和計算は続けられます。実際には、緩和計算は、収束の停滞あるいは悪化を待たずに数回だけ実行します。これはMGスキームのコスト最適化に役立ちますが、最適な緩和ステップ数は問題により変化します。次に緩和計算は、誤差自身の近似値を得るために粗いグリッド上で残差方程式に適用され、次に細かいグリッドで既に得られている近似解を補正するのに用いられます。この細かいグリッドと粗いグリッドを用いた手法は、少なくとも2つのグリッドレベル以上を用いた場合にマルチグリッド法となります。ここでは残差ベクトルは、再精細グリッドから中間的なものを通って最も粗いグリッドまでの、グリッド階層の複数レベルに転送されなければなりません。近似残差(誤差)にも同じスキームが要求されますが、これは粗いグリッドから細かいグリッドへ渡る逆方向となります。これらのグリッド間の転送は、それぞれ制限補間/射影と延長補間/内挿により実行されます。
延長補間と制限補間演算子(およびメッシュ・リファインメント)の改善については本プロジェクトの次のフェーズで計画しており、ここではその基本的な機能のみを示します。
3.1.2 延長補間/内挿
マルチグリッド法における延長補間/内挿とは、近似誤差を粗いグリッドから細かいグリッドへ転送するのに用いられる演算子です。次数に制限はありませんが、最も簡単には例えば線形内挿補間として効率的な動作をします。
3.1.3 制限補間/射影
内挿演算子は近似誤差を粗いグリッドから細かいグリッドへ転送するのに用いられますが、細かいグリッドから粗いグリッドへ残差ベクトルを転送するこの逆演算子は制限補間/射影演算子と呼ばれます。こうした演算子の最も解りやすい例は単射と呼ばれるものですが、より複雑な重みを持つ演算子も存在します。
3.2 マルチグリッド・サイクル法
フェーズ2で実装されたCITCOMのマルチグリッド法をこのセクションで記述します。最初にCITCOMに実装された手法はマルチグリッドVサイクル法およびマルチグリッドWサイクル法です。次の2手法はフルマルチグリッドあるいはFMG法をして知られるFサイクル法です。以降、FMG法内のVサイクルとWサイクルを、それぞれFMG(V)、FMG(W)と参照することとします。
3.2.1 Vサイクル法
Vサイクル法は、最も細かいグリッドから始め、緩和ステップを繰り返し、その後残差ベクトルが計算されて、次の粗いグリッドへ制限補間演算子として渡されます。この手続きは、(最も細かいグリッドに比べて)グリッド数が比較的少ない最も粗いグリッドが得られるまで繰り返されます。その後、延長補間演算子で転送されたより細かいグリッドへの補正を計算しながら、最も細かいグリッドまで引き返します。この手続きは最も細かいグリッドが得られるまで繰り返されます。こうしてVサイクルの繰返しが完了します。Vサイクルの繰返しの様子を図示したものが図3.1です。

図3.1:マルチグリッドVサイクル法。
Vサイクル法が完了した後に、問題全体の収束性を検証します。もし事前に決めた収束条件満足されれば、手続きは終了します。もしそうでなければ、Vサイクル法は収束条件を満たすまで、言い換えれば手続きが完了するまで繰り返されます。
3.2.2 Wサイクル法
WサイクルはVサイクルと似て、緩和、制限補間および延長補間とそれらの機能が関与しています。唯一の違いは、Vサイクルの繰返しと収束判定を2回繰り返すことです。このWサイクルを図3.2に示します。
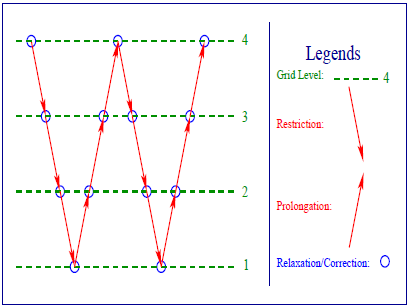
図3.2:FMG(V)サイクル法。
3.2.3 FMGサイクル法
フルマルチグリッド(FMG)における、Vサイクル法によるFMG(V)法とWサイクル法によるFMG(W)法はそれぞれ、Vサイクル法とWサイクル法に似ています。その違いは、繰り返しにおいてVサイクルとWサイクルの場合における全てのグリッドレベルを含むことです。これは最初に最も粗いグリッド2つの間で繰り返され、最も細かいグリッドに到達するまで、中間のグリッドに対して同じ処理をするように拡張されています。言い換えれば、Vサイクル(FMG(V)法における)は2つの最も粗いグリッドから始め、段階的に次の細かいグリッドへ拡張して、全てのグリッドレベルで行うものです。これをFMG(V)法と呼び、その様子を図3.3で示します。FMG(W)法は基本的にはFMG(V)と違いはありませんが、セクション3.2.2で示したようにVサイクルに対するWサイクルのような、その繰返しを含みます。
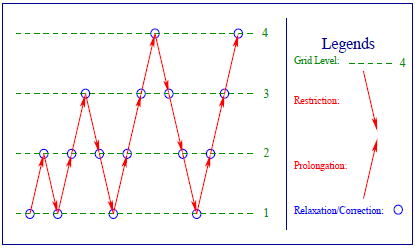
図3.3:FMG(W)サイクル法。
3.2.4 マルチグリッド法
以上を纏めると、問題に応じて以下の4つのマルチグリッド法が可能です。
| 1. | マルチグリッドVサイクル法 |
| 2. | マルチグリッドWサイクル法 |
| 3. | FMG(V)法 |
| 4. | FMG(W)法 |
3.3 計算モデル
有限要素法ベースコードCITCOM[11,12,15]は、温度および密度と粘度に依存する組成を持つ流体を解きます。支配方程式は質量、運動量、エネルギーおよび組成に対する保存則から記述されます:
\begin{eqnarray} \nabla \cdot \vec{v} & = & 0 \tag{3.1} \\ \nabla \tau + \nabla p & = & \Delta \rho g \hat{z} \tag{3.2} \\ \frac{\partial T}{\partial t}+(\vec{v} \cdot \nabla)T & = & \nabla^2 T+H \tag{3.3} \\ \frac{\partial C}{\partial t}+(\vec{v} \cdot \nabla)C & = & 0 \tag{3.4} \end{eqnarray}
ここで、$\vec{v}$は速度場、$\tau$は還元応力場、$p$は還元圧力場、$\Delta \rho$は温度$T$と組成$C$に依存した相対密度、$g$は重力、$\hat{z}$は鉛直方向の単位ベクトル、$t$は時間、$H$は熱生成比です。MG法はストークス方程式(3.1)と(3.2)の解法として用い、温度式(3.3)は単純な前進差分の陽解法、組成式(3.4)はトレーサー法で解きます。式(3.1)と(3.2)は離散形式では以下のようにあらわすことが出来ます:
\begin{eqnarray} Au+Bp=f \tag{3.5} \\ B^Tu=0 \tag{3.6} \\ \end{eqnarray}
この連立方程式はUzawaの繰返し手法で解かれ、式(3.5)は、各MGレベルにおいてガウス-ザイデル法を用いられ、最も粗いグリッドでは共役勾配法で解かれ、式(3.6)は制約条件として扱われます。
3.4 テスト問題
支配方程式(3.1-3.4)に対して、4つの代表的なテスト問題を考えます。これには2次元および3次元の、以下のような地球のマントルや岩石圏に関連する地殻力学問題をカバーします:
- マントル対流
- 沈み込み帯
- マントルプルーム
4つの代表テスト問題は以下のものです:
| 1. | 「単純2次元テスト問題」:時間依存の(レイリー・ベナール)対流を解きます。一定粘度で矩形(1/h=1)を考え、上端で温度0、下端でΔTとして、内部の熱発生はないものとします。これは十分長い実行では、適切な粗いメッシュを用いても数千ステップ掛かり、より細かいメッシュではさらに多くのステップを必要とします。この計算はRa<106であれば安定状態となります。両サイドで対称性が反映され(∂T=0)、ボックスの全境界でせん断応力は0となります。レイリー数はRa=αgΔTH3/κv=104[2]です。ここでhはマントル対流に対しては100から1000キロメートルのオーダーになります。 |
| 2. |
立方体(1/h=1)の場合の、時間依存の(レイリー・ベナール)対流を解きます。一定粘度、上端で温度0、下端でΔTとして、内部の熱発生はないものとします。十分長い実行では、適切な粗いメッシュを用いても数千ステップ掛かり、より細かいメッシュではさらに多くのステップを必要とします。この計算はRa<106であれば安定状態となります。x方向の側壁で対称性が反映され(∂T=0)、立方体の全境界でせん断応力は0となります。レイリー数はRa=αgΔTH3/κv=104[2]です。ここでhはマントル対流に対しては100から1000キロメートルのオーダーになります。 この3次元テスト問題は上述の2次元問題を拡張したもので、四角形をy方向へ伸ばして立方体にした、「単純3次元テスト問題」です。 |
| 3. | この「複雑2次元テスト問題」は「単純2次元テスト問題」の拡張版で、沈み込み帯の重要な地殻力学過程を表します(2つの岩石圏あるいは岩盤/プレートが出会い、一方が相手の下に沈み込みます)。これは、大規模かつ急激な粘度変化を扱っています。このモデル化に用いるのは、温度依存粘度(冷たいと固くなる)η=A(E*/RT)を用います。ここで、E*はマントル物質の活性化エネルギー(約400kJ/mol)、Rは気体定数、Tは絶対温度です。この粘度は、温度Tがマントル温度1350℃から地表付近の0℃に至るまでに、オーダーが30以上増加します。このような粘度の大きな変化は正しくモデリングするのに実用的でないため、粘度の最大値を高温マントルの粘度(これを参照粘度にします)の103から105倍に制限します。ηは計算中に更に大きく変化するため、ストークス方程式(3.1)、(3.2)の収束をより困難にします。さらに2つの接近したプレートの分離には、薄く低い粘度の領域を必要とします。このテスト問題では、こうした低粘度領域に数10キロメーターの幅を持たせ(全四角形領域サイズは数千キロメーター)、粘度は高温マントルと同程度に設定しました(それが冷たく硬い岩石圏に在るとしても)。この低粘度領域と周囲の岩石圏は急激な粘度変化を形成します。 |
| 4. | 「複雑3次元テスト問題」は「複雑2次元テスト問題」と同じ性質を多く持ちます。沈み込み帯は設定されますが、接触が停止された状態です(2つの大陸が衝突した状況ですが、それらは共に沈み込まないようにされます)。この場合には、既に沈み込んだ岩石圏はマントル内に垂直にハングアップし、最終的に外れたり、あるいは高温マントル内に拡散します。この設定は全て3次元モデル化されましたが(これはかなりの計算が必要です)、弱い非干渉領域は不要なため、収束性は向上すると期待されます。 |
3.5 結果
ここではセクション3.4で述べたテスト問題の結果を示します。各テスト問題は、先述のフェーズ2で可能になった4つのマルチグリッド法全てを用いて解かれました。MG法の実行時間は秒単位で示され、解法に用いたMPIプロセス数も示します。MG法の実行時間およびそのMPIプロセス数を、並列時のスケーリング性能を反映させるために、対数スケールで視覚的にプロットします。さらに詳しく評価するために、温度と速度場をチャートで表現します。このチャートは2Dテスト問題に対しては、温度と速度場をxz平面にプロットしたものです。同様に3Dテスト問題では、温度をxz平面とyz平面に、速度場をxy平面とxz平面にプロットしました。
2Dテスト問題では、2,4,8,16,32,64のMPIプロセス数に対して結果を得ました。HECToRのクアッドコア構成においては、ノード当たり4コアであることから、実行時に必要なメモリーに制限が生じました。HECToRにおいては利用可能なメモリーがノード当たり8GB、コア当たり2GBであるため、2Dテスト問題では2と4MPIプロセスの場合に、MPIプロセス当たりの問題サイズが大きくなってしまい、メモリーに収まり切れませんでした。このため、2MPIプロセスのジョブはノード当たり1コアのみを使用し、4MPIプロセスではノード当たり2コアのみを使用して実行しました。2Dテスト問題においては、他のジョブは全てノードを飽和して実行が可能でした。
同様に3Dテスト問題では、32,63,128,256MPIプロセスを用いて結果を得ました。ここでも32と64MPIプロセスは2Dテスト問題と同様にメモリーが十分でなかったため、32MPIプロセスのジョブはノード当たり1コアのみを使用し、64MPIプロセスではノード当たり2コアのみを使用して実行しました。3Dテスト問題の他のジョブは全てノードを飽和して実行が可能でした。
3.5.1 単純2次元テスト問題
単純2次元テスト問題における各MG法の100時間ステップの実行時間を、表3.1に示します。図3.4では、この数字をMPIプロセス数に対してプロットしました。これらの結果から、Vサイクルは、2から32のMPIプロセス数において他の方法と比べて性能が良いことが解ります。この他着目すべき点として、FMG(V)とWサイクルの性能は互いによく似ています。
| Number of Processes | Time(in seconds) | |||
| V-cycle | W-cycle | FMG(V) | FMG(W) | |
| 2 | 3902 | 4754 | 4487 | 5987 |
| 4 | 1851 | 2264 | 2104 | 2695 |
| 8 | 1026 | 1266 | 1177 | 1515 |
| 16 | 523 | 647 | 613 | 799 |
| 32 | 278 | 354 | 352 | 479 |
| 64 | 182 | 236 | 265 | 384 |
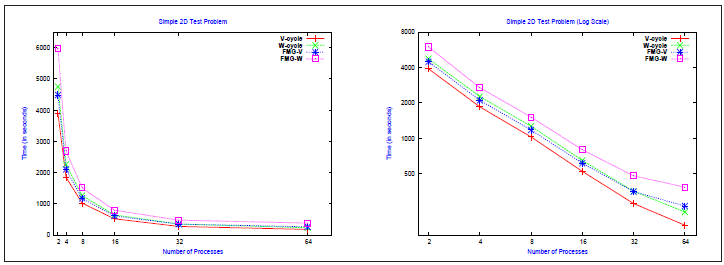
図3.4:単純2次元テスト問題のMG法の並列性能とスケール性
FMG(W)法は、他の手法に比べて多少コストが掛かりますが、傾向は似ています。この性能差はこのMG手法の性質に原因があります。さらに、図3.4の対数表示から、実行時間の小さな差異を除いて、全ての手法は32MPIプロセスまで同じ傾向で良好なスケール性が示されています。64MPIプロセスにおいて僅かな性能劣化が有りますが、これは各MPIプロセスにおけるサブ問題のサイズが小さすぎるためで、各方向についてMPIプロセス当り2要素しかないためですが、この場合は性能やスケール性としては十分許容範囲内です。
100ステップ計算後の温度と速度場を図3.5に示しました。ここでは2次元の問題のため、温度と速度場をXZ平面上に描画しました。
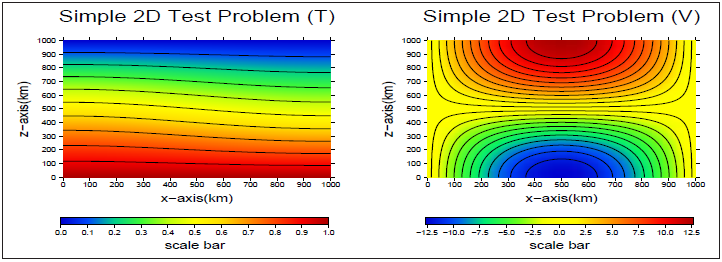
図3.5:単純2次元テスト問題の温度と速度場
3.5.2 単純3次元テスト問題
ここでは単純3次元テスト問題の結果を示します。以前にセクション3.3で説明しましたが、このテストは前セクションで扱った単純2次元テスト問題の拡張です。
計算は32から256MPIプロセスを用いて行いました。表3.2において、様々なMPIプロセス数に対して、各MG法が100ステップ実行に掛かる時間を示し、図3.6に図示しました。これらは、VサイクルとFMG(V)法が良く似た性能を持ち、予想通りWサイクルとFMG(W)法よりも僅かに勝っていることを示しています。
| Number of Processes | Time(in seconds) | |||
| V-cycle | W-cycle | FMG(V) | FMG(W) | |
| 32 | 21826 | 24656 | 21935 | 25907 |
| 44 | 13548 | 16354 | 13194 | 16736 |
| 128 | 5851 | 6674 | 5869 | 7039 |
| 256 | 3635 | 4420 | 3586 | 4641 |
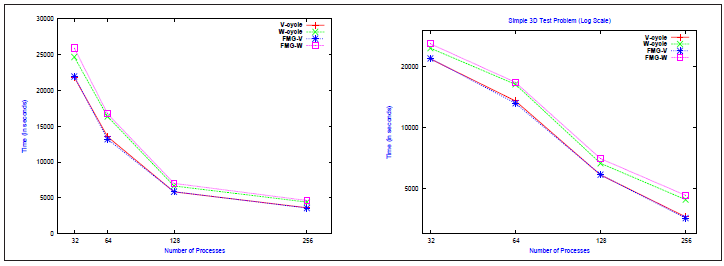
図3.6:単純3次元テスト問題のMG法の並列性能とスケール性
図3.6の対数グラフはこれをより明確に示しており、実行時間の僅かな差を除いて、全手法は同じ傾向を示し、32から256MPIプロセスまで良好なスケール性を示しています。このテストにおいてはプロセス当たりのサブ問題のサイズは十分大きく、スケール性の悪化は見られません。言い換えれば全てのMG手法はMPIプロセス数の増加に対して良好な性能を示し、MPIプロセス当たりのサブ問題サイズが減少しても、もはや2次元で見られたような小さすぎる状態にはなりません。ただし、ノード当たりのコア数の変化に伴ったグラフの折れ曲がりを見ることが出来ます。
100ステップ実行後の温度と速度場を図3.7に示します。今度は3次元のため、温度をyz平面とxz平面に、また速度場をxz平面およびxy平面に描画しました。この図は表面および表面から400と800キロメーターの位置での値を描いています。xy平面の速度場以外は差異はほどんどありません。
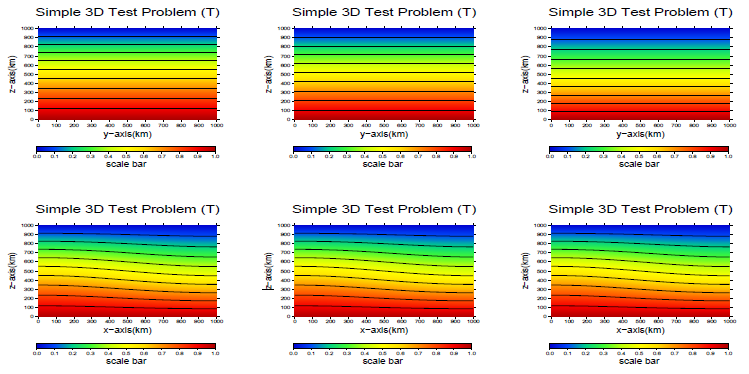
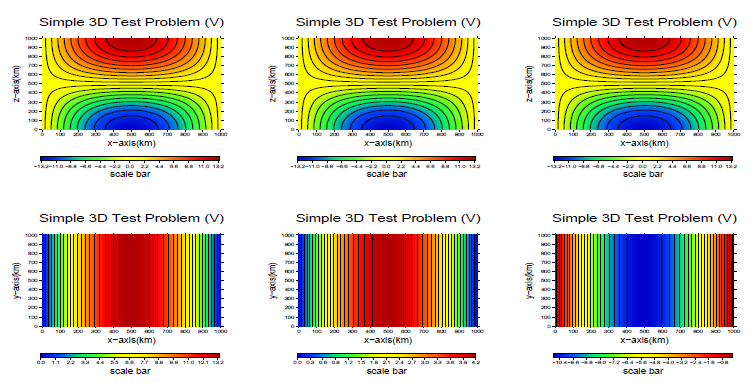
図3.7:単純3次元テスト問題の温度と速度場
3.5.3 複雑2次元テスト問題
この問題を数値的に解くのは極めて難しく、VサイクルとWサイクル法の弱点の認識に役立ちました。これらの手法はHECToR上のジョブの最大許容時間である12時間以内に収まりませんでした。一方、FMG(V)とFMG(W)法は4から64MPIプロセスを用いて収束しましたが、2MPIプロセスの場合は異常終了しました。
| Number of Processes | Time(in seconds) | |||
| V-cycle | W-cycle | FMG(V) | FMG(W) | |
| 2 | - | - | * | * |
| 4 | - | - | 22883 | 23238 |
| 8 | - | - | 14005 | 18396 |
| 16 | - | - | 8934 | 12493 |
| 32 | - | - | 5676 | 8286 |
| 64 | - | - | 5815 | 7600 |
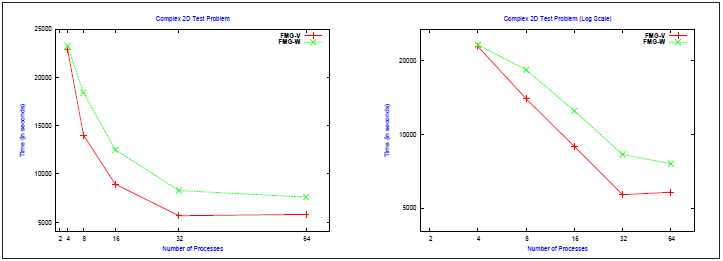
図3.8:複雑2次元テスト問題のMG法の並列性能とスケール性
FMG(V)とFMG法の100ステップ実行時間を表3.3、MPIプロセスに対するプロットを図3.8に示しました。8から64MPIプロセスにおいてはFMG(V)法がFMG(W)法に性能で勝ります。性能の傾向は共に、全体的には似ています。両者は特に4MPIプロセスではほとんど同じです。また、64MPIプロセスにおいて、MPIプロセス当たりの問題サイズの影響で、性能が劣化します。性能劣化はFMG(V)法の方が悪く、64MPIプロセスの値が32MPIプロセスでの時間を上まっています。この現象を除けば、両者の32MPIプロセスまでのスケール性は極めて良好です。
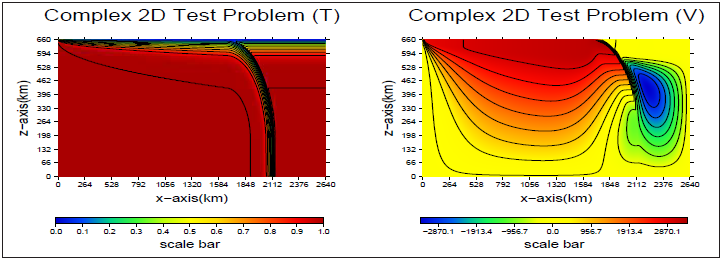
図3.9:複雑2次元テスト問題の温度と速度場
100ステップ実行後の温度と速度場を図3.9に示します。2次元問題のため、温度と速度場をxz平面に描画しました。この図は表面および表面から400と800キロメーターの位置での値を描いています。xy平面の速度場以外は差異はほどんどありません。この図はVサイクルとWサイクルの収束失敗を原因とする、相の急激な変化を示しています。
3.5.4 複雑3次元テスト問題
この問題を解くのは、単純3次元テスト問題に比べれば困難ですが、先ほどの複雑2次元テスト問題に比べれば容易です。この問題もMG法のまた別の局面を認識するのに役立ちました。
全てのMG法について100ステップの実行時間を表3.4に示します。Vサイクル法のみ、HECToRの12時間制限を超えてしまい、64MPIプロセスで88ステップを実行して中断されました(繰り返し実行を試みましたが88ステップまでしか実行でしませんでした。対照的に32MPIプロセスでは100ステップ実行が完了できており、この問題は解決していません)。
| Number of Processes | Time(in seconds) | |||
| V-cycle | W-cycle | FMG(V) | FMG(W) | |
| 32 | 42960 | 31386 | 26940 | 34940 |
| 64 | * | 21205 | 16305 | 22440 |
| 128 | 13167 | 8147 | 7166 | 9306 |
| 256 | 12031 | 5469 | 4423 | 6150 |
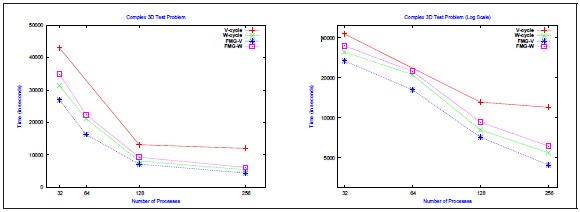
図3.10:複雑3次元テスト問題のMG法の並列性能とスケール性
図3.10にMPIプロセスに対する実行時間が示しました。32から256MPIプロセスでは、FMG(V)法が他の手法に比べ性能で勝り、次にWサイクル、FMG(W)、Vサイクルと続きます。Vサイクルが64MPIプロセスで100ステップ実行できなかったことと、256MPIプロセスで性能悪化することを除けば、他の手法は似た傾向を示しています。このスケール傾向は単純3次元テスト問題のものと似ています。
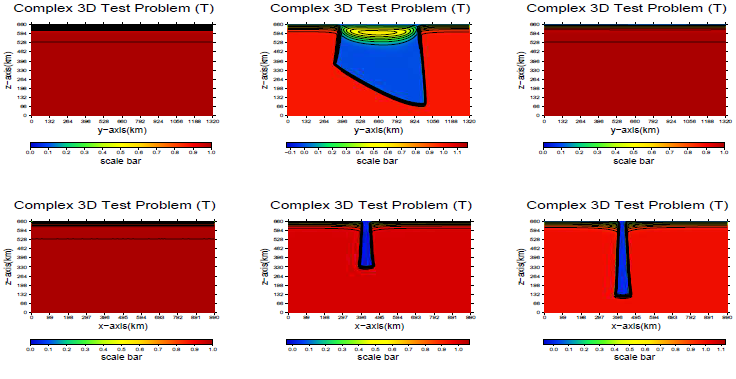

図3.11:複雑3次元テスト問題の温度と速度場
100ステップ実行後の温度と速度場を図3.11に示します。温度をyz平面とxz平面に、速度場をxz平面とxy平面に描画しました。この図は表面および表面から400と800キロメーターの位置での値を描き、そこでの温度と速度場の変化を表しています。
3.5.5 結果の纏め
これら4つの代表的なテスト問題の結果から導かれる点を以下に纏めます:
- CITCOMは単純2次元テスト問題において、VサイクルはFMG(V)に比べ31%高速、WサイクルはFMG(W)に比べて38%高速である。また複雑3次元テスト問題において、WサイクルはFMG(W)に比べて12%高速である。これらは最も速い場合の値から算出されている。
- Vサイクル法は、単純で収束が容易な問題に対しては、最も速い手法である。
- FMG法は、複雑な問題に対しては、VサイクルやWサイクルに比べて良好な性能を示す。またこの場合、後者は収束性が悪化する場合がある。
- Vサイクル系のMG法は、一般に、Wサイクル系のMG法より性能で勝る。
- 収束を制御するMG法のスケール性能は、一般に優れている。これは、MPIプロセスが受け持つサブ問題サイズが計算可能なサイズ、すなわち各方向におけるMPIプロセス当たり2要素、まで減らない場合に特に当てはまる。
- Vサイクル法が比較的簡単な問題に対する最適で、比較的複雑な問題に対してはFMG(V)が最適である。
- スケール性能は、ノードの全てのコアを用いる場合に比べて、ノード当たり1コアあるいは2コアを用いる場合にはより影響を受ける。
3.6 ポスト処理ツール
ここでは、本プロジェクトで用いたデータ処理ツール/ユーティリティを紹介します。
3.6.1 CITCOMツール
CITCOMのプスト処理ツールの概要と利用方法について記します。
3.6.1.1 combcoord
このプログラムは、各領域の局所座標情報を組み合わせて、最も細かいグリッドレベルにおける全てのノード点に対するグローバル座標を構築します。
利用シンタックス: combcoord <inputfile>
3.6.1.2 combany
このプログラムは、各領域に対応するファイル<basename>.temp. <procID>.<timestep>の一行目を組合せ、グローバルノード点に対応する温度場を構築します。これらのファイルの一行目には温度場関連データが含まれています。
利用シンタックス: combany <inputfile> temp <timestep>
3.6.1.3 combvel
このプログラムは、各領域に対応するファイル<basename>.temp. <procID>.<timestep>から速度場を抜き出し、グローバル速度場を構築し、それをグローバルノード点へ割当てます。これらのファイル内の、2,3,4列がそれぞれ速度場のx,y,z成分を示します。
利用シンタックス: combvel <inputfile> <timestep>
ツールcombcoord、combany、combvelは、同じ順序で座標、温度、速度場を格納します。こうしてグローバルノード点はこれらの値に正しく対応付けられます。コマンドラインのパラメーターは全ての場合について以下の意味を持ちます:
- inputfileはCITCOM実行の入力ファイルである。
- tempは、データファイル名に用いるノード点上の場の名前で、例えばtempは温度場である。
- timestepはCITCOMに出力させる時間間隔である。
3.6.1.4 reggrid
このプログラムは、combcoord、およびcombanyかcombvelのどちらか一つにより生成されたデータを読み込み、温度か速度場に関する全ての情報をデータ出力します。これはセクション3.5で示したチャート図を作成するのに利用できます。
利用シンタックス: reggrid <inputfile> <field> <snapshot> <orientation> <coordinate> <discretization> <discretization>
3.6.1.5 regvector
このプログラムはreggridと同等ですが、流れの向きを示す矢印を追加します。
利用シンタックス: reggrid <inputfile> <field> <snapshot> <orientation> <coordinate> <discretization> <vectorscaling>
ツールreggridとregvectorについては、コマンドラインパラメーターはほぼ同じです:
- inputfileはCITCOM実行の入力ファイルである。
- fieldは、データファイル名に用いるノード点上の場の名前で、例えばtempは温度場である。
- snapshotはtimestepと同じ。
- orientationは固定するx、y、z座標である。例えばyと指定すればxz平面描画を意味する。
- coordinateは固定するx、y、z座標の値である。2次元では,y 0のみ指定可能である。
- discretization: reggridは面内の2方向に別の離散化を許すが、regvectorは両方向に同じである。この値はキロメーター単位である。
- vectorscalingは無次元のスケーリングベクトルサイズである。値が小さければベクトルサイズも小さくなる。通常は0.001である。
3.6.2 Gnuplot
Gnuplot[13]はGLPライセンスのオープンソースソフトウェアで、ポータブルかつコマンドライン操作が可能な、UNIX,MS Windows,DOS等の多くのOS上でインタラクティブにデータや関数を描画する機能を持ちます。また2次元および3次元の様々な種類の描画タイプをサポートしています。線、点、ボックス、コンター、ベクトル場、サーフェース、および付随するテキストが表示できます。また様々な専門的なプロット種類もサポートされます。Gnuplotは様々な異なる種類の出力をサポートしています:インタラクティブな画面端末、プロッターや現代的なプリンターへのダイレクト出力、例えばeps, fig, jpeg, LaTeX, metafont, pbm, pdf, png, postscript, svg等。本レポートで示した図は全てGnuplotを用いて描画しました。
3.6.3 Generic Mapping Tools(GMT)
GMT[14]は60以上のプログラムを含むオープンソースソフト群で、フィルタリング、トレンドフィッティング、グリッディング、プロジェクション等、地理およびカルテシアン座標データを扱い、単純なxyプロットからコンター図や彩色表面、3次元投射に至る図面のポストスクリプトファイルを生成します。GMTは約30のマッププロジェクション、変換をサポートし、様々なデータ形式をサポートします。セクション3.5のチャート図は、下記表3.5のGMTコンポーネントを使って生成しました。
| プログラム | 説明 |
| grdcontour | 2次元グリッドデータの等高線作成 |
| grdimage | 2次元グリッドデータのイメージ作成 |
| makecpt | カラーパレットテーブル作成 |
| psbasemap | basemapプロット作成 |
| psscale | マップ上へグレースケールあるいはカラースケールをプロット |
| xyz2grd | 等間隔xyzテーブルファイルを2次元グリッドファイルへ変換 |
3.7 次期フェーズ作業の検討
次期フェーズ3は2つの作業を行います:
- 粘度勾配が高い場所でのメッシュ・リファインメント
- 延長補間と制限補間の改善
CITCOMコードの構造の中へこれらを組込む妥当性の検討を含めて、上記作業を概説します。
3.7.1 メッシュ・リファインメント
MG法で用いるメッシュ・リファインメントは、速度や粘度の勾配が大きな場所で通常用いられる、連続的な要素サイズの縮小とは明確に異なります。このような方法で、ネストしたMGメッシュを持つ構造メッシュと組み合わせるのは大変に困難です。MG法では、自然な形で局所メッシュ・リファインメント手法が導かれます。局所的に一つ以上の細かなレイヤーを付け加えることにより、局所的に2あるいは2のべき乗倍に解像度を上げることは可能です。均一な局所的リファインメントの例を、図3.12(左図)に示してあります。ここでは境界要素のみリファインしています。
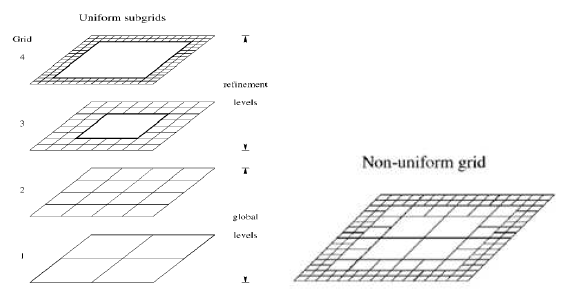
図3.12:均一(左図)と不均一(右図)なリファインメントの例
非均一な局所的リファインメントはより複雑で実装が難しいものです。これを図3.12(右図)で示します。より細かいMGレベルのグリッド要素は全体に存在しているわけではないため、特殊な取り扱いが要求され、解法が複雑になります。こうした複雑さを扱うには、さらに、内部境界上のゴーストノード点を持つレイヤーや、存在しないより細かいグリッドレベルの情報の記録機能を追加して用いる必要があります。こうしたことは大きなメモリーを要求し、ほとんどの場合に負荷分散を発生させます。
3.7.2 延長補間と制限補間の改善
延長補間と制限補間は、異なる平均化手法を適合させることにより[1]、収束性が改善する可能性があります。しかしながら、重み付き平均を基にした制限補間、および重み付き内挿補間を基にした延長補間という、現状の実装に対しては有効でないと判断しました。
4.リファインメント
この章では、本提案の2つのトピックを扱います:
- 延長補間と制限補間:これらは収束率改善へ寄与するか
- 局所メッシュ・リファインメント:例えば、高粘度勾配領域の部分メッシュリファインが収束率改善へ寄与するか
4.1 延長補間と制限補間
先ほどのセクションにおいて設定した2つの実装作業は、(i)局所メッシュ・リファインメントの実装および、(ii)算術平均、幾何平均、調和平均、および行列依存転送を用いた延長補間と制限補間演算の改善です。延長補間と制限補間の改善については、既存のコードに実装する前にそれがCITCOMに有益であるかどうか調べる必要があります。延長補間、制限補間操作は、マルチグリッド法において、下位レベルと上位レベルのノードの値からそれぞれ上位と下位のレベルに更新を掛けるものです。これらの演算に対して、異なる平均操作[1]を適用することにより、収束率は改善する可能性がありました。
結果として、延長補間(重み付き平均)と制限補間(重み付き内挿)の現状の実装に関して調査を行った結果、既存の実装においてこのような平均化手法を行っても利得は得られないとの結論に至りました。よって残りの作業期間は局所メッシュ・リファインメントに注力することとしました。
4.2 局所メッシュ・リファインメント
セクション3.7.1で述べた基本的なアイデアに従って、ここでは、以下に詳述するCITCOMに実装するグリッド適合方法の文脈における概念を拡張します。
4.2.1 リファインメント方法
言わばこの局所メッシュ・リファインメント手法は、ある条件に従って動的に選ばれた領域の一部/サブ領域の空間的解像度を増加させることと言えます。領域のどの部分を選択するかは決まったものではありませんが、一般的な説明として、リファインメント条件とリファインメント領域は予め知られていることを仮定していました。このリファインメント領域はz方向の断片であり、少なくとも2要素、あるいはレベル0メッシュで2要素以上が有る場合は偶数個の要素から成ります。負荷分散を回避して、岩石圏が位置する地表面近傍で生じる、速度のような鋭いグラジェントの多くを捕捉できるように、x方向とy方向の全ての要素をリファインします。レベル0において、領域表面近傍のメッシュに対しするこの局所メッシュ・リファインメントを一度行うと、このメッシュは2つの異なるサイズの要素から構成されることになります:(i)粗い要素、(ii)粗い要素に対して各方向に二分割され、2次元では4つの細かい要素となり、3次元では8つの細かい要素となり、メッシュ階層における高位のメッシュに対してリファインされたことになります。この点に関してはセクション2.2.1の議論が、CITCOMでカルテシアン座標がどのように使われるかを理解するのに役立つでしょう。
CITCOMには局所メッシュ・リファインメントが実装されていないため、CITCOMで用いる構造メッシュに対する局所メッシュ・リファインメントの実装について検討しました。結果として、負荷分散を引き起こさない領域表面の1レベルのみをリファインする、one-level-differenceリファインメント・ルールで実装することとしました。
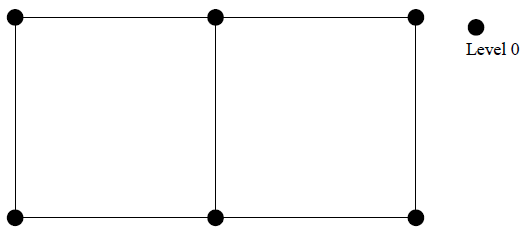
図4.1:レベル0の2次元メッシュにおける2要素
ここで局所メッシュ・リファインメントにおけるone-level-differenceリファインメント・ルールを詳しく述べます。ここで用いる局所メッシュ・リファインメントを説明するために、2次元における四角形および3次元における直方体のリファインメントをここで示します。図4.1は二次元における2つの要素を示しますが、これを使って、全メッシュ要素とノードがレベル0に存在する場合の局所メッシュ・リファインメントを説明します。
ここで、メッシュの右下隅およびその近傍においてこのメッシュを2レベルまでリファインすることとします。この時、レベル0の右下隅およびその近傍の要素はリファインメントの対象となり、この要素のリファインメントから得られた新しい要素はレベル1のメッシュを形成します。続いて、レベル1の右下隅およびその近傍の要素は、再度レベル2を形成する新しい要素へリファインされます。
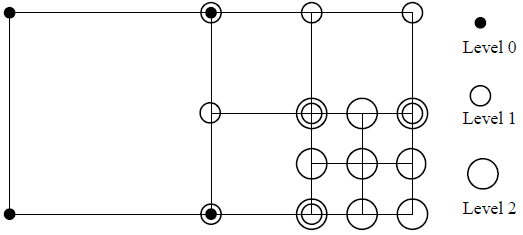
図4.2:one-level-differenceリファインメント・ルールを用いない場合の局所メッシュ・リファインメント
このやり方は図4.2で2次元要素として示されており、ここでリファインされたサブ要素は各方向のより粗いレベルの要素を二分割したものとなっています。この例ではx方向とy方向に対して、要素がリファインされる毎に4つの要素が生成されています。右下隅近傍の要素のリファインメント後に、全8つの要素が得られました:(i)レベル0の1要素、(ii)レベル1の3要素、(iii)レベル2の4要素。レベル0のノードは黒丸、小円はレベル1、大円はレベル2のノードに対応しています。異なるレベルの2つの要素を共有する如何なるノードも、黒丸と小円か、小円と大円のどちらかです。しかしながら、このリファインメント方法はone-level-differenceリファインメント・ルールに従うものではありません。
リファインメントの観点からは全く問題ありませんが、マルチグリッド法ではうまく行きません。これは異なるメッシュレベルを固定させており、さらにメッシュを高位のレベルへリファインさせるにつれてより困難になって行きます。よってこれはCITCOMに最も適した手法とは言えません。
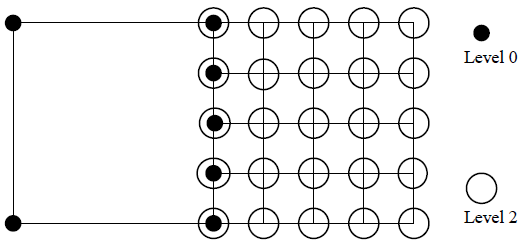
図4.3:one-level-differenceリファインメント・ルールで許されない局所メッシュ・リファインメント
右下隅およびその近傍の要素に対するリファインメントには別のやり方があり、それは図4.3に示すようなレベル2です。これはメッシュ内に2つの両極端の要素を生成します:(i)最も粗い要素および、(ii)粗いレベルの要素に比べて、2次元では4n倍小さい要素、3次元では8n倍小さい要素。ここでnはリファインメントの最高位レベルを示します。このリファインメントは、one-level-differenceリファインメント・ルールにより禁止されます。さらにこれは、粗い要素のエッジに多くのhanging nodeを生成することになり、これらhanging nodeの取り扱いに余分な仕事が増えるだけでなく扱いの複雑さを増してしまうことになります。
再度、メッシュの右下隅およびその近傍において2つの要素を2レベルまでリファインすることを考えます。ですが今度は、one-level-differenceリファインメント・ルールに従います。このルールは、リファイン処理後(この場合はレベル2まで)のメッシュにある全ての2要素は、リファインされたメッシュの階層の中で1違いのレベルにある事を要請します。言い換えれば、図4.4に示したように、レベル2までリファインされたときにはレベル0の要素は存在しません。このことは、リファインメント後の要素はメッシュ内の他の要素と最大1レベルの違いしかないことを意味します。よって右下隅およびその近傍の要素をレベル2までリファインすることは、他の要素は少なくとレベル1までリファインされていなければならないことを意味します。これは、[10]と[3]に記載されるone-level-differenceリファインメント・ルールに対して追加の制限を持ちます。これは、メッシュ内の全ての要素とノードがレベル1か2にある事を保証し、マルチグリッド法の延長補間と制限補間において、要素の多重レベル階層の取り扱い困難さを増やすことはありません。
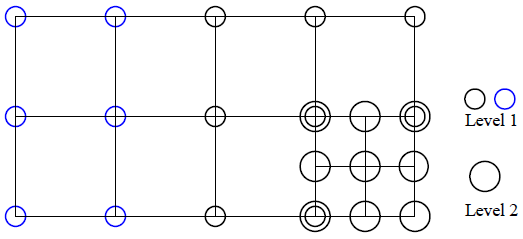
図4.4:one-level-differenceリファインメント・ルールによる局所メッシュ・リファインメント
ここで、図4.4で示したメッシュリファインメントのためには、右下隅およびその近傍の要素がレベル2までリファインされたならば、レベル0の全ての要素もリファインされていなければなりません。青円のノードを持つ要素はメッシュ内の他の要素がリファインメントされた結果としてリファインされた要素です。これは以下のように一般化されます:レベルnの要素がリファインされる際には、その結果全ての要素はレベルnかレベルn+1となるため、レベルn-1の要素はリファインされなければなりません。
ここまで記述したone-level-differenceリファインメント・ルールによる局所メッシュ・リファインメントから、CITCOMの現状の実装における幾つかの原理の制限を以下に述べます:
- 2次元および3次元において、z軸方向のメッシュのみがリファインされる。なお、CITCOMのカルテシアン座標は通常の(x,y,z)でなく(x,z,y)として定義される。
- リファインされたメッシュ部分は、リファインされない要素のレベルよりも1のみ高い。
- レベル0の局所メッシュ・リファインメント後、元のレベル0は粗い要素とされ、リファインメント後の新しい要素をレベル0と見做す。次の高位レベルへのリファインメントは、各レベルで同じメッシュ構造を維持するために、メッシュ全体を通して実行される。
- リファインされた要素との境界に当たる粗い要素エッジ上のノードは、リファイン済み要素かより高位のレベルの要素によってのみ扱うことが出来る。粗い要素にとってはそれは存在しないノードとして扱われる。
- 各メッシュレベルは2つのサイズの要素で構成される。つまり同一レベルにおいて粗い要素とリファインされた要素の2つがある。
- リファインされた要素と共有される粗い要素エッジ上のノード(少なくとも2以上)は、リファイン済み要素によってのみ扱うことが出来る。つまり全メッシュはhanging nodeを持たない。
4.2.2 リファインメント準備
セクション4.2.1のやり方に従って、ここでは2次元メッシュを用いて、CITCOMに実装された局所メッシュ・リファインメントを記述します。この説明に当たり、x軸方向に8要素、z軸方向に6要素の小さな2次元メッシュを用います。これは図4.5の黒線で示される4つのサブ領域から成ります。
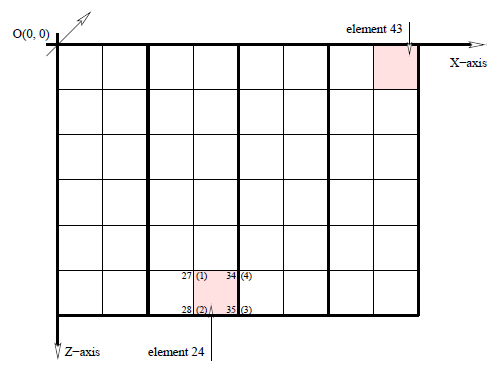
図4.5:2次元の48要素から成る粗いメッシュ
各サブ領域における問題を解くために、各サブ領域当り1プロセスを割当て、全体としては4プロセスを用います。x方向に4プロセス、z方向に1プロセス、つまり各プロセスはz方向全体を扱うこととします。ここで、CITCOMはz方向への複数プロセス割当てを許可していません。その副産物として、全プロセス負荷はバランスして、z方向の通信は発生しません。これはone-level-differenceリファインメント・ルールを選んだ理由の一つでもあります。要素番号24の結合情報は、局所ノード番号1,2,3,4に対してそれぞれ、ノード番号27,28,35,34によって与えられます。メッシュ内の要素番号付けは、原点(0,0)隣の1から始まり、z軸に沿って番号付けられ、次にx軸を一つ移動して繰り返されます。同様にグローバル番号は同じパターンを用います。ただし局所ノード番号は反時計回りです。これは図4.6に示す3次元における、3番目のy軸へ拡張されます。説明の便宜上さらに小さなサイズのメッシュを示しています。
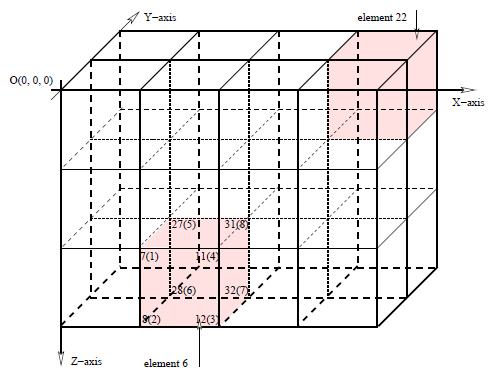
図4.6:3次元の24要素から成る粗いメッシュ
one-level-differenceリファインメント・ルールとセクション4.2.1で述べた条件から、図4.5のメッシュは、z方向の上部から2要素、z方向に8要素、およびy方向に2要素を含む部分がリファインされます。この局所リファインメントは、既存の要素を全方向について半分のサイズで倍の数の要素に置き換えます。言い換えれば、2次元では図4.7で示すように、元の要素の1/4の大きさのより小さな要素4つで置き換えられ、3次元では図4.8で示すように1/8の大きさのより小さな要素8つで置き換えられます。
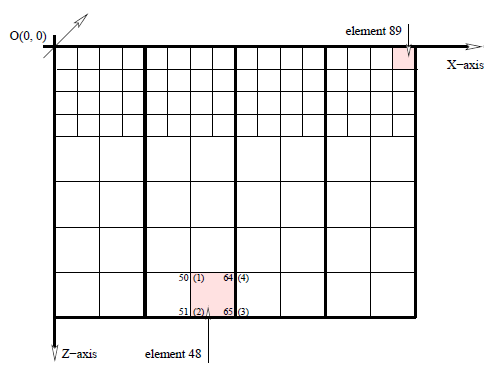
図4.7:2次元の領域上部の粗いメッシュの局所リファインメント
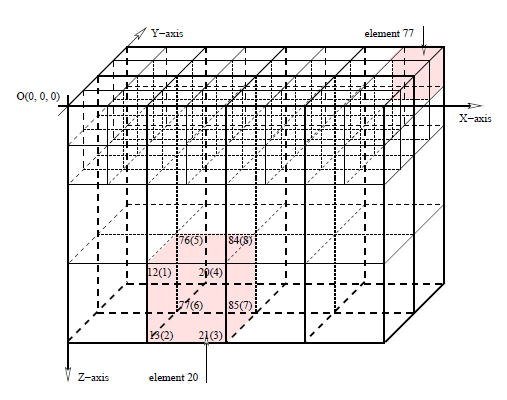
図4.8:3次元の領域上部の粗いメッシュの局所リファインメント
ここで重要なのは、これら新しい要素がベースレベルあるいはレベル0に在る親要素と同じレベルにある事です。このベースレベルメッシュの準備後に局所リファインメントを行い、メッシュ内の全要素をリファインして次のレベルが得られます。よってあるメッシュレベルにおける領域上部の要素は、常にそのレベルのメッシュ内の他の要素よりは小さくなりますが、全要素は同じレベルにあります。
ベースレベルのメッシュのリファインメント領域を指定するために、CITCOM入力ファイル内で閉領域を指定します。これは2つあるいは3つのペアの値、即ち2次元および3次元に対し、(xmin,xmax)、(zmin, zmax)、(ymin,ymax)で指定されます。これらの値を入力ファイルで指定して、実行時にメッシュ・リファインメント領域を制御します。これにより、全ソースコードをリコンパイルせずに、柔軟なリファインメント領域の実験が可能です。
CITCOM内への局所メッシュ・リファインメントの実装は、多数の関数の大きな書き換えが必要とされます。それは特にCITCOMで定義されたC言語構造体に関するもので、要素、サブ要素、ノード、表面ノード、隣接ノード、ノードマップ、座標、領域分割、隣接サブ領域、通信ルート、境界条件、延長補間と制限補間の準備等の機能と構築を提供しています。これらの構造、準備、これら構造体メンバーへのアクセス方法、コードの変更に関する概要を、次のセクションで記述します。
4.2.3 リファインメント実装
ここでは、CITCOM内の62の構造体の内2つのスナップショットを用いて、ソースコードの構造体へ反映させることを考えましょう。この他にも大量にマクロやルックアップ・テーブルがあり、これらは計算に用いる構造体や配列の構築と代入に利用されています。例えば、IEN structへメッシュレベルのグローバルノード番号と要素の局所ノード番号を登録し、これを用いて、NEI structへ与えられたノードが属する要素数とメッシュレベル等を登録します。こうした構造の一つがAll_variablesであり、他の変数と共に多くの構造体がネストされています。それら構造体のサイズは数個から膨大な変数まで様々です。これらの内struct Parallelは16行で出来ており、数個の変数と他の構造体をメンバーとして含むものです。これら構造体は数個から膨大な量のメンバー変数を含むものまで様々です。
局所メッシュ・リファインメント実装前の、メッシュ内での(グローバル)ノード番号を計算するコードのスナップショットを以下に示します。極めて単純なやり方で、y方向のノード数noyのループの後に、x方向のノード数noxのループ、最後にz方向のノード数nozのループという、よくある普通のループです。この最内側で、(グローバル)ノード番号が、スナップショットの4行目の式で決定されます。2次元の場合はもっと簡単になり、y方向のループと右辺第一項を無視出来ます。2次元の図4.5と3次元の図4.6を見れば、ノード番号の計算はそれほど難しくはありません。
局所メッシュ・リファインメント実装前のグローバルノードの決定方法 for (ky=1; ky <= noy; ky++) { for (ix=1; ix <= nox; ix++) { for (jz=1; jz <= noz; jz++) { node = (ky-1)*nox*noz + (ix-1)*noz + jz; }/* end of for jz=1 */ }/* end of for ix=1 */ }/* end of for ky=1 */
局所メッシュ・リファインメントの場合も同様です。y,x,z方向に対してnoy,nox,nozのループも同じです。しかしながら、メッシュのリファインされている部分と粗い部分の区別が必要になります。このために以下の変数を追加しました:
- znmax:z方向の最大ノード数
- znbnd:z方向のメッシュのリファインされた部分(band)に在るノード数
- zxnd1:メッシュのリファインされた部分と粗い部分を覆うzx平面内に在るノード数
- znbnd:メッシュのリファインされた部分のみを覆うzx平面内に在るノード数
以下のスナップショットで、ynodes,xnodes,xnalt,znaltはローカル変数です。各ループ内の増分は、ループカウンタが奇数、偶数、またはその組み合わせに依存します。
局所メッシュ・リファインメント実装後のグローバルノードの決定方法 int znmax = E->info.znmax; int znbnd = E->info.znbnd; int zxnd1 = E->info.zxnd1; int zxnd2 = E->info.zxnd2; ynodes = 0; for (ky=1; ky <= noy; ky++) { ( 1==(ky%2) ) ? (xnalt=zxnd1) : (xnalt=zxnd2); xnodes = 0; for (ix=1; ix <= nox; ix++) { if ( ky%2 ) { 11 ( 1==(ix%2) ) ? (znalt=znmax) : (znalt=znbnd); } else { znalt = znbnd; } for (jz=1; jz <= znalt; jz++) { node = ynodes + xnodes + jz; }/* end of for jz=1 */ xnodes += znalt; }/* end of for ix=1 */ ynodes += xnalt; }/* end of for ky=1 */
ここで、局所メッシュ・リファインメント実装前後の、与えられた要素のサブ要素とメッシュレベルを決めるstruct ELのセットアップコードにおける差を比較してみましょう。元のコードでは、y,x,z方向の要素数ely,elx,elzのネストしたループが有ります。そのコードのスナップショットは以下のものです。各親要素は各方向に2つのサブ要素を持ち、2次元では4要素、3次元では8要素となります。先の(グローバル)ノード番号計算と同様に、要素番号と最初のサブ要素番号を決定します(z方向ループ直後の2行)。この番号と残りのサブ要素番号は、事前に定義されたルックアップテーブルとサブ要素数ループによりstruct ELへ登録されます。この手順は最高位レベル以外の全てのレベルに対して繰り返され、こうしてすべてが完了すれば、すべての要素のサブ要素に最高位レベルを除いて如何なるレベルでもアクセスできるようになります。
局所メッシュ・リファインメント実装前のstruct ELのセットアップ for (lev=E->mesh.levmax-1; lev >= E->mesh.levmin; lev--) { elx = E->lmesh.ELX[lev]; elz = E->lmesh.ELZ[lev]; ely = E->lmesh.ELY[lev]; elxu = 2*elx; elzu = 2*elz; for (ye=1; ye <= ely; ye++) { for (xe=1; xe <= elx; xe++) { for (ze=1; ze <= elz; ze++) { element = (ye-1)*elz*elx + (xe-1)*elz + ze; sub_element = 2*(ye-1)*elzu*elxu + 2*(xe-1)*elzu + (2*ze - 1); for (el=1; el <= ENODES[E->mesh.nsd]; el++) { E->EL[lev][element].sub[el] = ( sub_element + offset[el].vector[z] + offset[el].vector[x]*elzu + offset[el].vector[y]*elzu*elxu ); }/* end of for el=1 */ } /* end of for ye=1 */ } /* end of for ze=1 */ } /* end of for xe=1 */ }/* end of lev= ... */
局所メッシュ・リファインメント実装後のstruct ELへのサブ要素登録手続きは、これほど簡単ではありません。関連するコードのスナップショットを以下に示します。
局所メッシュ・リファインメント実装のstruct ELのセットアップ for (lev=E->mesh.levmax-1; lev >= E->mesh.levmin; lev--) { xemin = E->info.ELXP[lev]; zemin = E->info.ELZP[lev]; yemin = E->info.ELYP[lev]; xebnd = E->info.XEBND[lev]; zebnd = E->info.ZEBND[lev]; next = lev+1; xeminN = E->info.ELXP[next]; zeminN = E->info.ELZP[next]; yeminN = E->info.ELYP[next]; xebndN = E->info.XEBND[next]; zebndN = E->info.ZEBND[next]; for (ye=1; ye <= yemin; ye++) { for (xe=1; xe <= xemin; xe++) { for (ze=1; ze <= zemin; ze++) { element = (ye-1)*zemin*xemin + (xe-1)*zemin + ze; /* for refined element corresponding to base mesh */ if ( is_element_refined(E, lev, element) ) { sub_element = 2*(ye-1)*zeminN*xeminN + 2*(xe-1)*zeminN + (2*ze-1); for (elm=1; elm <= ends; elm++) { element_count = ( element + (ye-1)*(zebnd/2)*(xebnd/2)*(ends-1) + (xe-1)*(zebnd/2)*(ends-1) + (ze-1) + offset[elm].vector[z] + offset[elm].vector[x]*zebnd + offset[elm].vector[y]*zebnd*xebnd/xemin ); sub_element_count = ( sub_element + offset[elm].vector[z] + offset[elm].vector[x]*zeminN + offset[elm].vector[y]*zeminN*xeminN ); for (yeN=1; yeN <= yeminN; yeN++) { for (xeN=1; xeN <= xeminN; xeN++) { for (zeN=1; zeN <= zeminN; zeN++) { nxt_element_count = (yeN-1)*zeminN*xeminN + (xeN-1)*zeminN + zeN; if ( nxt_element_count == sub_element_count ) { for (el=1; el <= ends; el++) { E->EL[lev][element_count].sub[el] = ( sub_element_count + (yeN-1)*(zebndN/2)*(xebndN/2)*(ends-1) + (xeN-1)*(zebndN/2)*(ends-1) + (zeN-1) + offset[el].vector[z] + offset[el].vector[x]*zebndN + offset[el].vector[y]*zebndN*xebndN/xeminN ); }/* end of for el=1 */ }/* end of if nxt_element_count */ }/* end of for zeN=1 */ }/* end of for xeN=1 */ }/* end of for yeN=1 */ }/* end of for elm=1 */ }/* end of if ... */ /* for coarse element corresponding to base mesh */ else { element_count = ( element + (ye-1)*(zebnd/2)*(xebnd/2)*(ends-1) + (xe-1)*(zebnd/2)*(ends-1) + (zebnd/2)*(ends-1) ); for (el=1; el <= ends; el++) { sub_element_count = ( sub_element + offset[el].vector[z] + offset[el].vector[x]*zeminN + offset[el].vector[y]*zeminN*xeminN ); for (yeN=1; yeN <= yeminN; yeN++) { for (xeN=1; xeN <= xeminN; xeN++) { for (zeN=1; zeN <= zeminN; zeN++) { nxt_element_count = (yeN-1)*zeminN*xeminN + (xeN-1)*zeminN + zeN; if ( nxt_element_count == sub_element_count ) { E->EL[lev][element_count].sub[el] = ( sub_element_count + (yeN-1)*(zebndN/2)*(xebndN/2)*(ends-1) + (xeN-1)*(zebndN/2)*(ends-1) + (zebndN/2)*(ends-1) ); }/* end of if nxt_element_count */ }/* end of for zeN=1 */ }/* end of for xeN=1 */ }/* end of for yeN=1 */ }/* end of for el=1 */ }/* end of else */ }/* end of for ze=1 */ }/* end of for xe=1 */ }/* end of for ye=1 */ }/* end of for lev= ... */
ここで、以前と同様に、y,x,z方向の要素数ely,elx,elzのネストしたループを用いています。要素番号はコードの赤太字行(24行目)の単純な計算で決定します。2次元の場合はelyのループは無効になります。この要素番号はリファインする前のメッシュに対して決定されます。ここで、それぞれの要素は、メッシュの粗い部分かあるいは細かい部分に属しているかによって区別して、適宜扱う必要があります。これは簡単なユーティリティー関数を使って決めることが出来ます。もしある要素がメッシュの細かい部分に属していれば、実際にリファインされたメッシュを形成するリファインされた要素、つまりサブ要素が計算されます。こうしたリファインされた要素は、メッシュの粗い部分に属する要素と同じレベルのものです。
先に進む前に、struct ELを構成するのに用いる変数を定義します。
- (xemin, zemin, yemin):それぞれx,y,z方向のリファインメント前の現状のメッシュレベルでの要素数
- (xebnd, zebnd):それぞれx、z方向のリファインされたメッシュ部分(band)の現状のメッシュレベルでの要素数
- (xeminN, zeminN, yeminN):それぞれx,y,z方向のリファインメント前の次の高位メッシュレベルでの要素数
- (xebndN, zebndN):それぞれx、z方向のリファインされたメッシュ部分(band)の次の高位メッシュレベルでの要素数
現状のメッシュレベルで定義された変数は、メッシュの粗い部分と細かい部分における要素数を決定し、次の高位メッシュレベルで定義された変数は、現状のメッシュレベルがメッシュ階層の最高位に達するまで、現状のメッシュレベルでの各要素に対応するサブ要素を決定します。
このスナップショットにおいて、赤字行(24から60行)と青字行(65から90行)はそれぞれ、メッシュの粗い部分と細かい部分に在る要素のサブ要素が如何に決定されるか、および事前に定義されたルックアップテーブルとサブ要素のループを用いて如何にstruct ELへ登録されるかを示しています。この手順は、最高位レベルの一つ手前で開始され、下位レベルに向かって全メッシュレベルで全要素に対して繰り返されます。この操作が完了すれば、struct ELのセットアップは完了し、最高位レベル以外のメッシュレベルにおける要素のサブ要素へのアクセスが可能となります。
また、局所メッシュ・リファインメント実装のために、マイナーな変更がされたものを除けば、39個の関数が修正され、13個の関数を新規に追加開発しました。
4.2.4 結果
CITCOMの現状の枠組みの中では、局所メッシュ・リファインメントを実行するのは極めて困難です。CITCOMで用いられている有限要素は、2次元では四角形、3次元では直方体の構造要素です。各要素は2次元では4つのサブ要素、3次元では8つのサブ要素を持ちます。1つ以上の要素に対する局所メッシュ・リファインメントは、リファインされない隣接要素のエッジ上にhanging nodeを常に生じさせます。3次元の場合、hanging nodeはリファインされない隣接要素の表面上に生じます。リファインされない隣接要素のhanging nodeを持つ要素エッジ/表面の数は、リファインされた隣接要素の数に依存します。
これに対して本プロジェクトは、セクション4.2.1で述べたone-level-differenceリファインメント・ルールを用いました。二次元における構造グリッドのリファインメント実装は複雑ですが、その度合いは3次元で特に大きく、かつCITCOMコードの複雑な構造も伴い、この実装は簡単な作業ではありませんでした。しかしながらこうした困難な状況下で部分的ですが達成されました。
CITCOMでは、多くのループや繰り返しが存在し、これらループ内でCITCOMは与えられた問題に対し、速度場、温度場、圧力場、トレーサーなどを解きます。一つのループによる計算は、他のループの計算へ影響を与える可能性があります。言い換えれば、マルチグリッド法を実装したCITCOMのある部分は、与えられた問題に対して速度場のみを解きますが、コードの他の場所で行われた計算へも影響を与えることが有ります。
CITCOMは時間依存問題を解きますが、0時間ステップを計算するオプションもあります。この動作は入力ファイルで指定されます。CITCOMは0時間ステップに制限して、幾つかの小規模テスト(フェーズ2の小規模テスト)を実行できました。これを実行して見ましたが、局所メッシュ・リファインメントに思ったより長い時間が掛かりました。この原因は、局所メッシュ・リファインメントの結果、2つの異なるサイズの要素が滑らかに接続されずに互いに向き合っているためです。時間依存問題の場合は、計算は数回の時間ステップの後に悪化し始めます。個の振る舞いはまだ解明されていませんが、移流拡散関連の計算がその要因であるかもしれません。一方、移流拡散計算や局所メッシュ・リファインメントのために調整すべき修正が必要なトレーサー関連計算といった、コードのマルチグリッド法以外の部分が原因の可能性もあります。
5. 結論
本章では、CITCOMのマルチグリッド法による改善に関して行った作業結果を纏めます。セクション5.1で3つの作業フェーズの内容を述べ、セクション5.2で結果について簡単に纏めます。本章には今後の改善に関する事柄も含まれます。
5.1 作業サマリー
1章の本プロジェクトでは、作業計画とCITCOMパッケージの概要を纏め、2章においてCITCOMの理解を進めるための導入的な議論を行いました。3章では、マルチグリッド法、モデル問題、テスト問題、2,3次元の差代表的なテスト問題に対する結果とその解析を論じました。これらの結果は、4種のマルチグリッド手法を用いたもので、その各マルチグリッド法に対して良好なスケール性を示しました。続いて結果の表示などに用いるポスト処理ツールを示しました。4章では、局所メッシュ・リファインメントの方法、準備、実装およびその結果を説明しました。
5.2 結果
本プロジェクトによりCITCOMの収束性が向上しました。CITCOMは、ベストケースでは、単純2次元問題に対して、FMG(V),FMG(W)法と比較して、それぞれVサイクルマルチグリッド法により31%以上、Wサイクルマルチグリッド法により38%以上高速でした。同じくベストケースで、複雑3次元問題に対しては、FMG(W)法と比較してWサイクル法が12%以上高速でした。
3章で解析された4つのマルチグリッド法に関するその他の結果を以下に纏めます。
- Vサイクル法は、単純で収束が容易な問題に対しては、最も速い手法である。
- FMG法は、複雑な問題に対しては、VサイクルやWサイクルに比べて良好な性能を示す。またこの場合、後者は収束性が悪化する場合がある。
- Vサイクル系のMG法は、一般に、Wサイクル系のMG法より性能で勝る。
- Vサイクル法が比較的簡単な問題に対する最適で、比較的複雑な問題に対してはFMG(V)が最適である。
- 収束を制御するMG法のスケール性能は、一般に優れている。これは、MPIプロセスが受け持つサブ問題サイズが計算可能なサイズ、すなわち各方向におけるMPIプロセス当たり2要素、まで減らない場合に特に当てはまる。
- スケール性能は、ノードの全てのコアを用いる場合に比べて、ノード当たり1コアあるいは2コアを用いる場合にはより影響を受ける。よってノードを飽和して用いる場合が最もスケール性能が良い。これはマルチコア構成の有効活用という面からも支持される。
局所メッシュ・リファインメント実装は部分的ですが達成されました。CITCOMを、0時間ステップに制限して、幾つかの小規模テスト(フェーズ2の小規模テスト)を実行できましたが、局所メッシュ・リファインメントに思ったより長い時間が掛かっています。この振る舞いはまだ解明されていませんが、移流拡散関連の計算がその要因であるかもしれません。
5.3 今後の改善
CITCOMは以下のような将来的な改善の余地が多くあります。
- 移流拡散や対流関連の問題での温度場計算の文脈への局所メッシュ・リファインメントの適用。
- トレーサーに対する、局所メッシュ・リファインメントによるノードと要素数の変化の適用
- 大規模問題ではCITCOMは、HECToRの最大ジョブ実行時間(12h)を超えることが考えられる。 現状のオプションは、リスタート機能を用いる事である。しかしながら場合により、リスタート後の重複する計算が全実行時間の1/3を占める場合がある。これをリスタート計算用に出力させることが出来れば、重複計算は不要となり、各リスタート計算開始毎の同じ計算による時間の浪費を防ぐことが出来る。
文献
| [1] | Auth, C. and Harder, H. Multigrid solution of convection problems with strongly variable viscosity. Geophysical Journal International, 137:793-804, 1999. |
| [2] | Blankenbach, B. and et. al. A benchmark comparison for mantle convection codes. Geophysical Journal International, 98:23-38, 1989. |
| [3] | Boyer, Franck, Lapuerta, Cline, Minjeaud, Sbastian, and Piar, Bruno. A local adaptive refinement method with multigrid preconditioning illustrated by multiphase flows simulations. volume 27, pages 15-53. INRIA a CCSD electronic archive server based on P.A.O.L [http://hal.inria.fr/oai/oai.php] (France), 2009. published on-line. |
| [4] | Briggs,W., Henson, V., and McCormick, S. A Multigrid Tutorial. SIAM, 2000. |
| [5] | CitcomS: A finite element code for thermal convection problems relevant to earths mantle. http://www.geodynamics.org/cig/software/packages/mc/citcoms/. |
| [6] | Devillard, N. and Chudnovsky, V. Run-time function call tree with gcc. http://ndevilla.free.fr/etrace, March 8 2004. |
| [7] | Dikov, V. Multigrid methods for solving differential equations. Technical report, Ferien Akademie, September 2005. |
| [8] | Doxygen: Source code documentation generator tool. http://www.doxygen.org/. |
| [9] | HECToR: UK national supercomputing service. http://www.hector.ac.uk/. |
| [10] | Krysl, P., Grinspun, E., and Schröder, P. Natural hierarchical refinement for finite element methods. Internat. J. Numer. Methods Engrg., 56(8):1109-1124, 2003. |
| [11] | Moresi, L. and Gurnis, M. Constraints on the literal strength of slabs from three-dimensional dynamic flow models. Earth Plan. Sci. Let., 138:15-28, 1996. |
| [12] | Moresi, L. and Solomatov, V. S. Numerical investigation of 2d convection with extremely large viscosity variations. Phys. Fluids, 7(9):2154-2162, 1995. |
| [13] | Gnuplot. http://www.gnuplot.info/. |
| [14] | Wessel, P. and Smith, W. H. F. The generic mapping tools (gmt). http://gmt.soest.hawaii.edu/. |
| [15] | Zhong, S., Zuber, M. T., Moresi, L. N., and Gurnis, M. The role of temperature dependent viscosity and surface plates in spherical shell models of mantle convection. Journal of Geophysical Research, 105(B5):11063-11082, 2000. |
