プログラムの高速化・並列化サービスの事例

概要

CRYSTALは非経験的な電子構造および物性計算コードであり、その計算において、電子密度は、局所的ガウス型原子軌道から構築されるブロッホ関数の線形結合で表されます。本dCSEプロジェクトは、電子構造計算に対して、系のサイズにリニアな新しいアルゴリズム：分割統治(divide and conquer)法を導入します。本レポートは、このアルゴリズムを概説し、弱く結合する系に対して従来のCRYSTALと同じ結果を生成することを示します。

目次

1.イントロダクション

1.1 材料モデリングコードCRYSTAL

1.2 DFTの線形スケール性

1.3 プロジェクトのマイルストーン

2.分割統治法アルゴリズム

3.原理証明の例題

3.1 液体ネオン

4.性能試験

5.その他の有用な結果

5.1 タスク並列

5.2 密度行列の初期値の改良

6.制限

7.結論

1.イントロダクション

1.1 材料モデリングコードCRYSTAL

材料モデリングコードCRYSTAL[1-3]は、STFC(英国科学技術施設協議会、Science and Technology Facilities Council)・計算科学技術部門およびトリノ大学・理論化学グループにより開発されました。その機能は、物質の電子構造の非経験的な計算、およびその結果を用いた様々な物性計算です。CRYSTALで用いられる一電子波動関数は局所ガウス型関数の線形結合であり、1，2，3次元の周期/非周期系の電子構造の効率的な計算が可能です。これとは別の良く知られた方法に平面波基底がありますが、これは周期イメージ間に真空ギャップが必要となりますが、これは3次元空間内の非周期系の計算にとって無駄なものです。

局所基底を用いる最大の利点は、ハートレー・フォック(HF)法および、HF法の交換項を組み合わせたハイブリッド密度汎関数法(DFT)にとって比較的に便利であることです。このハイブリッド密度汎関数は、これまで多くの報告でHFや局所あるいは準局所的DFT法が十分に表すことのできなかった、物性のより正確なモデルとして広く用いられつつあります[4-6]。この他の利点として、全電子計算をルーチン的に計算できることがあります。ほぼ常に平面波基底で必要とされる、内核電子を表現する擬ポテンシャルは必要ではありません。

CRYSTALは、量子化学者や固体物理学者や物性研究者により、国際的に長期に渡って利用されています。それは特に英国の材料化学研究者にとって注目されています。CRYSTALの機能と性能の向上は継続的に行われています。対象となる系のサイズや複雑さが増す中で必要なことは、HECToRのようなHPC設備を最大限に有効活用できるようにCRYSTALを開発していくことです。

現在可能なCRYSTALの並列実行方法には、PCRYSTALと呼ばれるプログラムを用いたデータ複製手法と、I.J.Bush博士により開発されたMPP CRYSTALと呼ばれるプログラムを用いた($O(N^2)$以上を対象とした)分散データ手法[2]があります。分割統治法が最も適しているのは大規模系を対象とするため、データ複製手法は好ましくありません。よって本レポートの作業ではMPP CRYSTALを拡張することとします。

1.2&nbs;DFTの線形スケール性

物質の電子密度解析に対して最も広く用いられる自己無撞着な手法は、CRYSTALの標準的なアルゴリズムでもありますが、系のサイズの3乗に比例してスケールします(すなわち$O(N^3)$)。CRYSTALでは、大規模系に関して$O(N^3)$の演算を含むハミルトニアン(フォック行列あるいはコーン-シャム)の対角化がボトルネックとなります。ハミルトニアンの対角化以外の部分では、$O(N)$サイズの$N$個の状態を他の$N$個の状態と直交するように見つけなくてはならないので、2乗でスケールすることになります。こうした好ましくないスケール特性から、これまでの伝統的なDFT計算は数千原子が限界でした。一般に数百原子以上の計算は極めて稀です。

大規模系の計算のためにはオーダー$O(N^3)$をより低くすることが必要です。幸いにも、(密度汎関数法における)多電子系の電子間相互作用は多くの場合に短距離力として扱うことが出来て、密度行列は距離に関して指数関数的に減少します[7]。こうした電子のnear-sightednessを利用する様々な手法が、ONETEP[8]、CONQUEST[9]、SIESTA[10]等においてコード開発されています。本プロジェクトでは、セクション2で記述される分割統治法を採用しています。

1.3&nbs;プロジェクトのマイルストーン

本プロジェクトの目的はCRYSTALのコード内に、$O(N)$の分割統治法を実装することです。このアルゴリズム詳細はセクション2で述べます。本プロジェクトの主なマイルストーンは以下のものです：

1.	MPP CRYSTALのタスクファーミング動作検証
2.	系をサブシステムへ自動分割し、そのサブシステムを、タスクファーミングされたMPP CRYSTALインスタンス内で独立に動作させる
3.	全フェルミエネルギーと全密度行列計算のための、固有値及び固有ベクトルの通信を実装する。
4.	密度行列を多重局展開し、サブシステムを埋め込み、長距離静電効果を入れる。

本プロジェクトは当初2人年と見積もられましたが、最終的には15人月が掛かりました。

2.分割統治法アルゴリズム

分割統治法アルゴリズム(D&C)は比較的古いアイデアであり[11]、通信より計算に多くのリソースを持つ現代的なHPCマシンに適したものです。この手法は図1に示すように、電子のnear-sightedness性を利用して系をコア領域とハロ領域から成るサブシステムへ分割するという、概念的には比較的単純なやり方です。

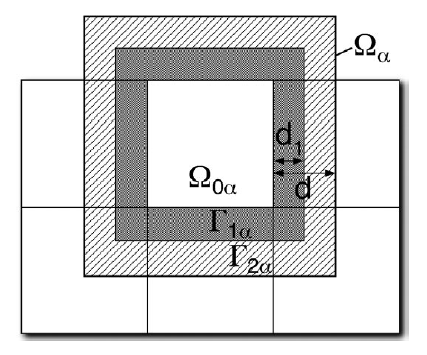
図1：系はサブシステム${\alpha}$に分けられ、各サブシステムはコア領域$\Omega_{0 \alpha}$、ハロ領域$\Gamma_{2 \alpha}$、および任意のその部分領域$\Gamma_{1 \alpha}$から校正される。サブシステムの電子状態は独立に計算され、これらから全電子構造が計算される。この図は文献[12]から転載した。

サブシステムは互いに結合していないものとして、各サブシステムの電子状態はその中で独立して計算されます。その後、全系のフェルミエネルギーと全密度行列が計算されて、これらから系の全エネルギーはコア領域からの寄与を加算して容易に計算出来ます。ハロ領域の電子状態は最後に削除されるものです。ハロ領域は、コア領域の電子状態を出来る限り全系の状態に近いものにするためだけに存在します。

より形式的には、系$\Omega$の一配位のエネルギー計算において、一粒子波動関数は局所基底関数${i}$の線形結合として表現され、全系はサブシステムの集合${\alpha}$で近似されます。ここで以下のパーティション行列を定義します

\begin{eqnarray} \mathbf{P}_{ij}=\sum_{\alpha} \mathbf{P}_{ij}^{\alpha}=1. \tag{1} \end{eqnarray}

通常のDFTやHF法で各サブシステムの電子状態を決定した後、全フェルミエネルギーを決定して電子数$N_{el}$を導きます。非磁性系では全電子は対になっていて、下記のように表現できます、

\begin{eqnarray} N_{el}=\sum_{ij} \rho_{ij} \mathbf{S}_{ij} =\sum_{ij} \left( 2\sum_{\alpha} \mathbf{P}_{ij}^{\alpha} \sum_m f_{\beta}(\epsilon_F-\epsilon_m) \mathbf{C}_{im}^{\alpha} \mathbf{C}_{jm}^{\alpha \dagger} \right) \mathbf{S}_{ij}, \tag{2} \end{eqnarray}

ここで、$\rho_{ij}$は(全)密度行列、$\mathbf{S}_{ij}=\langle i|j \rangle$は重なり積分、$f_{\beta}$は電子の温度$\beta$におけるフェルミ関数、$\mathbf{C}_{im}$は系$\alpha$の固有関数の行列表現です。式(2)を満たすフェルミエネルギー$\epsilon_F$は繰り返し法で解かれます。フェルミエネルギーが解れば、系の密度行列はサブシステム${\alpha}$からの寄与の和を取ることにより計算できます、

\begin{eqnarray} \rho_{ij}= 2\sum_{\alpha} \mathbf{P}_{ij}^{\alpha} \sum_m f_{\beta}(\epsilon_F-\epsilon_m) \mathbf{C}_{im}^{\alpha} \mathbf{C}_{jm}^{\alpha \dagger}. \tag{3} \end{eqnarray}

電子状態のこの手法による計算精度は、系のサブシステムへの分割に依存して変化します。本プロジェクトでは、2つの分割手法を実装しました。最も単純かつ保守的な方法は、一つのコア原子を含むサブシステムに分けるやり方です。この方法はSIESTA[10]に実装されており、マリケン・ポピュレーション解析と同等です。この方法はコア原子の周囲を囲むハロの半径をパラメーターとして持ちます。ハロの適切なサイズは扱う物質に依りますが、CRYSTALでは入力ファイルで指定可能です。系のパーティション行列は以下のように定義されます：

\begin{eqnarray} \mathbf{P}_{ij}^{\alpha}= \begin{cases} 1, & if & i \in \Omega_{\alpha} \land j \in \Omega_{\alpha} \\ 0.5, & if & (i \in \Omega_{\alpha} \land j \ni \Omega_{\alpha}) \lor (i \ni \Omega_{\alpha} \land j \in \Omega_{\alpha}) \\ 0, & if & i \ni \Omega_{\alpha} \land j \ni \Omega_{\alpha} \end{cases} \tag{4} \end{eqnarray}

ここで、$\Omega_{\alpha}$はコア原子に中心を置く基底関数の集合です。この極めて簡潔な系の分割はそれほど効果がありませんが、各サブシステムのコア領域に複数の原子を置くようにすると性能は改善できます。しかしながら、サブシステムに複数のコア原子が存在すると、ポテンシャルエネルギー局面に不連続点が存在する可能性が高まります[10]。サブシステムに一つの原子を持たせるのが最も安全な選択です。

もう一つ別の、本プロジェクトによる実装がユーザーにより明確に指定をする方法で、ユーザーは各サブシステムに対して具体的な原子(あるいはゴースト原子)を指定し、原子対のパーティション行列を手動で定義します。この方法においては、$\mathbf{P}_{ij}^{\alpha}$は、同じ原子上の全ての局所基底関数に対して同じでなくてはならないように実装されました。こうすることにより、D&Cアルゴリズムの使用に対する柔軟性がもたらされます。このように設計された系をサブシステムへ分割するコードは、コードの構造を変更することなしにパーティション行列を定義する新たな経験則を追加可能にしています。新たに実装されたD&Cアルゴリズムが必要とするのは、サブシステムの原子とそれから再構築された全系の原子とのマッピング配列と各サブシステムのパーティション行列のみです。

時間の関係上4番目のマイルストーンは完成しませんでした。系の長距離静電力は無視されていますが、極性の無い系にとってこれは差異を生じるものでなく、次のセクションで示すように静電力はハロを介したコア間の相互作用にほぼ含まれています。

3.原理証明の例題

3.1 液体ネオン

最初にD&Cアルゴリズムが密度行列に対して適切な近似ある事を示すために、単純なテストケースを使用します。D&Cアルゴリズムは弱く相互作用する系に対して最も適しています。CRYSTALの実装には長距離クーロン相互作用は含まれておらず、周期的な共有結合系ではサブシステムの電子状態に不都合が生じます(セクション6を参照してください)。古典分子動力学シミュレーションで用いられていた10Å ³の立方体に閉じ込められたネオン原子系をテストケースとして用います(分子モデリングソフトTinker[13]をもちいて、MM3力場でNVTアンサンブルを50Kで50ps実行しました)。図2を参照してください。

図2：密度行列の分割と再構築の精度の確認に用いた系。ネオン原子の10Å ³ボックス。座標は古典分子動力学により得た。

この系を1コア原子サブシステムに分割して、式(4)で定義されたパーティション行列を用います。系のエネルギー収束性をハロ半径の関数として表1に示しました。

Radius of Halo/Å	ED&C-Etrad/ millihartree cell-1
0.1	17.3
3.0	5.1
4.5	2.6

表1：ハロ半径を変化させた場合のD&CアルゴリズムのDFTエネルギー収束性。E_D&CはD&Cアルゴリズムによるエネルギー、E_tradはCRYSTAL標準のハミルトニアン行列対角化によるエネルギー。

この表から解る通り、ハロ半径が増加するにしたがって、エネルギーは標準的なCRYSTALの計算で用いられる伝統的なハミルトニアン対角化による結果に収束していきます。これはこの系の原子間相互作用が弱いことを考慮すれば当然の結果ですが、さらに分割統治法が系の分割とサブシステムにおける密度行列の再構成を正しく行っていることも示しています。

4.性能テスト

系の増大に沿ってD&Cアルゴリズムの性能を測定するために、面心立方構造のネオン結晶の様々なスーパーセルについて密度行列を計算させました。系のサイズを変えて測定した密度行列の計算時間を図3に示します。

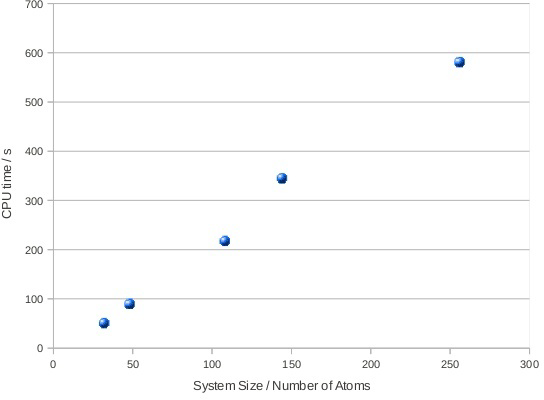
図3：系のサイズに対する分割統治法による密度行列計算時間。このアルゴリズムはほぼリニアなスケール性を示している。

ほぼリニアなスケール性が示されています。線形からのずれは系のフェルミエネルギー計算に起因します。図4はサブシステムの電子状態の準備と計算時間を示しています。

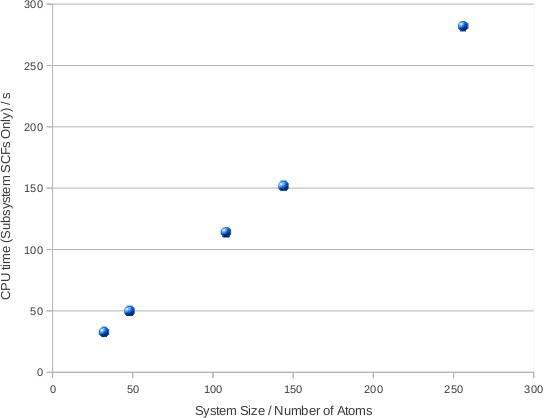
図4：全てのサブシステムに対するD&CアルゴリズムのSCF収束に掛かるCPU時間。ほぼ完全な線形スケール性を示している。フェルミエネルギー計算の効率化には更に調査が必要である。

この図からほぼ完ぺきな線形スケール性が見て取れます。また、計算時間の多くをフェルミエネルギー計算が占めていることもわかります。すなわちフェルミエネルギー計算の改善が今後の優先的な作業となります。

5.その他の有用な結果

5.1 タスク並列

CRYSTALへタスクファーミング機能を追加しました。この機能はD&Cアルゴリズムにとって本質的なものです。サブシステムの電子状態を順番に解いていくのは効率的ではありません。その他にもCRYSTALがタスクファーミングから得られる利点が複数あります。特にCRYSTALは、振動周波数やフォノン分散のために数値的な有限差分を使って、原子座標に関するポテンシャルエネルギー表面の2次微分を計算します。この計算は、タスクファーミングを用いてHPCリソース上で最大限の速度改善を図るのに非常に適しています。本プロジェクトの一部として導入されたタスクファーミングの有効性に関して、トリノ大学のMatteo Feraboneにより調査されつつあります。

多くの問題は、複数の似通った原子系を探索したり比較することで研究されます。例えば、インペリアルカレッジ・ロンドン校の共同研究者らは、黄銅鉱に含まれる成分元素の化学ポテンシャルが変化する場合の相図を作成しています。この手の計算では、似てはいるがそれ自身が独立な多数の計算実行が必要なため、本プロジェクトで導入されたタスクレベルの並列化により利得を得ることが出来るでしょう。

5.2 密度行列の初期値の改良

ガウス型基底関数を用いた電子構造計算コード利用の問題の一つに、SCFの収束性が初期値の品質に依存している点が挙げられます。本プロジェクトで開発されたコードは、密度行列をより小さな(より簡潔かつ低負荷)計算で構築するように作成されました。このコードが役立つ場面は複数あります。例えば以下の場合です：

1. 分子性結晶：初期電子密度は成分分子の収束した電子状態から作成される。
2. DNA、たんぱく質、高分子などの巨大分子：初期電子密度はモノマー分子の収束した電子状態から作成される。
3. 欠損の研究などでのスーパーセル：この場合はより複雑な利用で多少考察が必要になりますが、バルク電子密度はスーパーセルの「バルク様」領域の初期値を構築する際に利用可能です。

6.制限

本プロジェクトで導入されたCRYSTALのタスクファーミングには、プロセッサー数を割り切れる数のタスク数が必要です。これは各タスクで同数のプロセッサーが使用されることを意味します。さらに、もしタスクの負荷バランスがボトルネックとなったならば、ラウンドロビン方式の実装が必要となる可能性もあります。

CRYSTALのD&Cアルゴリズムの現状の実装には、長距離クーロン相互作用は含まれません。これは電荷分布の多重局展開と、多重局子が作る場へのサブシステムの埋め込みが必要になります。周期系の長距離静電ポテンシャルを正しく表現するには、Ewald和が用いられます。CRYSTALコード内にはこの作業を行うための仕組みが多くありますが、本プロジェクトでは時間的な制限のため実装は行いませんでした。

シリコンのような共有結合する周期系に対しては、D&Cアルゴリズムに対して、結合しない原子を生じさせないよう系の分割方法を修正する必要があります。ハロ半径で単純にサブシステムを分離すると、不適切なダングリングボンドを生じます。これはサブシステムの電子状態を全系と全く異なるものに変えてしまい、不適切なスピン分極を生じます。ダングリングボンドは水素などでキャップすることはできますが、自動でこの作業をさせるようにはまだ実装されていません。水素によるキャップが、ハロ領域サイズに関してD&Cアルゴリズムの収束性にどのような影響を与えるかも不明です。共有結合系の水素原子の位置を予測することは、X線結晶解析における生体分子の結晶構造決定で生じる問題と似ています。D&Cアルゴリズムでの水素原子のキャプ位置に対して、同じような経験的手法を用いる事が出来る可能性があります。

D&Cアルゴリズムをより一般的に利用可能にすることが必要です。現状この手法は、分子性結晶のような弱く結合した系しか対象とすることが出来ません。分子性結晶では様々な非経験的計算による研究の例があります[15,16]。こうした制限はありますが、このアルゴリズムは伝統的なハミルトニアン行列対角化手法とは別の利便性のある手法です。

7.結論

密度汎関数法による系のエネルギー計算のための分割統治法アルゴリズムが、CRYSTALに実装されました。共有結合系やイオン系へこのアルゴリズムを拡張することが望まれますが、この開発された手法は弱く相互作用をする系の非経験的計算研究に用いることが出来ます。またプロジェクトの結果として、タスクファーミング機能の追加、および密度行列の初期値の改良が実装されました。

謝辞

このプロジェクトは、NAG Ltd.が運営するHECToRの分散計算科学および工学(CSE)サービスの基に実行されました。英国の国立スーパーコンピューティング・サービスである、HECToR：英国リサーチ・カウンシル・ハイエンド計算サービスは、リサーチ・カウンシルを代行するEPSRCが管理しています。そのミッションは英国学術界の科学および工学の研究支援です。HECToRスーパーコンピューターは、UoE HPCx Ltd.およびNAG Ltd.のCSEサポートサービスにより管理運営されています。
著者はIan J. Bush博士および、Nicholas Harrison教授、Barbara Montanari博士、Leonardo Bernasconi博士に対し、本レポートへの貢献に対して感謝いたします。

文献

[1]	R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, M. Zicovic-Wilson, F. Pascale, B. Civalleri, K. Doll, M. N. Harrison, I. J. Bush, P. D'Arco, and M. Llunell, CRYSTAL09 User's Manual. University of Torino, Torino, 2009.
[2]	I. J. Bush, S. Tomi ć, B. G. Searle, G. Mallia, C. L. Bailey, L. Bernasconi, B. Montanari, J. M. Carr, and N. M. Harrison, \Parallel implementation of the ab initio CRYSTAL program: Electronic structure calculations for periodic systems," Proc. R. Soc. A, vol. 467, pp. 2112-2126, 2011.
[3]	R. Dovesi, B. Civalleri, R. Orlando, C. Roetti, and V. R. Saunders, Reviews in Computational Chemistry, vol. 21, ch. 1, pp. 1-125. John Wiley & Sons, 2005.
[4]	F. Cor à, "The performance of hybrid density functionals in solid state chemistry: the case of BaTiO3", Mol. Phys., vol. 103, pp. 2483-2496, 2005.
[5]	N. Martsinovich, D. R. Jones, and A. Troisi, \Electronic structure of TiO2 surfaces and effect of molecular adsorbates using different DFT implementations," J. Phys. Chem. C, vol. 114, pp. 22659-22670, 2010.
[6]	J. Graziani, A. M. Marquez, J. J. Plata, Y. Ortega, N. C. Hernandez, A. Meyer, C. M. Zicovich-Wilson, and J. F. Sanz, "Comparitive study on the performance of hybrid DFT functionals in highly correlated oxides: The case of CeO2 and Ce2O3", J. Chem. Theory Comput., vol. 7, pp. 56-65, 2011.
[7]	W. Kohn, "Density functional and density matrix method scaling linearly with the number of atoms", Phys. Rev. Lett, vol. 76, p. 3168, 1996.
[8]	C.-K. Skylaris, P. D. Haynes, A. A. Mosto, and M. C. Payne, "Introducing ONETEP: Linear-scaling density functional simulations on parallel computers", J. Chem. Phys., vol. 122, p. 084119, 2005.
[9]	D. R. Bowler, T. Miyazaki, and M. J. Gillan, "Recent progress in linear scaling ab initio electronic structure techniques", J. Phys.: Condens. Matter, vol. 14, p. 2781, 2002.
[10]	B. O. Cankurtaran, J. D. Gale, and M. J. Ford, "First principles calculations using density matrix divide-and-conquer within the SIESTA methodology", J. Phys.: Condens. Matter, vol. 20, p. 294208, 2008.
[11]	W. Yang, "Direct calculation of electron density in density-functional theory: Implementation for benzene and a tetrapeptide", Phys. Rev. A, vol. 44, pp. 7823-7826, 1991.
[12]	F. Shimojo, R. K. Kalia, A. Nakano, and P. Vashishta, "Embedded divide-and-conquer algorithm on heirarchical real-space grids: parallel moleculear dynamics simulation based on linear-scaling density functional theory", Comp. Phys. Comm., vol. 167, pp. 151-164, 2005.
[13]	http://dasher.wustl.edu/ffe/.
[14]	J. de Smedt, W. H. Keesom, and H. H. Mooy, "On the crystal structure of neon", Koninklijke Nederlandse Akademie van Wetenschappen, Series B, vol. 33, pp. 255-257, 1932.
[15]	K. Hannewald and P. A. Bobbert, "Ab initio theory of charge-carrier conduction in ultrapure organic crystals", Appl. Phys. Lett., vol. 85, p. 1535, 2004.
[16]	B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano, and P. Ugliengo, "B3LYP augmented with an empirical dispersion term (B3LYP-D*) as applied to molecular crystals," CrystEngComm, vol. 10, pp. 405-410, 2008.