ニューメリカルアルゴリズムズグループ(nAG)はユーザへ自動微分法の先進性を提供するために、アーヘン大学 Uwe Naumann 教授1 と密接に連携しています。
(2015年11月掲載)
概要
自動微分、Algorithmic differentiation あるいは Automatic differentiation(AD)は、正確(マシン精度)かつ効率的に数値計算プログラムの出力の入力に関する感度を計算する方法です。AD のフォワードあるいはリバースという2つの基本モードおよびその組合せは、各々ヤコビアンあるいはその転置行列およびヘッシアン行列とベクトルとの積を生成します。
本論
数値シミュレーションは、計算機科学や計算工学と同じく計算金融工学において重要な役割を果たしています。グラジェント、(射影された)ヤコビアン、(射影された)ヘッシアンおよびより高次の導関数で定義された感度は、数値モデルやそのパラメータの最適化のために、元のシミュレーションから望ましい状態へ遷移させる際に必要となります。こうした量は、多くの成功した例 [1,2,3] で示されているように、AD[5] によりマシン精度で計算が可能です。AD は、多変量非線形ベクトル関数 $F:\mathbb{R}^n→\mathbb{R}^m$ をコンピュータプログラムとして実装する手法です。ここで、$\mathbf{y}=F(\mathbf{x})$ を考えましょう:ヤコビアンを $F'=F'(\mathbf{x})$、ヘッシアンを $F''=F''(\mathbf{x})$ と記すことにします。AD のフォワードモードは、$F$ を tangent-linear モデルへ変換します。
\begin{equation*} \dot{F}(\mathop{\mathbf{x}}^↓,\mathop{\dot{\mathbf{x}}}^↓,\mathop{\dot{\mathbf{y}}}_↓) \quad where \quad \dot{\mathbf{y}} = F'\cdot\dot{\mathbf{x}} \quad. \end{equation*}
上に付した下向き矢印は入力です。下に付した下向き矢印が出力です。一連の $F'$ を行として、$\dot{x}$ を $\mathbf{R}^m$ のカルテシアン基底ベクトルに渡って計算します:tangent-linear モデルの全ヤコビアン計算は、有限差分商("bumping")による数値近似と同程度のオーダー $O(n)$ 程度の複雑さを持ちます。一方向の一次微分感度(例えばある方向への Delta の射影)は、$F$ の計算コストのほぼ 2,3 倍になります。
AD のリバースモードでは、$F$はアジョイントモデルに変換されます。
\begin{equation*} \bar{F}(\mathop{\mathbf{x}}^↓,\mathop{\bar{\mathbf{x}}}_↓^↓,\mathbf{\bar{\mathbf{y}}}^↓) \quad where \quad \bar{\mathbf{x}} = \bar{\mathbf{x}}+\bar{\mathbf{y}}\cdot F' \quad. \end{equation*}
$F'$ の計算には、入力で $\bar{\mathbf{x}}$ を $0$ にセットして、$\bar{\mathbf{y}}$ を $\mathbf{R}^m$ のカルテシアン基底ベクトルに渡って計算します:スカラー関数のグラジェント計算は、$F$ の計算複雑さに定数2 を掛けたコストで求められます。この高速計算能力は、大規模非線形最適化($n\gg 1$)での感度計算手法にとって重要です。現実的な問題解決に対して、先述したシミュレーションから最適化への遷移は他の方法では不可能です。
二次微分のグリークス(例えばガンマ)は、AD のフォワードとリバースの4つの組合せで計算可能です。記述を簡単にするために、ヘッシアンテンソルを含む積の定義を避けるため、$m=1$ を仮定します。関数の値 $y$ と全ての感度は、太字でないスカラーとなります。フォワード-over-リバースモードは、ヘッシアン-ベクトル積に適したやり方です。これは $F$ を二次微分アジョイントモデルへ変換します。
\begin{equation*} \dot{\bar{F}}(\mathop{\mathbf{x}}^↓,\mathop{\dot{\mathbf{x}}}^↓,\mathop{\dot{\bar{\mathbf{x}}}}_↓^↓,\mathop{\bar{y}}^↓,\mathop{\dot{\bar{y}}}^↓) \quad where \quad \dot{\bar{\mathbf{x}}} = \dot{\bar{\mathbf{x}}} + \dot{\bar{y}}\cdot F'(\mathbf{x}) + \bar{y}\cdot F''(\mathbf{x})\cdot \dot{\mathbf{x}} \quad. \end{equation*}
ヘッシアンとベクトル $\dot{\mathbf{x}}$ の積は、$\dot{\bar{\mathbf{x}}}=0$、$\dot{\bar{y}}=0$、$\bar{y}=1$ として、そのアジョイントコードの約 2 倍のコストで計算できます。言い換えればリバース-over-フォワードモードは、同等の計算コストで同じ結果を生成します。
もしリバースモードが出来ない場合は、$F$ の tangent-linear モデルへフォワードモードを適用することにより計算すべきでしょう。
\begin{equation*} \tilde{\dot{F}}(\mathop{\mathbf{x}}^↓,\mathop{\dot{\mathbf{x}}}^↓,\mathop{\tilde{\mathbf{x}}}^↓,\mathop{\tilde{\dot{y}}}_↓) \quad where \quad \tilde{\dot{y}} = \dot{\mathbf{x}}^T \cdot F''(\mathbf{x}) \cdot \tilde{\mathbf{x}} + F'(\mathbf{x}) \cdot \tilde{\dot{\mathbf{x}}} \quad. \end{equation*}
このヘッシアンは、$\tilde{\dot{\mathbf{x}}}=0$として、$\dot{\mathbf{x}}^T$ を初期化し、$\tilde{\mathbf{x}}$ を $\mathbb{R}^n$ のカルテシアン基底ベクトルに対応させて逐次計算します。この方法は $O(n^2)$ の計算コストが掛かり、実際上は実用的ではありません。
AD のロバストで効率的な実装が、最先端の数値シミュレーション手法において重要となります。この技法を利用すれば、シミュレーション・ソフトウェアの開発サイクルの短縮され、数値計算スキームの効率とロバスト性を高め、シミュレーションコードの長期のメンテナンス性が改善されます。
AD を使う3つの理由
有限差分による感度の近似は、ある場合には満足する結果を生じるでしょう。しかしながら、AD がグリークスを計算するための唯一の現実的なアプローチである状況が、以下に述べる3種類あります。
1. 有限差分の不正確性がユーザのアルゴリズムの収束性に悪影響を与えるため、正確な感度が必要な場合。
2. グラジェントの現実的な計算方法として有限差分あるいはフォワード感度計算を適用するには問題の次元 $n$ が大きすぎ、よりコストの低いグラジェント計算が必要な場合。
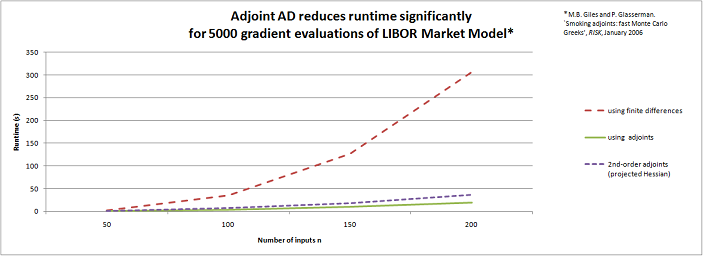
図1:アジョイント自動微分の優位性
ここで、セキュリティの感度計算のために LIBOR マーケットモデル [4] へ、リバースモード AD を適用してみました。5千個のデルタの計算に必要な時間は、有限差分の場合 $n$ に依存して増大しますが、アジョイントモードの場合は非常にゆっくりとした増加($n$ に依存しない)にとどまります。図1にこの結果を示します。
3. 数値計算モデルは、現在進行形の研究開発の結果からの洞察によって、常に変化するでしょう。その時には、対応する感度計算コードも更新が必要ですが、それには人月工数がかかります。よって感度計算コードの(部分的にも)自動生成する AD ソフトウェアツールが必要となるでしょう。
(補注):
1 LuFG Informatik 12: Software and Tools for Computational Engineering(STCE), Department of Computer Science, RWTH Aachen University, 52056 Aachen, Germany
2 実装や使用言語に依存して、このファクターは 3 倍あるいはそれ以上になります:典型的には直截的に得る場合より 50 倍です。$F$ の実装された構造をさらに詳しく考慮すれば 20 倍になるでしょう。理論的な最小値である 3 倍付近に到達するには、アジョイントモードの高度なチューニングが必要です。これは複雑な問題に対しては高度にチャレンジングな問題になることがあります。このファクターの最小化は、世界的に現在進行形の様々な研究開発がなされています。リファレンスとして、サイト www.autodiff.org をご覧ください。
参考文献
[1] C. Bischof, M. Bücker, P. Hovland, U. Naumann, and J. Utke, editors. Advances in Automatic Differentiation, number 64 in Lecture Notes in Computational Science and Engineering, Berlin, 2008. Springer.
[2] M. Bücker, G. Corliss, P. Hovland, U. Naumann, and B. Norris, editors. Automatic Differentiation:Applications, Theory, and Tools, number 50 in Lecture Notes in Computational Science and Engineering, Berlin, 2005. Springer.
[3] G. Corliss, C. Faure, A. Griewank, L. Hascoet, and U. Naumann, editors. Automatic Differentiation of Algorithms - From Simulation to Optimization, New York, 2002. Springer.
[4] M. Giles and P. Glasserman. Smoking adjoints: Fast monte carlo greeks. RISK, January 2006.
[5] A. Griewank and A. Walther. Evaluating Derivatives. Principles and Techniques of Algorithmic Differentiation. Second Edition. Number 19 in Frontiers in Applied Mathematics. SIAM, Philadelphia, 2000.
