自動微分(AD)はプログラムの微分計算に対する新しい方法です。例えば、$\frac{\partial F}{\partial x_1}, \frac{\partial F}{\partial x_2},\ldots$ を計算する場合を考えます。ここで $F$ は関数として以下のプログラムコードで与えられています。
if (x1 < x2) then
F = x1 * x1 + x2 * x2 + exp(x3 * x3) + ...
else
F = x1 + x2 + x3 + ...
end if
自動微分は数学的に正確であり、マシン精度まで保証します。これまでは通常、微分は有限差分("bump and revalue" とも呼ばれる)によって推定されることが多いのですが、それは時間がかかり、正確性を欠くことがあります。対照的に、AD(特に、ADD(アジョイント AD))は僅かなコストで正確な微分を与えます。
ここで、様々な領域で用いられているアジョイント AD の幾つかの例を示します。
自動車工学
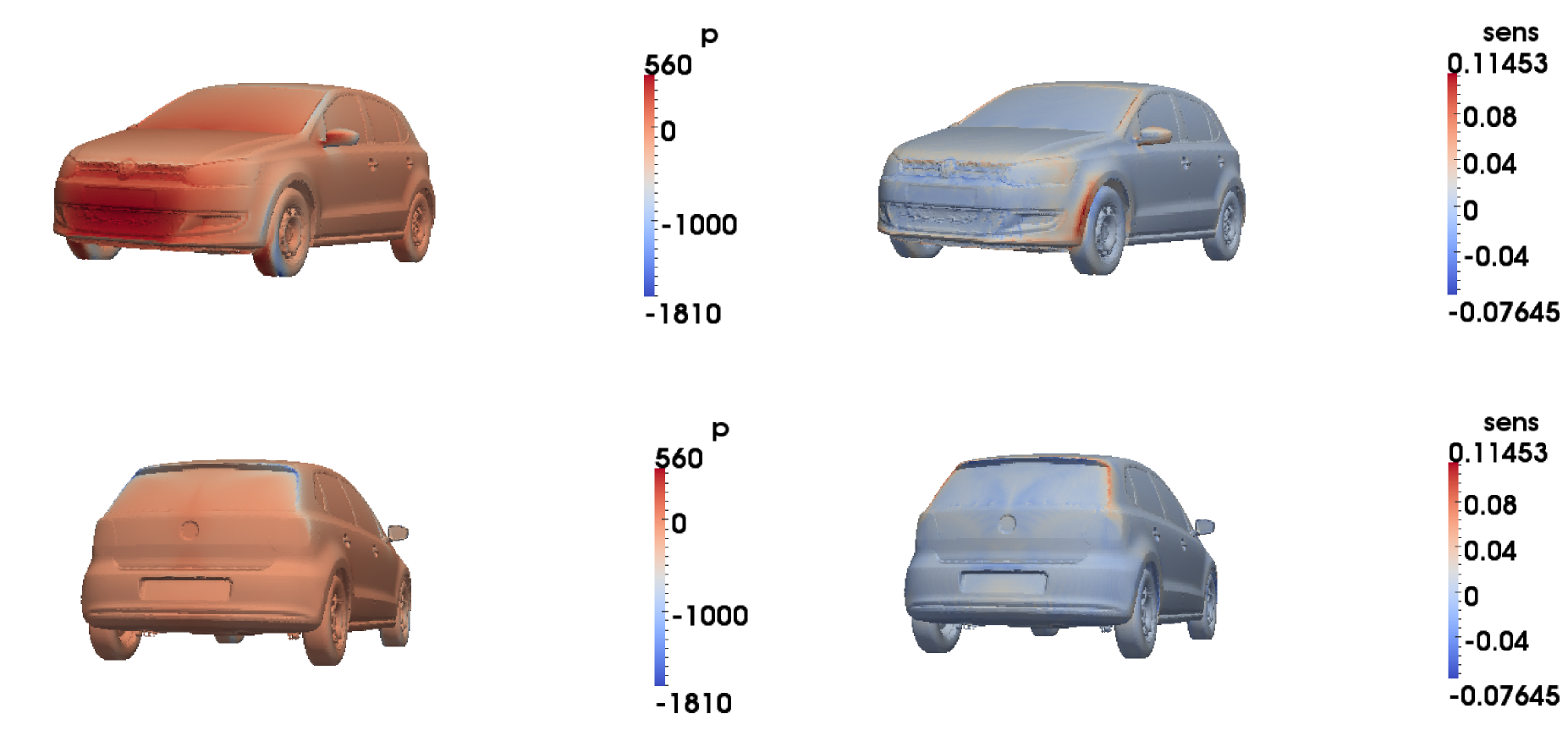
図1:高速(左図)および低速(右図)走行における自動車の表面形状に対する抗力係数の感度
AD は、大規模シミュレーションの感度解析による、形状最適化、インテリジェント設計および包括的なリスク研究を可能にします。
図1は、高速(左図)および低速(右図)走行における自動車表面上の各点での抗力係数の感度を示しています。このシミュレーションは、AD ツール "dco" 上に構築された、AD 化された OpenFOAM により実行されました。その表面メッシュは 5.5 百万セルで構成され、グラジェントベクトルは 18GB を占めました 1。
トップエンドのデスクトップマシンにおいて、通常のシミュレーションは 44 秒であったのに対し、その AD 化シミュレーションは 273 秒掛かりました。同じマシン上で、同等のグラジェント情報を得るために有限差分を用いたとすれば、おおよそ 5 年掛かると考えられます。
このようにして、グラジェント情報は今や自動車形状の最適に用いられ、その抗力を減少させる目的に利用できるようになりました。
1 Towara M and Naumann U $(2013)$. A discrete adjoint model for OpenFOAM. Procedia Comp. Sci. Volume 18.
気候モデリング
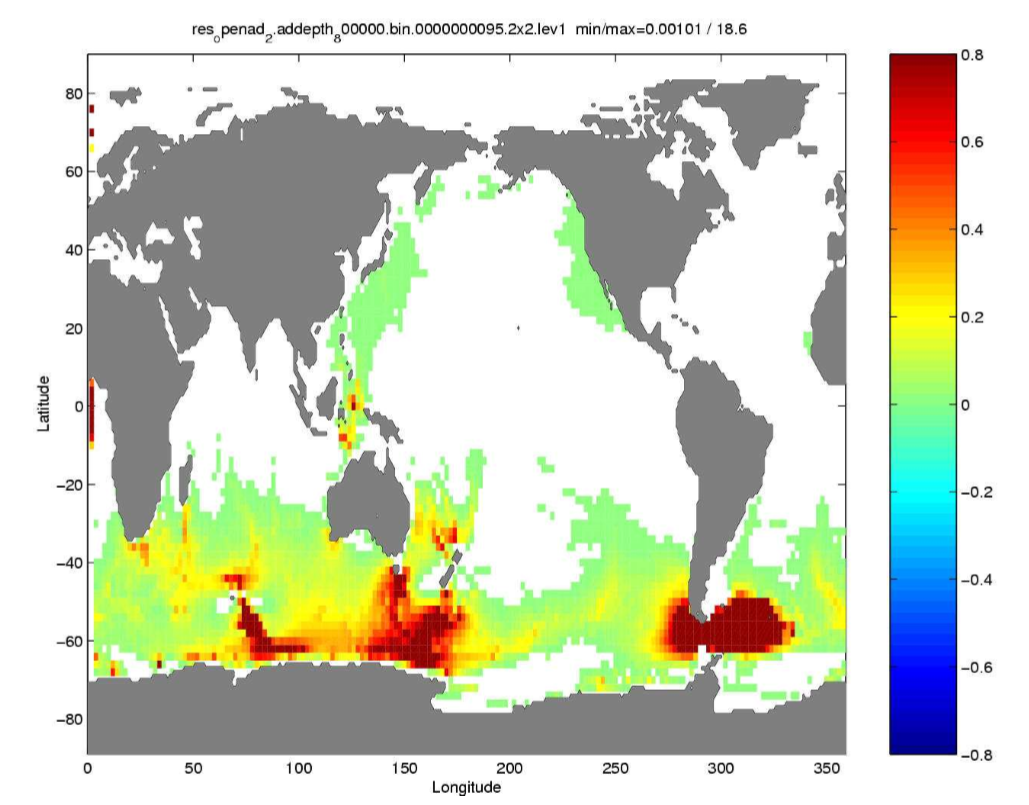
図2:海底地形の変化に対する、ドレーク海峡を流れる東西海水流の MITgcm モデル感度
AD は、気候変動の理解を助け、気象予報を改善します。
図2は、海底地形の変化に対する、ドレーク海峡を流れる海水流量の感度を示します。このシミュレーションは、スーパーコンピュータを用いた、AD 化された MIT Global Circulation Model の実行結果です。海洋は 64,800 グリッドのメッシュで構成されました 2。
有限差分によりそのグラジェントを得るのに、1.5 か月かかりました。アジョイント AD によるコードは、このグラジェントを 10 分未満で計算しました。
グラジェント情報は、気候予測をより精密化するために利用でき、さらにグローバルな気象、例えば、そのドレーク海峡から遠く離れているにも関わらず、南太平洋の端やインドネシア海流に高い感度をもっていることの理解に役立ちます。
2 Utke J, Naumann U, Wunsch C, Hill C, Heimbach P, Fagan M, Tallent N and Strout M. $(2008)$. OpenAD/F: A modular, open-source tool for automatic differentiation of Fortran codes. ACM Trans. Math. Softw, 34(4) 18:1-18:36.
ファイナンス
AD および ADD は、リアルタイムリスク管理や、xVA のような量のヘッジを可能にする複雑な金融商品の感度を迅速に得るために、金融工学においても使用されています。
ここで、ファイナンスで用いられる典型的なコードである、モンテカルロ法と偏微分方程式に関する論文から、幾つかの結果を示します 3。
| モンテカルロ法 | |||||
|---|---|---|---|---|---|
| $n$ | $f$ | cfd | AD | $\frac{\tt AD}{f}$ | $\frac{\tt cfd}{\tt AD}$ |
| 34 | 0.5s | 29.0s | 3.0s (2.5MB) | 6.0x | 9.7x |
| 62 | 0.7s | 80.9s | 5.1s (3.2MB) | 7.3x | 15.9x |
| 142 | 1.5s | 423.5s | 12.4s (5.1MB) | 8.3x | 34.2x |
| 222 | 2.3s | 1010.7s | 24.4s (7.1MB) | 10.6x | 41.4x |
| 偏微分方程式 | |||||
| 34 | 0.6s | 37.7s | 11.6s (535MB) | 19.3x | 3.3x |
| 62 | 1.0s | 119.5s | 18.7s (919MB) | 18.7x | 6.4x |
| 142 | 2.6s | 741.2s | 39s (2GB) | 15.0x | 19x |
| 222 | 4.1s | 1857.3s | 60s (3GB) | 14.6x | 31x |
表1:モンテカルロ法および偏微分方程式に対して、グラジェントサイズ "n" の関数として表した必要な実行時間とメモリ
表1は、典型的なファイナンスアプリケーション(ローカルボラティリティモデルでのオプションプライシング、10K サンプルパス/空間点および 360 時間ステップ)での、中心有限差分に対する、"dco"を用いた一次のアジョイントコードの実行時間を示しています。
第 2 列の f はアプリケーションの通常の実行時間、cfd は中心有限差分、および AD は追加で必要なメモリ(tape サイズ)と共にアジョイント AD の実行時間を表します。この計算はラップトップで実行したため、重要なのは実行時間の比 AD/f と cfd/AD です。これらは AD が有限差分に比べ高速であることを示しています。
ファイナンスにおいては、このような微分情報がヘッジやリスク管理において頻繁に利用されるため、これらのグラジェントは一日に頻繁に計算が必要になります。
3 du Toit J and Naumann U $(2014)$. 数理ファイナンスにおける典型的な数値計算パターンへのアジョイント自動微分ツールの適用. nAG テクニカル・レポート TR3/14.
AD はコンピュータプログラムの数学的な微分を計算します。概念的にこのプロセスは直截的なものです。
- コンピュータは浮動小数点の加算、減算、乗算、除算のみを実行できる
- いかなる浮動小数点演算を行うプログラムも、特殊関数(例えば sin、cos、exp 等)の呼出しと共に、単純にこれら基本的な演算の組合せで構成されている
- これら全ての基本的な演算の微分を計算するのは容易である
- コンピュータプログラムの微分を得るために、チェインルール(合成関数の微分則)を用いることができる
プログラムコードを微分するこのプロセスは、2次、3次、4次あるいはさらに高階の導関数を生成するのに適用することができます。そのコードは、シンポリックに(極めて低いレベルで)微分されるため、この微分は数学的に正確で、マシン精度で計算することができます。
従来、微分値の推定には有限差分("bumping" とも言われます)が用いられますが、これらと比較して、AD は3つの明確な利点を提供します。
- 有限差分を正しく行う事が難しい場合がある:その関数に関する何らかの知識が必要な場合が多い
- 高次の有限差分は悪化することがある:AD はいかなる次数においても正確なグラジェントを与える
- アジョイントモードの AD(詳細は 自動微分をより詳しく を参照してください)は有限差分よりも桁違いに高速である
AD は概念的には単純ですが、自明でないコードへ適用するには高い技術が求められます。
AD を実業務で利用する際には、コードの実行と保守が容易に行える、高性能でロバストかつ柔軟性のあるツールが必要不可欠です。さらに、外部参照ライブラリへの依存がADを不可能にすることは明らかです。なぜなら AD はソースコードを直に操作するからです。実業務に耐え得る AD ツールはこのような依存関係を適切に処理する必要があります。(理想的には外部ライブラリのソースコードに対しても AD を適用し、完全な AD ソリューションを作成するなど)。
AD ツール
C++/Fortran 言語向けの演算オーバーロード AD ツールを提供します。このツールは、数百万行の、かつ単一スレッドデスクトップから大規模スーパーコンピュータに渡る様々なプラットフォームで実行される製品コードに対して適用されてきました。
- "dco" ツールは、nAG と RWTH Aachen 大学との協力により開発され、お客様のコードへ容易に統合できる高い柔軟性を持ちます。
- この柔軟性は、アジョイントコードのメモリ制限をほぼ任意に制御することを可能にする観点から重要な性質です。
- それはまた、dco アジョイント計算で GPGPU といったアクセラレータの利用を可能にします。
AD のための nAG Fortran コンパイラ
Fortran で書かれたシミュレーションプログラムのために、nAG Fortran コンパイラは、dco に対するプリプロセッサとしての機能を果たすように拡張されたバージョンが作られました。複雑なビルドシステムへの AD のシームレスな統合が容易になりました。オリジナルコードでのユーザによる修正量は、最小限か、あるいは全く不要にすることが可能です。
計算アルゴリズムの AD バージョン
nAG は、nAG ライブラリに見られるような計算アルゴリズムの AD バージョンを提供します。これら AD ルーチンは、最大の生産性を提供できるように、dco との互換性を持ちますが、自作 AD コードを含みいかなる AD ツールとの互換性を保つバージョンも提供することが出来ます。
AD を試すには
金融工学での AD の原理と、アジョイントコードにおけるメモリ問題を避けるテクニックが、nAG テクニカル・レポート TR3/14 の $(3)$ において議論されています。そのテクニカルレポートにおいて基礎となる例題プログラムは、ご希望により提供することが可能です。その例題プログラムには、dco のコピーと、読者自身のマシン上で実行可能な例題、および読者自身のコードへ dco を適用できるトライアルライセンスを含みます。
