ラップタイムシミュレーションの最適化
ラップタイムシミュレーションの速度と精度を向上させるために、自動微分(AD)が利用できることをご存知でしょうか?自動微分はパフォーマンスを最大100倍向上させます。つまり、同じ時間でより多くのラップ シミュレーションを繰り返すことができます。また、自動微分はより高い精度の1次および2次微分を提供できるため、シミュレーションの堅固性を向上させることができます。より高い精度は、オプティマイザーがより確実に最適解を見つけるのに役立ちます。
なぜ、このようなことが重要なのでしょうか?ラップシミュレーションはレースで広く使用されており、チームの競争力に不可欠なものです。また、収益性の向上に伴い、e スポーツでもラップシミュレーションツールの需要が高まっていることが確認されています。最終的に、ラップシミュレーションの価値は、その精度と生成できるデータ量にあります。
nAGは競争の激しいモータースポーツでの過去の経験から、成功する高性能なシミュレーションは、車両の物理的挙動を表す様々な数学的モデル、そして効率的なアルゴリズムとツールに依存することを理解しています。
この記事では、ラップシミュレーションを改善するために自動微分がどのように利用できるかについて、RWTHアーヘン大学およびFormula Student Team Ecurie Aixとのコラボレーションに基づくケーススタディとともに、もう少し詳しく説明します。この記事は技術的なものですが、いくつかのビジュアルを追加しました。イギリスのレーストラック、シルバーストーンのラップタイムシミュレーションの例については、以下のシミュレーションをご覧ください。
自動微分はモデル開発の柔軟性を維持し、実行時間を短縮し、堅固性を実現します
このケーススタディのモデルは、nAGがこれまでに参加した最先端の実装のモデルよりも単純なものですが、コアとなる数値的側面は類似しており、これらの手法と自動微分がもたらす利点は、他のモデルにも容易に投影することが可能です。自動微分による効率的で正確な微分計算は、様々なモデルの実装に柔軟に対応できるため、特にこのことが言えます。後ほど数値で示すように、自動微分を用いると、実行時間が最短になり、導関数の精度によってオプティマイザーの堅牢性が得られます。
このケース スタディでは、自転車の車両モデル、タイヤ モデル、支配エネルギー方程式を使用して、非線形最適化問題を設定しました。この問題は、目的関数と、線形 (ボックス) および非線形の制約によって定義されます。基礎となるモデルがどのようなものであるかの印象をえるために、それらの定義を見てみましょう。
レーストラックは、中心線の x 座標と y 座標、トラック幅、および摩擦係数に基づいて、N 個の評価ポイントで離散化されます。現在、高さ情報は含まれていません。トラックはクローズトラックであると仮定されますが、離散化を少し変更するだけで、オープントラックも実装できます。軌道上の積分が達成されたラップタイムとは無関係になるように、時間から弧長への変換が適用されます。
パラメータ空間は、最適化の対象となる 8*N 変数によって定義されます。 最適化の目的は、スカラー コストの関数によって記述されます (主目的がラップタイムで、二次的にオプションでスムーズなアクチュエータ入力を達成するため目的が追加されます)。すべての変数はボックス制約の影響を受け、さらに最適化は 9*N(非線形)制約の影響を受けます。
- 5*N制約は支配方程式を強制します(残差=0に関する等式制約)。
- 2*N制約は、前輪と後輪の最大タイヤ力を超えないように強制します(力の輪)。
- 2*Nのオプションの制約は、スリップ角が妥当なままであることを強制します(解においてこれはいずれにしても満たされますが、オプティマイザーのパフォーマンスを向上させることができます)。
導関数ベースのアルゴリズムで効率的な非線形最適化を実行するには、次の導関数情報が必要です。
- 目的関数の勾配(8*N エントリ)
- 制約関数のヤコビアン(スパース 9*N x 8*N 行列、16 バンドのバンド構造)
- ラグランジュのヘシアン(スパース 8*N x 8*N 行列、28 バンドのバンド構造)
nAG の最適化スイートに組み込まれたモデルの C++ 実装を使用しています。 オプティマイザーを実行するには、目的、制約、およびそれらの1次導関数と2次導関数を評価する関数を提供する必要があります。 導関数の計算に使用される方法に応じて、コーディングの労力、効率、および精度の特性は大きく異なります。
- 密な有限差分:
これは一見すると最も簡単な方法ですが、精度とパフォーマンスの問題がすぐに明らかになります。密な有限差分は、必要な導関数情報の完全セットに使用でき、少しの努力でコード化することができます。私たちが利用しているnAGライブラリに含まれるソルバーは、有限差分を内部的に実装しており、ユーザーは目的関数と制約をそれぞれ評価する関数をコールバックとして渡すだけで済みます。残念なことに、特に高次の微分情報の場合、精度に疑問があることがネックとなり、後述するように、オプティマイザが解を見出せないことがあります。 - スパース有限差分:
微分テンソルの多くはスパース構造を持っており、このスパース情報を利用することで、導関数の計算の際に大きな性能向上をもたらします。これは勾配 (通常は密度が高い) には何の役にも立ちませんが、制約関数のヤコビ行列とラグランジアンのヘッセ行列の計算に利用できますし、利用する必要があります。このためには、問題のスパース性に関する知識が必要です。それは既知であるか、あるいは自動微分により計算で求めることができます。より効率的な有限差分のためにスパース性情報を使用することは、実装に少し手間がかかりますが、はるかに効率的です。nAGのようなソルバーもスパース性を利用しています。ただし、精度の問題は依然として残ります。 - 手動微分/手書き派生コード:
使用するモデルが数学的表現を持っている場合、対応する感度モデルを記号的に導出することができます。この方法は、数学的・計算的な細部を最適に利用できる可能性があるため、最も効率的な実装につながるかもしれません。しかし残念ながら、これらを導き出すために必要なスキルと、それを実装するための労力は、通常、非常に大きなものになります。さらに、この労力は一度だけの投資ではなく、モデルやパラメータセットが変わるたびに、感度モデルやその実装も変わってしまいます。数値的な特性や導出・実装の正しさにもよりますが、通常、精度特性は良好です。 - 自動微分:
自動微分は、スパース有限差分と手動コーディングの利点を兼ね備えています。正確な微分を(マシン精度まで)計算し、1次導関数およびそれ以上の導関数に対して非常に優れたパフォーマンスを発揮し(特に、リバース モードとも呼ばれるアジョイント モードを使用することにより)、モデルの変更に関して柔軟です。つまり、自動微分を実装するには1回限りの投資が必要ですが、見返りとして、メンテナンスコストが非常に低く、効率が高く、精度が高いという利点があります。適度に大きなC++コードへの自動微分の最初の適用は簡単ではありません。プログラムの設計、サードパーティライブラリの使用、計算アーキテクチャ、並列化、およびその他の側面に関連する課題があります。これらの注意点を踏まえると、自動微分が特効薬ではないことがわかります。しかし、適切なツールと信頼できるサポートがあれば、これらのリスクを抑えることができ、その恩恵が迅速に得られます。
実装はC++で行われています。モデルの実装にはEigen、最適化にはnAGライブラリ、必要な導関数の計算にはdco/c++が使用されています。nAGライブラリは、線形代数の最適化アルゴリズムから補間に至るまで、さまざまな数値アルゴリズムを提供します。 dco/c++はnAGの自動微分ツールで、豊富な機能セットとクラス最高のパフォーマンスを備えています。
nAGライブラリとADを併用することで、どのような効果が得られるのか、以下のような実行時間の数字で実感していただければと思います。

シミュレーションで得られた結果が上の部分です。左側は最適なレースライン、右側はレーストラック上の様々なパラメータです。
ここで紹介する結果は、Formula Studentの大会規則、つまり、軽い自動車、低速、電動パワートレイン、高ダウンフォースのための高抗力などのモデルによって得られたものであることに注意してください。通常、このような大会はシルバーストーンよりもはるかに狭くタイトなトラックで実行されます。
最適化の実行には、nAGライブラリの内点法最適化ソルバーであるe04stcルーチンを使用しています。
次の図は、制約のヤコビアンのスパース パターンを示しています。(予想どおり) かなりの規則性がありますが、制約または離散化スキームを変更すると変化する可能性があります。 スパース性は、ヤコビアンの非ゼロ要素のみが計算されて格納されるという意味で利用されます。 Hessian には、ゼロ以外のエントリがさらに少なくなります。

dco/c++で微分を計算する場合、勾配の計算には1次のアジョイントモード(dco::ga1s<double>)、ヤコビアンには1次のタンジェントベクトルモード( dco::gt1v<double, 8>)、Hessian計算には2次のタンジェントベクトルオーバーアジョイントモード( dco::ga1s<dco::gt1v<double, 8>)が使われます。性能向上のため、すべての自動微分ベクトルモードに対して明示的ベクトル化(AVX2)を実装し、dco/c++の基本機能セットと比較して、与えられたコードでさらに40%の速度向上を達成しました。
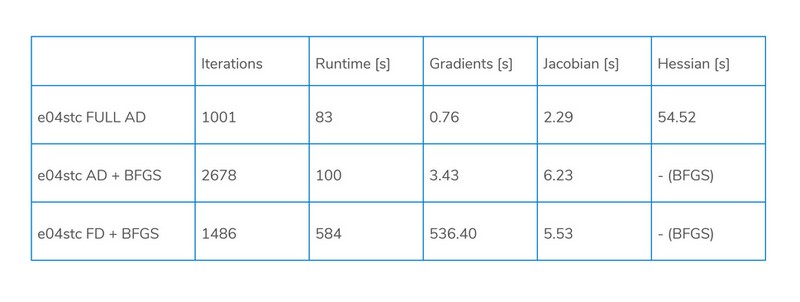
非線形最適化ルーチンe04stcについて、スパース有限差分とスパース自動微分の実行時間と収束動作を比較しました。シルバーストーンサーキットで1000個の離散化ポイント(ミュンヘン工科大学により離散化されたもの)を使用して最適化のテストケースを実行しました。
この特定のモデルでは、完全な自動微分バージョン(1次および2次導関数の自動微分)が最も信頼性が高いことがわかります。実行時間に関しては、自動微分による1次導関数の計算とBFGSアプローチによるHessianの近似のみが競争力を持っています。しかしこのアプローチが解に収束するかどうか、また何回反復するかは、非線形目的の定式化におけるわずかな変更に非常に影響されやすくなっています。
完全なFD実装は、非線形目的の勾配が密な場合、競争力がなく、AD + BFGSバージョンと同じ信頼性の問題に悩まされます。
ADは、非常に低いメンテナンスコスト、効率、高い精度を維持しながら、多くの柔軟性をもたらします。nAGは、自動微分だけでなく、最も効率的なツールやターゲットに合わせたサポートを提供します。nAGをパートナーにすることで、数値計算やハイパフォーマンスコンピューティングの専門家を利用することができます。
このブログを楽しんでいただけたら幸いです。nAGライブラリ、オプティマイザ、nAGの自動微分ソリューションについてもっとお知りになりたい場合は、ご遠慮なくご連絡ください。
ブログ執筆者: Markus TowaraおよびJohannes Lotz
