自動微分を使用すると、ハミルトニアンモンテカルロ(HMC)のサンプリングがより効率的になります
マルコフ連鎖モンテカルロ(MCMC)に関する我々の最近の論文で、時系列データからベイズ不確実性を定量化する方法 をご確認ください。またそれに 付属するコード を、nAG の GitHub でご確認ください。
nAG の AD ツールである dco/c++(RWTH アーヘン大学との共同開発)は C++ コードを微分化します。このツールは、明確に定義された導関数を持つ任意の C++ コードの微分化が行えます。
今回は、HMC 用のオープンソース Stan ソフトウェアと dco/c++ を組み合わせ、既存の C++ コードベースを使用して、ベイジアン不確かさの定量化を行いました。開発者の労力は最小限で済み、dco/c++ の高度な機能を使用して性能を調整することができます。MCMC ベースの不確かさ定量化は、多くの実世界の問題には計算量が高すぎると長い間考えられてきましたが、これは変わりつつあります。nAG の AD ツールである dco/c++ は、この問題で重要な役割を果たします。
結果
我々の論文での具体的な発見は、AD と HMC の組み合わせが、代替手法よりも 3〜4 倍も大きい有効サンプルサイズにつながるということでした。MCMC の生サンプル・サイズは、バーンイン段階が終了した後、サンプラーが実行する反復回数(下記の例では 1,000 回)を単純に表したものです。有効サンプルサイズは、同じ MCMC チェインからのサンプル間の自己相関を考慮して生サンプルサイズを調整します。例えば、より高い CPU 時間を持つ MCMC サンプラーは、自己相関が少ないサンプルを生成し、その結果、事後分布のより正確な推定値を得ることができます。特に、我々は、No U-Turn Sampler(HMC サンプラー)が、我々がテストした他のサンプラーよりも自己相関の低いサンプルを生成することを発見した。また、HMC での導関数の精度を上げると、より低い自己相関、すなわち、より高い有効サンプルサイズが得られることもわかりました(表をご参照ください)。上記の理由から、有効サンプルサイズは、MCMC サンプラーの効率を測定する際に、CPU 時間よりも重要な指標であると言えます。
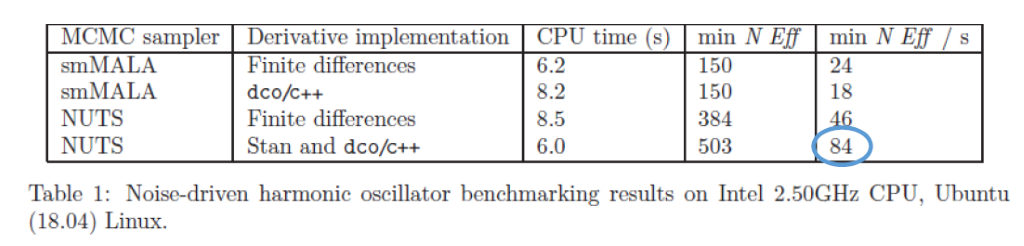
これらの結果を生成するために使用された例には、比較的少数の入力(5 個)しかありませんでした。 Adjoint 自動微分のCPU時間は、入力数とは独立して変化します。 つまり、有限差分の代わりに dco/c++ を使用すると、高次元の入力の問題で CPU 時間は 1 桁速くなる可能性があります。 このベンチマークでは、dco/c++ の基本機能のみが使用されています。より高度な dco/c++ 機能(たとえば、固有値計算のシンボリック Adjoint)を使用すれば、他にも CPU 時間を削減する余地がまだあります。
C++ コードベースをお持ちで、ベイズの不確かさ定量化を行う必要がある場合は、nAG の ソフトウェア をご覧ください。このアプローチは、MCMC から変分推論へ、そして C++ コードベースから Fortran コードベースへと拡張することができます。オープンソース・コミュニティや潜在的な産業用ユーザからのフィードバックを歓迎いたします。
