自動微分の事例

（2015年11月掲載）

前半の議論は GPU アプリケーションのアジョイント自動微分（前半部） をご覧ください。

6　FX バスケットオプションのアジョイント AD の実装

上述のセクション 3 のステージ 1 と 3 の CPU コードへ dco を用います。nAG C ライブラリ（例えば、内挿ルーチン）を呼び出す多くのコードにおいて、これらのルーチンの dco 適応可能バージョンを用います。アジョイントモードの dco は CUDA をサポートしないので、GPU のモンテカルロ計算カーネルに対しては異なる方法を取ります。ここで dco の外部関数インターフェースを使うこととします。これにより dco のテープに「ギャップ」を挿入し、外部関数がそのギャップを埋めるようにすることが出来ます。

コードが通常実行される時、モンテカルロ計算カーネルは外部関数として扱われます。ステージ 1 は dco データ型を用いて計算されます。ステージ 2 においては、最初に dco データ型から入力値（ローカルボラティリティのスプラインノットと係数、相関関数のコレスキー分解行列、自国および外国金利、等）を展開し、これらを GPU へコピーし、計算カーネルを起動し、最後に結果を CPU へ返します。こうしてこの結果は新しい dco データ型へ代入され、ステージ 3 へ計算は進みます。

テープがプレイバックされる時に、ステージ 2 のモンテカルロ計算カーネルのアジョイントモデルが実装された関数が必要となります。CUDA をサポートする AD ツールは無いため、この関数は手動で作成しなくてはなりません。モンテカルロ計算カーネルは大規模並列で行います。よってこのアジョイントモデルもまた大規模並列（各スレッドは一つかそれ以上のサンプルパスを独立して計算します）で、メモリに制約がある GPU 計算に適したコードです。このアジョイント GPU カーネルはテープがステージ 2 に達したときに実行されます：dco テープから入力するアジョイントデータが展開され、カーネルが起動し、出力したアジョイントデータは CPU にコピーされて dco テープに挿入され、その後計算は継続されます。

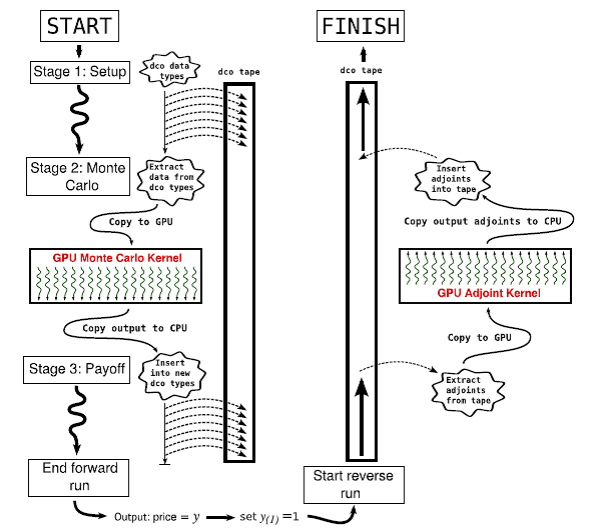
図１：アジョイント・プログラムの制御の流れ。ステージ 1 と 3 では、dco データ型はテープに記録されます。テープはステージ 2 でギャップを持ちます。アジョイント計算ではテープはプレイバックされ、手書きのアジョイント GPU カーネルはステージ 2 のギャップ内に有ります。

手動でアジョイントコードを作成することは困難に見えましたが、鍵となるのは、モンテカルロ計算カーネルを関数へ分解することであることが解りました。これらの関数のアジョイントモデルは比較的簡単に作成でき、これら個々のアジョイント関数をアジョイントカーネルとして繋ぎ合わせることが出来ました。最も困難な部分は、50 行余りの C のコードである三次スプライン評価関数でした（nAG C ライブラリ関数 e02bbc の GPU 版）。しかしながら一度この関数のアジョイントモデルが出来上がれば、三次スプライン評価コードは不変なことから、ライブラリとして他のプロジェクトでも用いる事が出来ます。

6.1 メモリの制御

セクション 4 で述べたようにアジョイント AD コードは、プログラムを逆向きに実行しなくてはならないため、中間計算の全てを保存するメモリ量が膨大になります。モンテカルロ計算コードでは、注意を怠ればすぐに数十から数百 GB になってしまいます。GPU では、メモリは高価で flops は安価なのが一般的な経験則であり、必要なもののみを保存してその他は再計算すべきです。

先述の式 $(6)$ において、簡単のために添え字 $(i)$ をはずして、アジョイント計算のために $\tau=n_T$ から $\tau=n_T-1$ まで逆向きに計算するとしましょう。ここに何が含まれているかを見るために、$(9)$ を $(6)$ へ代入して、$y_{(1)}$ が $log(S_{n_T})$ のアジョイントで、$x_{(1)}$ が $log(S_{n_T-1})$ のアジョイントと仮定しましょう（実際には $x_{(1)}$ は $r_d$、$r_f^{(1)}$、三次スプラインデータ、$log(S_{n_T-1})$、その他のアジョイントのベクトル $\mathbf{x_{(1)}}$ ですが、ここでは簡単のために一出力のみを考えます）。すると以下のようになります。

\begin{eqnarray} \frac{\partial t}{\partial log(S_{n_T-1})} &=&\frac{\partial log(S_{n_T})}{\partial log(S_{n_T-1})} \frac{\partial t}{\partial log(S_{n_T})} \tag{13} \\ &=&\left( 1+\sigma(S_{n_T-1},T-\Delta t) \frac{\partial \sigma(S_{n_T-1},T-\Delta t)}{\partial log(S_{n_T-1})} \\ +\sqrt{\Delta t}\mathbf{dZ}_{n_T} \frac{\partial \sigma(S_{n_T-1},T-\Delta t)}{\partial log(S_{n_T-1})} \right) \frac{\partial t}{\partial log(S_{n_T})} . \end{eqnarray}

この式から、$\sigma(x,t)$ が可逆でないために、$log(S_{n_T-1})$ の値が解らなければアジョイント計算が出来ないことが解ります。さらにこの値が解れば全ての他の値も計算できます（実際にこれは元のモンテカルロ計算カーネルが時間の正方向へ行うことです）。

よってアジョイントモデルの計算のために保存すべきデータは、全ての時間ステップ $\tau=1,…,n_T$、全ての資産 $i=1,…,N$ および全てのモンテカルロ・サンプルパス $j$ に対する値 $log(S_\tau^{(i)}(j))$ です。これらの値が分かれば、他のすべての値は計算できます。本報告ではスプライン計算負荷が高いため、ローカルボラティリティ $\sigma^{(i)}(S_\tau^{(i)}(j),\tau\Delta t)$ も保存対象としました。テスト問題の全てにおいて、GPU メモリを 420MB 程度考慮しました（セクション 7 を参照してください）。

6.2 競合状況と混合精度の扱い

モンテカルロ・カーネルの如何なるアジョイントモデルも競合する状況になります。これは先述の式 $(6)$ から明らかです：もしアジョイントモデルにおいて二つのサンプルパス $j$ と $j+1$ が並列で計算される場合、両方のスレッドが入力アジョイント $log(S_{\tau+1}^{(i)}(j))_{(1)}$ と $log(S_{\tau+1}^{(i)}(j+1))_{(1)}$ を使って、自国金利 $r_{d(1)}$ を更新しようとします。スレッドセーフにこれが出来ない場合は、データ衝突および/または結果不正が起きるでしょう。勿論このケースでは各スレッドが $r_{d(1)}$ のコピーを持つことが出来て、カーネル計算の終わりにこれらはスレッドセーフな形で問題なく更新されます。

しかしながらローカルボラティリティモデルでは、スプラインのアジョイントデータの更新の際に好ましくない競合状況が発生します。三次スプラインが如何に評価されるかを考えましょう。最も簡単には、三次スプラインはノットのセット $\lambda_1 \lt \lambda_2 \lt …\lt \lambda_{n_\lambda}$ および係数のセット $c_1,c_2,…,c_{n_c}$ で構成されます。ポイント $x$（$(3)$ 式の $x$ これは本質的にランダムな $log(S_\tau^{(i)})$ です）でのスプラインの値を得るためには、最初に $\lambda_k \leq x \lt \lambda_{k+1}$ を満たすインデックス k を見つけなければならない。そのスプライン値 $y$ はインデックス k で示される幾つかの $\lambda$ と幾つかの $c$ の関数 $f$ です。

\begin{equation*} y=f(x,\lambda_k,\lambda_{k+1},…,\lambda_{k+k_1},c_k,c_{k+1},…,c_{k+k_2}) 　\tag{14} \end{equation*}

ここで $k_1=k_2=3$ としましょう。式 $(8)$ から式 $(14)$ のアジョイントモデルは以下のようになります。

\begin{eqnarray} \left( \begin{array}{c} x \\ \lambda_k \\ \lambda_{k+1} \\ \lambda_{k+2} \\ c_k \\ c_{k+1} \\ c_{k+2} \end{array} \right)_{(1)} =y_{(1)} \nabla f(x,\lambda_k,\lambda_{k+1},…,\lambda_{k+k_1},c_k,c_{k+1},…,c_{k+k_2}). \tag{15} \end{eqnarray}

もし同時に他のスレッドがある $\lambda_{k+1} \leq x' \lt \lambda_{k+2}$ で同じ計算を実行した場合、これらのスレッドは同時にアジョイント $\lambda_{k+1(1)}, \lambda_{k+2(1)},c_{k+1(1)}$ を更新しようとするでしょう。また、$x$ と $x'$ はランダム変数なので、これらの競合が起こることを予測し得ません。

これを避ける一つの方法は、各スレッドにスプラインデータのアジョイントのコピーを持たせることです。しかしながら 4 万スレッドの GPU カーネルには数十 GB のメモリが必要となり、困難です。別のやり方に、各スレッドへ自身のコピーをシェアードメモリに与え、各スレッドブロックがそのスレッドらと同期して、スレッドセーフに結果を代入する方法があります。ここでの問題は、シェアードメモリで忽ち実行を終えてしまうか、最良の場合でも GPU プロセッサ毎に 1 スレッドブロックしか実行されず、性能が出ないことです。第3の方法は、各スレッドブロックに対して、シェアードメモリに自身のデータのコピーを与えて、競合を避けるようにスレッド間同期を工夫することです。しかしこれはコードが複雑化して性能は期待できないでしょう。第 4 の方法は、アジョイントをスレッドセーフに更新するのに、ハードウェア的アトミック操作（不可分操作）（注 b）を行うことです。この方法が良さそうですが性能は低下します（本報告の実装では少なくとも 4 倍遅いです）。

注 b：アトミック操作はスレッドセーフを保証します。もし２つのスレッドが同じ変数に不可分に加算を実行すると、その変数は正しい結果を含むことが保証されます。

本報告では、単精度かつ、アトミック操作の幾つかを組み合わせて（これらを用いなくとも実装が可能ですが、純粋にプログラミングしやすさのために利用します）、アジョイントを計算するスレッドにプライベート配列を用います。（補足：ステージ 1 と 3 の CPU での計算は倍精度です）文献 [2] において、GPU を用いた単精度、倍精度および混合精度でのモンテカルロ計算の性能と精度に対する影響を示しています。この文献で用いたアプリケーションについては、倍精度から単精度へ変更すると実行時間は半分になり、得られた結果は単精度の公差内でした。特にモンテカルロ予測の標準偏差は単精度の精度限界（ほぼ $10^6$）より大きなオーダーでした。単精度での計算、特に（変数を次々に加算していくような）微分の寄与を積算するアジョイントのようなものを計算する場合は特に注意が必要です。本報告のアジョイント計算においては、混合精度で $r_{d(1)}$ を計算しますが、これはその数値が比較的小さく、単精度で生じる丸め誤差が生じないためです。

ここで強調すべきこととして、アジョイント計算を単精度にしたのは単純に性能のためです。この計算はGPUを用いて倍精度でも可能です。

6.2.1 注意

上述の困った競合状況は、大きなシェアードメモリを用いて、モンテカルロ・サンプルパスを一つの時間ステップから次へ更新するにのみ生じます。これはローカルボラティリティ型のモデルの典型的な性質で、他の多くの金融モデル（例えば、ヘストンモデル）では生じないものです。これらのモデルでは、SDE を支配する幾つかのスカラー値が存在し、その入力変数のアジョイントの自身のコピーを各スレッドに与えることにより、競合状況は簡単に操作でき、計算結果の標準的な並列リダクション計算が実行可能です。これは効果的かつ簡便な方法です。

7　結果

微分計算の実行時間と精度について、全倍精度コードとの比較で示します。先述したように、CPU での計算は倍精度で実行され、GPU 計算は大部分が単精度ですが、１あるいは２つのアジョイント計算が倍精度です。

7.1 テスト問題

共通の重みを持つ次の通貨ペアの 1 年間のバスケットオプションを考えます：EURUSD, AUDUSD, GBPUSD, USDCAD, USDJPY, USDBRL, USDINR, USDMYR, USDRUB, USDZAR。スポットレートを 2012年9月のマーケットデータから取り、相関行列を推定しました。自国・外国両方の金利と、ストライク価格は簡単のためにゼロとしました。満期当り５つの FX クォートと FX レート当り７つの満期があり、これは総数で 438 に入力パラメータと 438 の計算すべき微分がある事を示します。

モンテカルロシミュレーションにおいては、360 時間ステップの各々に 1 万サンプルパスを使用しました。

7.2 ハードウェアとコンパイラ

計算プラットフォームには以下を用いました。

• CPU：Intel Xeon E5-2670：計算負荷状況下で 3.3GHz まで周波数アップ可能な基本周波数 2.6GHz の、20MB の L3 キャッシュを持つ 8 コアプロセッサー。
• GPU：NVIDIA K20X with 6GB RAM：GPU クロックは 700MHz、メモリバンド幅は約 200GB/s（CUDA SDK のバンド幅テストによる数値）。また、CUDA toolkit 5.5 を用いました。

7.3 実行時間と精度

上述の問題に対する結果は以下の通りです。

• 全実行時間：22.4ms
  - フォワード計算：367.0ms
  * GPU 乱数発生器：4.5ms
  * GPU モンテカルロカーネル：14.5ms
  - アジョイント計算(逆向き計算)：155.4ms
  * GPU アジョイント・モンテカルロカーネル：85.1ms
• GPU との間のメモリコピー時間：約 0.5ms
• dco はテープを構成するのに CPU メモリを 268MB 使用し、420MB の GPU メモリを使用した。

比較のため、参照としてのシリアル倍精度での dco を用いた tangent-linear モードの CPU 計算では、438 の微分を計算するのに 2 時間以上必要でした。tangent-linear モデルは有限差分と同程度の演算であり、グラジェントを有限差分で計算すると同程度の実行時間が必要になると考えられます。

倍精度計算と比べた混合精度計算の誤差をプロット（一つは対数プロット）したグラフを図２に示します。

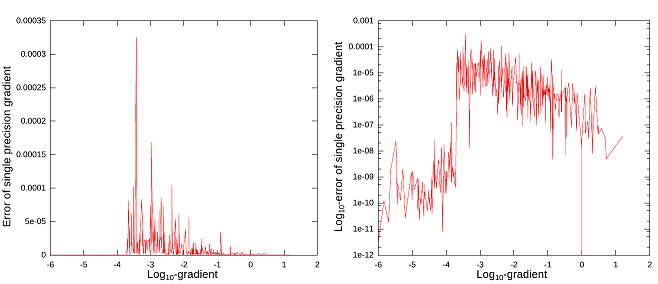
図２：グラジェントの対数に対する誤差と誤差の対数グラフ。誤差は式 $(16)$ で与えられ、対数は 10 を底とする。

グラジェントと誤差の絶対値を以下のように定義します。

\begin{eqnarray} err= \begin{cases} |g_{ref}-g_{mp}| & if|g_{ref}| \lt 0.0002 \\ \frac{max(g_{ref},g_{mp})}{min(g_{ref},g_{mp})}-1 & otherwise \end{cases} \tag{16} \end{eqnarray}

ここで、$g_{ref}$ は参照倍精度グラジェント、$g_{mp}$ は混合精度によるグラジェントです。グラジェントの多くは、絶対値において極めて小さく（これらの内 103 は $2×10^{-4}$ 以下）、これらに対しては相対的な差よりも絶対値として測りました。438 の内５つが $10^{-4}$ 以上で、16 個が $5×10^{-5}$ 以上でした。よってその精度は単精度よりも少し良く、多くのグラジェント値は小さいものでした。

7.4 スケーリング性能

この問題を 2 万モンテカルロ・サンプルパスを用いて実行し、以下の結果を得ました。

• 全計算時間：611.6ms
• GPU モンテカルロ・カーネル：28.902ms
• GPU アジョイントカーネル：142.8ms
• dco がテープに用いた CPU メモリ：280MB

GPU モンテカルロ・カーネルは 2 倍、GPU アジョイントカーネルは 1.7 倍になりましたが、全計算時間は 1.17 倍でした。これは全体の約 66 %を占める比較的コストのかかるステージ 1 が原因であり、サンプルパス数には無関係な時間です。

バスケットの 5 資産のみに対して 1 万サンプルパスで問題を実行すると、以下の結果が得られました。

• 全計算時間：283.4ms
• GPU モンテカルロ・カーネル：6.6ms
• GPU アジョイントカーネル：58.7ms
• dco がテープに用いた CPU メモリ：135MB

計算時間はアジョイントカーネルが 1.4 倍となった以外は、ほぼ 2 倍となりました。これはスレッドセーフにアジョイントを計算する際の同期オーバーヘッドが原因です。

8　謝辞

著者らは、PSG クラスタの利用に関して NVIDIA 社に感謝の意を表します。

参考文献

[1] Naumann, U. $(2012)$, The art of differentiating computer programs. Siam.

[2] du Toit, J., Ehrlich, I. $(2013)$, Local volatility FX basket option on CPU and GPU. nAG Technical Report, https://www.nag.com/numeric/gpus/local-volatility-fx-basket-option-on-cpu-and-gpu.pdf

[3] Giles, M., Xiaoke, S. $(2007)$, A note on using the nVidia 8800 GTX graphics card　Research Report, available at http://people.maths.ox.ac.uk/gilesm/codes/libor/report.pdf

[4] Vandevoorde, D., Josuttis, N. $(2002)$, C++ templates: the complete guide. Addison Wesley.