製紙機械ヘッダー部の形状最適化：数値解析による検討

Jan Stebel
2007年7月16日

1. モデルの説明

我々は、紙製造機ヘッダーの後壁の最適な形状を見つけることに興味があります（図1）。ヘッダーは紙製造機のヘッドボックスの最初のコンポーネントであり、その機能は流体（水と木材繊維）を機械の幅全体に均等に供給し、高品質の紙を生産することです。最小化すべきコスト関数は以下の通りです：

$$J(\alpha ,v(\alpha ),p(\alpha )):={\int }_{{\mathrm{\Gamma }}_{out}}|v_2(\alpha )-v_{opt}{|}^2$$

ここで： - $\alpha$：後壁の形状を記述する関数 - $v(\alpha ),p(\alpha )$：混合物の速度と圧力 - $v_{opt}$：出口 ${\mathrm{\Gamma }}_{out}$ での目標速度

ヘッダーのドメイン $\mathrm{\Omega }(\alpha )$ は以下のように記述されます：

$$\mathrm{\Omega }(\alpha )=\{x=(x_1,x_2)\in {\mathbb{R}}^2;0<x_1<L,0<x_2<\alpha (x_1)\}$$

図1：ヘッダー $\mathrm{\Omega }(\alpha )$ の形状

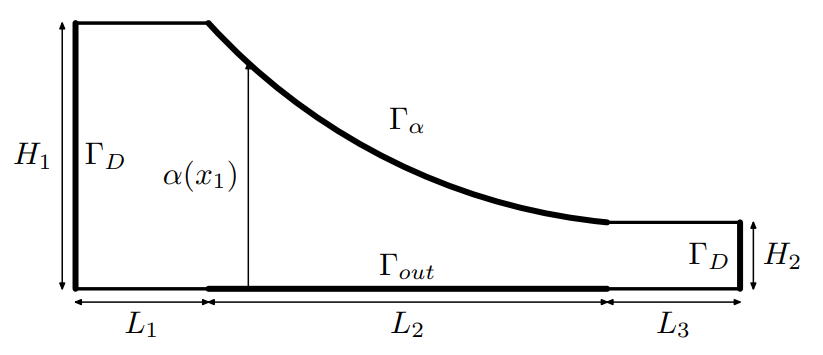
$$\begin{array}{rlr}{L}_1& L_2& L_3\\ H_1& H_2& \alpha (x_1)\end{array}$$

$\mathrm{\Omega }(\alpha )$ が許容可能であるとは、$\alpha \in U_{ad}$ であることを意味し、ここで：

$$U_{ad}=\{\alpha \in C^{0,1}([0,L]);{\alpha }_{min}\le \alpha \le {\alpha }_{max},\alpha |[0,L_1]=H_1,\alpha |[L_1+L_2,L]=H_2,|{\alpha }^{\prime }|\le \gamma \text{ a.e. in }[0,L]\}$$

ここで、$L:=L_1+L_2+L_3$ です。

混合物の動きは、一般化されたナビエ・ストークス系を用いてモデル化されます：

$$\begin{array}{rl}-\text{div}T(p,D(v))+\rho \text{div}(v\otimes v)& =0\\ \text{div}v& =0\end{array}\text{in}\mathrm{\Omega }(\alpha )$$

ここで： - $v:=v(\alpha )$：速度 - $p:=p(\alpha )$：圧力 - $\rho$：流体密度 - $T$：応力テンソル

応力テンソル $T$ は以下のように定義されます：

$$T(p,D(v))=-pI+2\mu (|D(v)|)D(v)$$

ここで： - $\mu (|D(v)|):={\mu }_0+{\mu }_t(|D(v)|)={\mu }_0+\rho l_{m,\alpha }|D(v)|$ - ${\mu }_0>0$：定数層流粘度 - ${\mu }_t$：乱流粘度

関数 $l_{m,\alpha }$ は代数的乱流モデルにおける混合長を表します：

$$l_{m,\alpha }(x)=\frac{1}{2}\alpha (x_1)(0.14-0.08{(1-\frac{2d_{\alpha }(x)}{\alpha (x_1)})}^2-0.06{(1-\frac{2d_{\alpha }(x)}{\alpha (x_1)})}^4)$$

ここで $d_{\alpha }(x)=min\{x_2,\alpha (x_1)-x_2\}$ です。

境界条件：

$$\begin{array}{rl}v& =0\text{on}{\mathrm{\Gamma }}_f\cup {\mathrm{\Gamma }}_{\alpha }\\ v& =v_D\text{on}{\mathrm{\Gamma }}_D\\ v\cdot \tau & =v_1=0\text{on}{\mathrm{\Gamma }}_{out}\\ T_{22}:=T\nu \cdot \nu & =-\sigma |v_2|v_2\text{on}{\mathrm{\Gamma }}_{out}\end{array}$$

ここで： - $\nu$：単位法線ベクトル - $\tau$：${\mathrm{\Gamma }}_{out}$ への接線ベクトル - $\sigma >0$：吸引係数

条件 $T_{22}$ は複雑な形状の均質化から来ています。

2. 近似とテスト結果

状態問題は、三角形メッシュ上の有限要素法を用いて離散化されます。$J$ の $\alpha$ に関する勾配を計算するために、随伴方程式技法が適用されます。必要なすべての偏導関数は自動微分によって提供されます。

関数 $\alpha$ はベジエ関数 ${\alpha }_M$ によって近似されます。許容性は単純な境界条件によって強制されます。

これにより、非線形の境界制約付きプログラミング問題となります。nAG Cライブラリのルーチン e04wdc がこれを解くために使用されました。

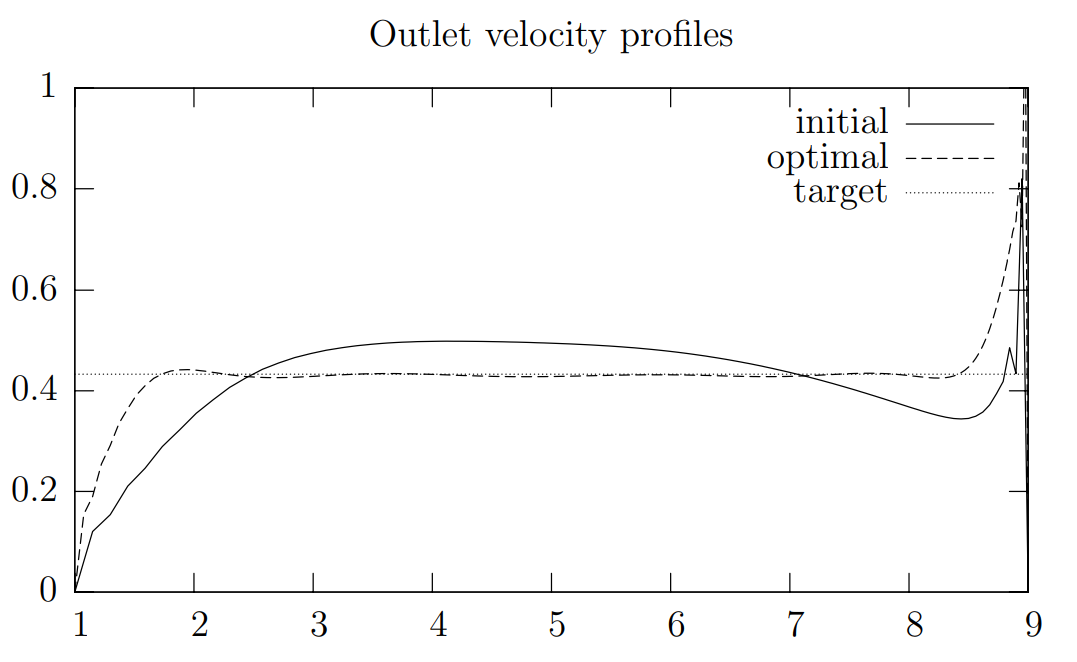
使用されたパラメータ： - $L_1=1.0$ - $L_2=8.0$ - $L_3=0.5$ - $H_1=1.0$ - $H_2=0.1$ - ${\alpha }_{min}=H_2$ - ${\alpha }_{max}=H_1$ - ${\mu }_0={10}^{-3}$ - $\rho ={10}^3$ - $\sigma ={10}^3$ - 入口速度：$v_D{|}_0\times (0,H_1)=(4(1-(2x_2/H_1-1{)}^8),0)$ - 目標速度：$v_{opt}=-0.433$

最適化は線形的に先細りの形状から開始しました。初期形状と最適形状を図2に示します。

図2：初期形状と最適形状

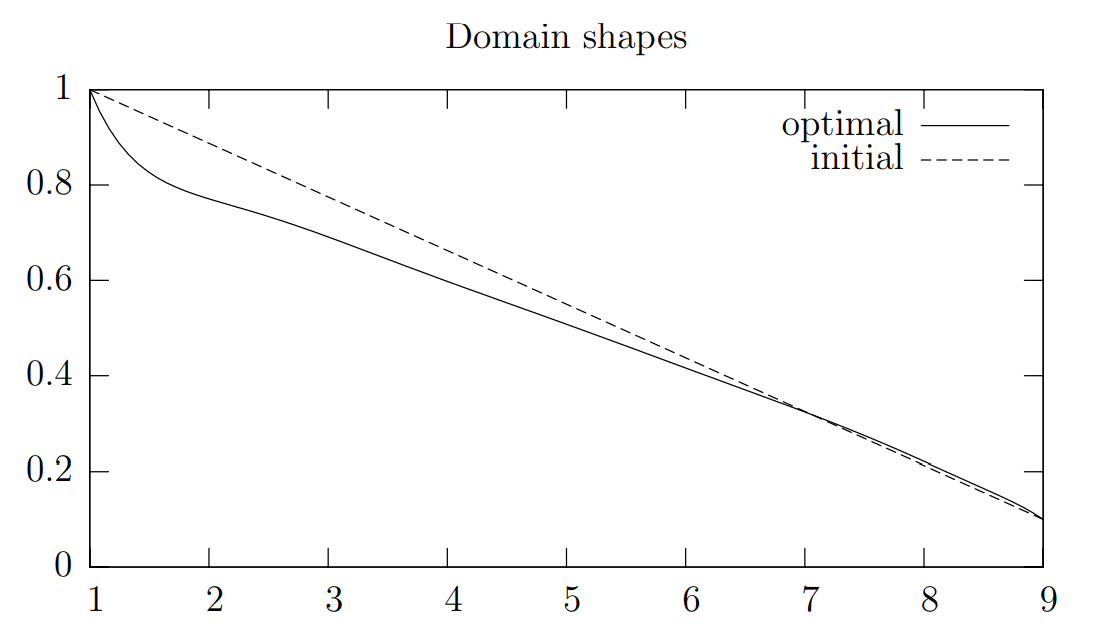
nAGルーチンは73回の反復後に、最適性誤差が ${10}^{-6}$ より小さい解を見つけました。

図3：初期および最適速度プロファイル

3. 結論

nAG最適化ルーチンは問題の要件を成功裏に満たしました。

参考文献

[1] P. E. Gill, W. Murray, and M. A. Saunders. SNOPT: An SQP Algorithm for Large-scale Constrained Optimization. SIAM J. Optim., 12:979-1006, 2002.