John Morrissey and Brian Spector
The Numerical Algorithms Group
February 18, 2015
要旨
nAGライブラリには、金融業界の大規模なポートフォリオ最適化と選択問題を解決するために使用できる、強力で信頼性の高い最適化ツールが多数あります。以下は、ポートフォリオ最適化で使用される表記法と技術の紹介です。いくつかのサンプル問題について議論し、適切なnAG最適化ツールを選択するためのヘルプを提供します。最後に、ポートフォリオ最適化における取引コストの扱いについてのセクションがあります。
1. はじめに
資産や株式の選択は、魅力的な投資を見つけるだけの問題ではありません。正しい資産ポートフォリオの設計は、人間の直感だけでは行えず、数値最適化技術の使用が必要です。ニューメリカル・アルゴリズムズ・グループ社(nAG)は、数値アルゴリズムに関する世界的に有名な企業であり、nAGの最適化ルーチンは産業界、商業界、学術界で広く使用されています。多くの主要金融企業や機関がnAG最適化ツールを使用して、ポートフォリオの選択、分散、再調整を行っています。また、ビジネススクールや経営大学院でも教育や研究に使用されています。
どの投資家も、投資からできる限り高いリターンを得たいと考えます。しかし、これは投資家が取ることができる、あるいは望むリスクの量とバランスを取る必要があります。期待リターンとリスク(分散または標準偏差で測定される)は、ポートフォリオの2つの主要な特徴です。残念ながら、高リターンの株式は通常、高リスクも伴います。
ポートフォリオのパフォーマンスは、ポートフォリオ内の個々のコンポーネントのパフォーマンスとは大きく異なる可能性があります。主要市場の株式から適切に構築されたポートフォリオのリスクは、ポートフォリオ内の個々の資産のリスクの合計の半分程度になる可能性があります。これは、個々の資産や株式間の複雑な相関パターンによるものです。優れた最適化ツールは、相関、期待リターン、リスク(分散)、およびユーザーの制約を活用して、最適化されたポートフォリオを得ることができます。nAG最適化ルーチンは、投資家の期待に合わせて最適化され、分散されたポートフォリオを提供できます。
ポートフォリオ最適化の数学的問題は、1950年代にハリー・マーコウィッツ教授によって始められ、彼は1990年にウィリアム・シャープ教授とマートン・ミラー教授と共にノーベル経済学賞を受賞しました。nAG最適化ツールは、古典的なマーコウィッツ最適化問題や多くの現代的な拡張を扱うことができます。nAGはまた、金融セクターに対して、ポートフォリオ最適化、自動微分、債券とオプションの価格設定、その他の分野に関連する数学的、数値的、およびプログラミングの問題を解決するためのコンサルティングサービスも提供しています。
ポートフォリオ最適化は、しばしば平均分散(MV)最適化と呼ばれます。「平均」という用語は、投資の平均または期待リターンを指し、「分散」はポートフォリオに関連するリスクの尺度です。数学的問題は様々な方法で定式化できますが、主要な問題は以下のようにまとめることができます:
- 指定された期待リターンに対してリスクを最小化する
- 指定されたリスクに対して期待リターンを最大化する
- 指定されたリスク回避係数を使用してリスクを最小化し、期待リターンを最大化する
- 期待リターンに関係なくリスクを最小化する
- リスクに関係なく期待リターンを最大化する
上記の問題には、線形、非線形、等式、または不等式制約がある可能性があります。最初の3つの問題は、本質的に数学的に同等です。4番目の問題は、慎重な投資家向けの最小分散解を与えます。これは他のポートフォリオとの比較やベンチマーキングにも使用されます。5番目の問題は、達成可能な期待リターンの上限を与えます。これも比較に有用です。
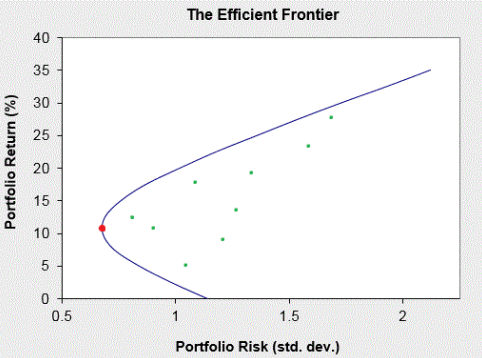
市場条件(例えば、期待リターンや資産間の相関)や投資家のリスク選好が変化した場合、ポートフォリオを再調整することが推奨されます。上記の問題のいずれも、既存のポートフォリオやベンチマークに対して解くことができ、ベンチマークのパフォーマンスに一致または上回るという考えがあります。上記の問題の解は平均分散(MV)効率的と呼ばれます。リターン-リスクグラフ上の効率的な点は、効率的フロンティアと呼ばれます。
新しいポートフォリオの購入やポートフォリオの再調整に関連する取引コストは、投資家にとって重要な金額を表す可能性があります。nAG最適化ルーチンは取引コストを扱うことができ、これらはポートフォリオの構成に大きな影響を与える可能性があります。
2. 表記法
ポートフォリオ最適化で一般的に使用される表記法を使用します:
- \(x\):ポートフォリオの重みのベクトル
- \(\mu\):期待リターンのベクトル
- \(\Sigma\):共分散行列(通常、過去のデータから計算される)
- \(l_i\):\(i\)番目の資産の下限
- \(u_i\):\(i\)番目の資産の上限
典型的な問題では、重みの合計が1になります(完全投資制約として知られています):
\[ \sum_{i=1}^{n} x_i = 1 \]
そして変数に対する制約:
\[ l_i \leq x_i \leq u_i \]
また、ある\(x_i\)が現金相当物に対応する可能性もあります。\(x_i \leq 0\)の場合、これはその資産の空売りに対応することに注意してください。
さらに、投資家は特定のグループの資産に対する線形制約を持つ場合があります。彼らは株式のサブセットにポートフォリオの最低50%を配分したいかもしれません。これは行列\(A\)を通じて定式化し、最適化ツールに入力することができます:
\[ L \leq A x \leq U \]
\(x_i\)の制約は一般的な線形制約の定義に含めることができますが、計算効率の理由から、我々はそれらを区別することを好みます。等式制約の場合、下限と上限は同じ値に設定されます。また、上限を\(\infty\)に、下限を\(-\infty\)に設定することも可能です。
3. 最適化問題の例
モデルを定式化する際、nAG最適化ツールが扱える目的関数と制約の組み合わせは数多くあります。以下に、より一般的な問題のいくつかを示します:
リスクの最小化(マーコウィッツモデル)
\[ \min_x x^T \Sigma x \]
これは、投資家が望ましいリターンレベルを設定する際にリスクを最小化しようとする古典的なポートフォリオ最適化問題です:
\[ \mu^T x = \mu^* \]
変数に対する制約や制限が存在する場合もあれば、存在しない場合もあります。
リサンプリングMV最適化
\[ \frac{1}{m} \left( \sum_{j=1}^{m} \arg\min_{\mu_j^T x = \mu^*} x^T \Sigma_j x \right) \]
リサンプリング平均分散は、線形制約と変数制約のみが存在する場合に使用され、マーコウィッツモデルと類似していますが、期待リターンがランダム変数であると仮定されています。アイデアは、\(m\)個の結果のリターン\(\mu_j\)と共分散\(\Sigma_j\)をシミュレートすることです。これらのシナリオごとにポートフォリオ最適化を実行して最適な保有量を見つけ、その結果を平均化します。このアプローチは、資産の分布に関する事前知識が存在する場合や、過去のデータからの推定が非常に困難な場合に有用です。
期待リターンの最大化
\[ \max_x \mu^T x \]
これは、投資家がリスクやその他の要因を考慮せずに最大のリターンを得ようとする場合です。これらの最適化には注意が必要です。なぜなら、解がリスクに関係なく、少数の資産に重みを置く傾向があるからです。
リスク/コスト回避
\[ \max_x \mu^T x - f(x) \]
コスト回避は、マーコウィッツポートフォリオ最適化の変形です。目標は依然として期待リターンを最大化することですが、ペナルティ項\(f\)で示されるその他の要因を犠牲にします。ペナルティの一般的な形式をいくつか以下に示します:
| \(f(x)\) | 解釈 |
|---|---|
| \(x^T \Sigma x\) | リスク回避 |
| \(c^T \| \bar{x}_i - x_i \|\) | 線形取引コスト |
| \(c_1^T \| \bar{x} - x \| + c_2^T \| \bar{x}_i - x_i \|^2\) | 二次取引コスト |
投資家は上記の形式の組み合わせを選択するか、\(f\)に対して非線形関数を選択することができます。
ここで、\(\bar{x}\)は再配分前のポートフォリオで、\(x\)は新しい配分です。\(\bar{x}_i = x_i\)の場合、\(i\)番目の資産に対して取引(したがってコスト)が発生しないことを意味します。取引コストに対する絶対値関数は最適化ツールにとって問題になる可能性があることに注意してください。このような状況を扱う方法については、セクション5で詳細に説明します。
ブラック・リッターマンモデル
\[ \max_x \left[ x^T \bar{\mu} - \left( \frac{\delta}{2} \right) x^T \bar{\Sigma} x \right] \]
1992年にフィッシャー・ブラックとロバート・リッターマンによって発表されたブラック・リッターマンモデルは、資産の過去のパフォーマンスと将来のパフォーマンスに対する見解を組み合わせています。ブラック・リッターマンの基本的な公式と表記法のレビューを以下に示します。
期待リターンベクトル\(\mu\)の代わりに、均衡リスクプレミアムと市場に対する事前の見解を組み合わせたベクトル\(\bar{\mu}\)を使用します。分布\(\bar{\mu}\)はベイズ分析を使用して計算できます:
\[ \bar{\mu} = \left[ (\tau \Sigma)^{-1} + P' \Omega^{-1} P \right]^{-1} \left[ (\tau \Sigma)^{-1} \Pi + P' \Omega^{-1} Q \right] \]
共分散行列:
\[ \bar{M}^{-1} = \left[ (\tau \Sigma)^{-1} + P' \Omega^{-1} P \right]^{-1} \]
上記の変数は:
- \(\Pi = \delta \Sigma
w_{eq}\):均衡リスクプレミアム
- \(\delta\):リスク回避パラメータ
- \(w_{eq}\):市場ポートフォリオ
- \(\bar{\Sigma} = \Sigma +
\bar{M}^{-1}\):更新された共分散行列
- \(P\):見解行列
- \(Q\):各見解に対するリターン
- \(\tau\):\(Q\)の不確実性
- \(\Omega = diag(P (\tau \Sigma) P^T)\):見解の共分散行列
ブラック・リッターマン最適化を実装するために、投資家は市場に対する見解とそれらに対する信頼区間を形成することから始めます。これらは上記の\(\bar{\mu}\)と\(\bar{\Sigma}\)の式に入力され、最適化に使用されます。リスク回避パラメータ\(\delta\)の選択は、事前のヒューリスティックに基づいています。これは特定の値に設定するか、過去の市場データを使用してキャリブレーションすることができます。
4. nAG最適化
目的関数は、問題と投資家の選好に応じて多くの形をとることができます。最適化問題の目的関数の一般的な形式を以下に示します。
| 目的関数 | 問題タイプ |
|---|---|
| \(c^T x\) | 線形計画法 (LP) |
| \(c^T x + x^T \Sigma x\) | 二次計画法 (QP) |
| \(c^T x + \frac{1}{2} \|b - \Sigma x\|^2\) | 最小二乗法 (LS) |
| \(f(x)\) | 非線形計画法 (NLP) |
NLP問題の場合、凸性が問題になる可能性があることに注意してください。目的関数には多くの局所的な極値が存在する可能性があり、得られた数値解がグローバルな最適解でない可能性があります。
モデルが定式化されたら、最適化ルーチンを選択する時です。表1は、nAGライブラリが扱うことができる問題の種類のいくつかを示し、ルーチンの選択についての推奨を提供しています。
| 目的関数 | ルーチン名 | 制約 | 密/疎 |
|---|---|---|---|
| LP、凸QP、およびLS | nag_opt_lin_lsq_quadratic_dense | 二次 | 密 |
| LPおよびQP | nag_opt_qp_quadratic_dense | 二次 | 密 |
| LPおよび凸QP | nag_opt_sparse_convex_qp | 二次 | 疎 |
| NLP | nag_opt_nlp_nonlinear_dense | 非線形 | 密 |
| NLP | nag_opt_nlp_revcomm | 非線形 | 密 |
| NLP | nag_opt_nlp_sparse | 非線形 | 疎 |
一部の最適化関数は複数のタイプの問題を扱えることに注意してください。例えば、非線形最適化ツールをQP問題に使用することもできますが、計算効率の観点からはそうすべきではありません。
4.1 共分散/相関行列
過去のリターンから共分散行列\(\Sigma\)を計算しようとする際、丸め誤差や不完全なデータにより、計算された行列が非正定値になる可能性があります。問題が十分に制約されていない場合、そのような行列を使用して計算を行うと、奇妙な結果が生じる可能性があります。幸いなことに、多くのnAGアルゴリズムは非正定値行列を検出します。計算された行列が非正定値である場合、nAGライブラリのChapter G02にある最近傍相関行列(NCM)ルーチンが有用かもしれません。これらの関数は、元の計算された行列にある意味で最も近い相関行列を見つけ、重み/因子構造を組み込むことができます。
4.2 フォワードおよびダイレクトコミュニケーション
最適化ルーチンの大部分はフォワードコミュニケーションに基づいています。このようなプログラムでは、ルーチンは結果を得るために一度だけ呼び出され、ユーザーはサブルーチンを通じて必要なすべての情報をnAGルーチンに提供します。しかし、状況によっては、最適化を段階的に行い、新しい情報を得るためにユーザールーチンを繰り返し呼び出す必要があります。
nAGルーチンnag_opt_nlpはフォワードコミュニケーションルーチンで、nag_opt_nlp_revcommはそれに相当するダイレクトコミュニケーションルーチンです。このダイレクトコミュニケーションルーチンは、特に他の言語(例:Microsoft
VBA)から呼び出される場合に有用です。フォワードコミュニケーションアルゴリズムが必要とするコールバック関数のコーディングが面倒な場合があるためです。
4.3 コールドスタートとウォームスタート
コールドスタートは、問題を最初から解くことを指します。しかし、ルーチンが繰り返し呼び出される場合、以前の解から近似解が利用可能です。その場合、次の反復の初期条件を前回の解から提供することができます。このようなウォームスタート機能は、多くのnAG最適化ルーチンで利用可能です。
4.4 目的関数の導関数
nAGは、計算効率のため、特定のアルゴリズムが使用できる限り多くの導関数をユーザーが提供することを推奨しています。特定の目的関数の導関数の計算が困難な場合や、特定の点で導関数が存在しない場合、nAGルーチンは有限差分法を用いて提供された関数の部分微分を自動的に計算します。
有限差分法が計算コストが高すぎたり不正確な場合、あるいは導関数のコーディングが非常に困難な場合、アルゴリズム微分(AD)と呼ばれる別の技術を使用することができます。nAGは、RWTH Aachen大学と密接に協力して、世界中の顧客にADツールとソリューションを提供しています。
4.5 グローバル最適化
目的関数に多くの局所最小値がある場合、グローバル最小値に加えて、そのような問題は局所最適化問題よりもはるかに解くのが困難になる可能性があります。これは、潜在的な最小値がグローバルかどうかを判断するのが難しいためと、局所的な最適解に捕らわれるのを避けるために非局所的な方法が必要になるためです。このような場合、nAGライブラリのChapter E05にあるグローバル最適化メソッドのアルゴリズムを推奨します。
5. 取引コスト
マーコウィッツの古典的な研究では、株式の売買に関連する取引コストは考慮されていません。しかし、ポートフォリオの構築や既存のポートフォリオの再調整において取引コストを組み込むことの重要性は広く認識されています。一般に、取引コストは無視できるほど小さくはなく、最適なポートフォリオは取引の総コストに依存します。資産\(i\)の追加購入をモデル化しましょう:
\[ p_i = \begin{cases} (x_i - \bar{x}_i) & \text{for } x_i > \bar{x}_i \\ 0 & \text{for } x_i \leq \bar{x}_i \end{cases} \]
ここで、\(x_i\)は株式\(i\)の新しいポートフォリオウェイト、\(\bar{x}_i\)は株式\(i\)の元のウェイトです。同様に、資産\(i\)の売却をモデル化します:
\[ q_i = \begin{cases} 0 & \text{for } x_i > \bar{x}_i \\ (\bar{x}_i - x_i) & \text{for } x_i \leq \bar{x}_i \end{cases} \]
\(p_i\)と\(q_i\)の両方が同時に非ゼロになることはないことに注意してください。同じ資産を同時に買うことと売ることを望まないからです。
取引コストのない最小化のための目的関数を\(\phi(x)\)とします。取引コストを含む新しい目的関数は次のようになります:
\[ \phi(x) + \sum_{i=1}^{n} (g_i p_i + h_i q_i) \]
ここで、\(g_i\)と\(h_i\)はそれぞれ資産の購入と売却に関連するコストです。
\(p_i\)と\(q_i\)の両方を追加の(制約付きの)変数として含めることで、問題はスムーズになります。ただし、これにより問題変数の数は2倍になり、\(g_i\)と\(h_i\)が異なる場合は3倍になります。
参考文献
- Becker F, Grtler M and Hibbeln M (2009) Markowitz versus Michaud:
Portfolio Optimization Strategies Reconsidered
- Björk A (1996) Numerical Methods for Least Squares SIAM,
Philadelphia
- Chang T.J, Meade N, Beasley J.E and Sharaiha Y.M (2000) Heuristics
for cardinality constrained portfolio optimization Computers and
Operations Research, to appear
- Dempster A.P, Laired N.M and Rubin D.B (1977) Maximum likelihood
from incomplete data via the EM algorithm (with discussion) Journal of
the Royal Statistical Society, Series B (Methodological), 39, 1-39
- Elton E.J and Gruber M.J (1995) Modern Portfolio Theory and
Investment Analysis Wiley, New York
- Golub G.H and Van Loan C.F (1996) Matrix Computations Johns Hopkins
University Press, Baltimore
- He G and Litterman R The Intuition Behind Black-Litterman Model
Portfolios Available at SSRN
- Lawson C.L and Hanson R.J (1995) Solving Least Squares Problem SIAM,
Philadelphia
- Markowitz H (1952) Portfolio selection Journal of Finance,
7:7791
- Markowitz H, Sharpe W.F and Miller M (1991) Founders of Modern
Finance: Their Prize Winning Concepts and 1990 Nobel Lectures AIMR,
Charlottesville VA
- Markowitz H.M (1987) Mean-Variance Analysis in Portfolio Choice and
Capital Markets Blackwell, Oxford
- Markowitz H.M (1991) Portfolio Selection: Efficient Diversification
of Investments Blackwell, Oxford
- Meucci A (2007) Risk and Asset Allocation Springer, New York
- Meucci A (2010) Quant Nugget 2: Linear vs. Compounded Returns Common
Pitfalls in Portfolio Management GARP Risk Professional
- Michaud R.O (1998) Efficient Asset Management Harvard Business
School Press, Boston
- Moroko W (1998) The Brownian bridge e-m algorithm for covariance
estimation with missing data Journal of Computational Finance,
2:75100
- Naumann U and du Toit J (2014) Adjoint Algorithmic Differentiation
Tool Support for Typical Numerical Patterns in Computational
Finance
- Schmelzer T and Hauser R (2013) Seven Sins in Portfolio
Optimization
- Sharpe W.F (1999) Portfolio Theory and Capital Markets McGraw-Hill,
New York
- Sharpe W.F, Alexander G.J and Bailey J.V (1998) Investments Prentice
Hall, Upper Saddle River, NJ
- Zenios A (1993) Financial Optimization Cambridge University Press, Cambridge
