NAG Library for Python : 利用例

ここでは、NAG Library for Python の利用例をいくつか紹介します。

• 曲面フィッティング
• 大域的最適化
• 分位点回帰
• カーネル密度推定
• 変化点検出

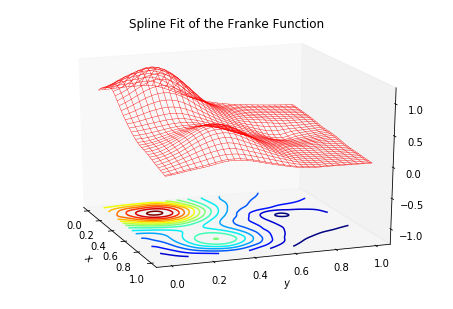
この例では、散布データに曲面をフィットし、結果をプロットします。

まず、適度なサイズの散布 (x, y) データとして、Wichmann-Hill I 乱数生成器を用いて (0, 1] 上の一様乱数を 100 個生成します。

NAG の乱数生成器は、初期化関数によって状態を設定します。
再現可能なシーケンスを生成するには、rand.init_repeat を使用します。
生成器の種類は、引数 genid に指定します。

from naginterfaces.library import rand
statecomm = rand.init_repeat(genid=2, seed=[32958])

乱数生成器を用いて散布 (x, y) データを生成します。

n = 100
x = rand.dist_uniform01(n, statecomm)
y = rand.dist_uniform01(n, statecomm)

散布 (x, y) データに座標 (0, 0) と (1, 1) を含めます。

x[0], y[0] = 0., 0.
x[-1], y[-1] = 1., 1.

Franke 関数（曲面フィッティングのテストによく用いられる関数）から、フィット対象の関数値を得ます。

import numpy as np
f = (
    0.75*np.exp(
        -(
            (9.*x-2.)**2 +
            (9.*y-2.)**2
        )/4.
    ) +
    0.75*np.exp(
        -(9.*x+1.)**2/49. -
        (9.*y+1.)/10.
    ) +
    0.5*np.exp(
        -(
            (9.*x-7.)**2 +
            (9.*y-3.)**2
        )/4.
    ) -
    0.2*np.exp(
        -(9.*x-4.)**2 -
        (9.*y-7.)**2
    )
)

NAG ライブラリは、スムーズな（C¹ または C²）曲面を散布データにフィットさせるための関数 fit.dim2_spline_ts_sctr （Davydov と Zeilfelder の TSFIT パッケージに基づく）を提供します。

まず、関数が使用する三角分割の細かさを設定します。

nxcels = 6
nycels = 6

また、その三角分割のしきい値を設定します。

lsminp = 3
lsmaxp = 100

フィッティング関数は、fit チャプターの初期化・オプション設定関数を用いて通信状態を初期化する必要があります。

from naginterfaces.library import fit
comm = {}
fit.opt_set('Initialize = dim2_spline_ts_sctr', comm)

オプションのデフォルト値を変更したい場合は、オプション設定関数を使います。
ここでは、C² グローバルスムージングを使用し、三角分割の局所近似には平均 Radial Basis Function を使用します。

for fit_opt in [
    'Global Smoothing Level = 2',
    'Averaged Spline = Yes',
    'Local Method = RBF',
]:
    fit.opt_set(fit_opt, comm)

スプライン係数を計算します。
計算結果は通信構造体 comm に入力されます。

fit.dim2_spline_ts_sctr(
    x, y, f, lsminp, lsmaxp, nxcels, nycels, comm,
)

スプラインをプロットするには、評価関数 fit.dim2_spline_ts_evalm を使います。
評価には x 座標のベクトルと y 座標のベクトルが必要です。

x_m = np.linspace(0, 1, 101)
y_m = np.linspace(0, 1, 101)

これらのベクトルによって定義されるグリッド上のスプライン値を計算します。

z_m = fit.dim2_spline_ts_evalm(x_m, y_m, comm)

matplotlib の曲面プロットのために、メッシュベクトルをメッシュグリッドに変換します。

X, Y = np.meshgrid(x_m, y_m, indexing='ij')

スプライン曲面をワイヤーフレームで（等高線と共に）プロットします。

# Jupyter magic for displaying figures inline:
%matplotlib inline

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = plt.figure()
ax = Axes3D(fig)
ax.grid(False)
ax.plot_wireframe(X, Y, z_m, color='red', linewidths=0.4)
ax.contour(X, Y, z_m, 15, offset=-1.2, cmap=cm.jet)
ax.set_title('Spline Fit of the Franke Function')
ax.set_xlabel(r'$\mathit{x}$')
ax.set_ylabel(r'$\mathit{y}$')
ax.set_zlim3d(-1.2, 1.2)
ax.azim = -20
ax.elev = 20
plt.show()

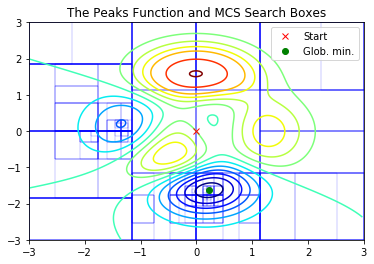
関数の大域的な最大値または最小値を見つけるのは難しい問題です。
制約条件が境界制約のみの問題には、（Huyer と Neumaier の）Multi-level Coordinate Search を使う NAG の最適化ソルバー glopt.bnd_mcs_solve が有効です。

この例では、以下の 2 次元のピーク関数（ソルバーの引数 objfun に適した形式で書かれています）の大域的な最小値を見つけます。

from math import exp
objfun = lambda x, _nstate: (
    3.*(1. - x[0])**2*exp(-x[0]**2 - (x[1] + 1.)**2)
    - (10.*(x[0]/5. - x[0]**3 - x[1]**5)*exp(-x[0]**2 - x[1]**2))
    - 1./3.0*exp(-(x[0] + 1.)**2 - x[1]**2)
)

矩形領域 [-3, -3] × [3, 3] で最小値の探索を行います。

n = 2
bl = [-3.]*n
bu = [3.]*n

引数 ibound = 0 は、境界制約条件がユーザー指定であることをソルバーに伝えます。

ibound = 0

この例では、ソルバーが反復毎に検索する矩形領域をプロットします。
この検索矩形領域は、ソルバー関数のモニタリング・コールバックを用いて取得することができます。

from matplotlib.patches import Rectangle

boxes = []

def monit(
    _ncall, _xbest, _icount, _inlist, _numpts,
    _initpt, _xbaskt, boxl, boxu, _nstate,
):
    boxes.append(Rectangle(boxl, *(boxu - boxl)))

ソルバー関数を呼び出す前に、通信状態を初期化する必要があります。

from naginterfaces.library import glopt
comm = glopt.bnd_mcs_init()

最適化を行います。
モニタリング関数はオプション引数です。

glopt.bnd_mcs_solve(objfun, ibound, bl, bu, comm, monit=monit);

プロットのために目的関数をグリッド化します。

import numpy as np
delta = 0.025
x = np.arange(bl[0], bu[0], delta)
y = np.arange(bl[1], bu[1], delta)
X, Y = np.meshgrid(x, y)
Z = np.empty((len(X), len(Y)))
for i, x_i in enumerate(x):
    for j, y_j in enumerate(y):
        Z[j, i] = objfun([x_i, y_j], None)

プロットに含める最適化の開始点と終了点を格納します。
ソルバー関数のデフォルトのシンプルな初期化メソッド（iinit = 0）では、開始点（initpt）は原点です。

start_x = [0.]*n

この例題の既知の厳密解は (0.23, -1.63) です。

min_x = [0.23, -1.63]

プロットに含める検索矩形領域を集計します。

from matplotlib.collections import PatchCollection
boxes_col = PatchCollection(
    boxes,
    edgecolor='b', facecolor='none', linewidth=0.2,
)

プロットします。

from matplotlib import cm
import matplotlib.pyplot as plt
ax = plt.axes()
ax.contour(
    X, Y, Z,
    levels=[-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 6, 8],
    cmap=cm.jet,
)
ax.plot(start_x[0], start_x[1], 'rx')
ax.plot(min_x[0], min_x[1], 'go')
ax.legend(('Start', 'Glob. min.'), loc='upper right')
ax.add_collection(boxes_col)
ax.axis(xmin=bl[0], ymin=bl[1], xmax=bu[0], ymax=bu[1])
ax.set_title(r'The Peaks Function and MCS Search Boxes')
plt.show()

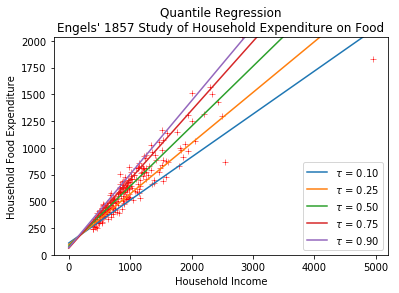
NAG ライブラリ関数 correg.quantile_linreg_easy を用いて、分位点回帰モデルの回帰係数を計算することができます。

この例では、家計の収入（income）が独立変数、それに対して回帰する食費（expenditure）が従属変数です。
このデータは Engels による 1857 年の研究に依ります。

income = [
    420.1577, 541.4117, 901.1575, 639.0802, 750.8756, 945.7989, 829.3979, 979.1648,
    1309.8789, 1492.3987, 502.8390, 616.7168, 790.9225, 555.8786, 713.4412, 838.7561,
    535.0766, 596.4408, 924.5619, 487.7583, 692.6397, 997.8770, 506.9995, 654.1587,
    933.9193, 433.6813, 587.5962, 896.4746, 454.4782, 584.9989, 800.7990, 502.4369,
    713.5197, 906.0006, 880.5969, 796.8289, 854.8791, 1167.3716, 523.8000, 670.7792,
    377.0584, 851.5430, 1121.0937, 625.5179, 805.5377, 558.5812, 884.4005, 1257.4989,
    2051.1789, 1466.3330, 730.0989, 2432.3910, 940.9218, 1177.8547, 1222.5939, 1519.5811,
    687.6638, 953.1192, 953.1192, 953.1192, 939.0418, 1283.4025, 1511.5789, 1342.5821,
    511.7980, 689.7988, 1532.3074, 1056.0808, 387.3195, 387.3195, 410.9987, 499.7510,
    832.7554, 614.9986, 887.4658, 1595.1611, 1807.9520, 541.2006, 1057.6767, 800.7990,
    1245.6964, 1201.0002, 634.4002, 956.2315, 1148.6010, 1768.8236, 2822.5330, 922.3548,
    2293.1920, 627.4726, 889.9809, 1162.2000, 1197.0794, 530.7972, 1142.1526, 1088.0039,
    484.6612, 1536.0201, 678.8974, 671.8802, 690.4683, 860.6948, 873.3095, 894.4598,
    1148.6470, 926.8762, 839.0414, 829.4974, 1264.0043, 1937.9771, 698.8317, 920.4199,
    1897.5711, 891.6824, 889.6784, 1221.4818, 544.5991, 1031.4491, 1462.9497, 830.4353,
    975.0415, 1337.9983, 867.6427, 725.7459, 989.0056, 1525.0005, 672.1960, 923.3977,
    472.3215, 590.7601, 831.7983, 1139.4945, 507.5169, 576.1972, 696.5991, 650.8180,
    949.5802, 497.1193, 570.1674, 724.7306, 408.3399, 638.6713, 1225.7890, 715.3701,
    800.4708, 975.5974, 1613.7565, 608.5019, 958.6634, 835.9426, 1024.8177, 1006.4353,
    726.0000, 494.4174, 776.5958, 415.4407, 581.3599, 643.3571, 2551.6615, 1795.3226,
    1165.7734, 815.6212, 1264.2066, 1095.4056, 447.4479, 1178.9742, 975.8023, 1017.8522,
    423.8798, 558.7767, 943.2487, 1348.3002, 2340.6174, 587.1792, 1540.9741, 1115.8481,
    1044.6843, 1389.7929, 2497.7860, 1585.3809, 1862.0438, 2008.8546, 697.3099, 571.2517,
    598.3465, 461.0977, 977.1107, 883.9849, 718.3594, 543.8971, 1587.3480, 4957.8130,
    969.6838, 419.9980, 561.9990, 689.5988, 1398.5203, 820.8168, 875.1716, 1392.4499,
    1256.3174, 1362.8590, 1999.2552, 1209.4730, 1125.0356, 1827.4010, 1014.1540, 880.3944,
    873.7375, 951.4432, 473.0022, 601.0030, 713.9979, 829.2984, 959.7953, 1212.9613,
    958.8743, 1129.4431, 1943.0419, 539.6388, 463.5990, 562.6400, 736.7584, 1415.4461,
    2208.7897, 636.0009, 759.4010, 1078.8382, 748.6413, 987.6417, 788.0961, 1020.0225,
    1230.9235, 440.5174, 743.0772,
]
expenditure = [
    255.8394, 310.9587, 485.6800, 402.9974, 495.5608, 633.7978, 630.7566,
    700.4409, 830.9586, 815.3602, 338.0014, 412.3613, 520.0006, 452.4015,
    512.7201, 658.8395, 392.5995, 443.5586, 640.1164, 333.8394, 466.9583,
    543.3969, 317.7198, 424.3209, 518.9617, 338.0014, 419.6412, 476.3200,
    386.3602, 423.2783, 503.3572, 354.6389, 497.3182, 588.5195, 654.5971,
    550.7274, 528.3770, 640.4813, 401.3204, 435.9990, 276.5606, 588.3488,
    664.1978, 444.8602, 462.8995, 377.7792, 553.1504, 810.8962, 1067.9541,
    1049.8788, 522.7012, 1424.8047, 517.9196, 830.9586, 925.5795, 1162.0024,
    383.4580, 621.1173, 621.1173, 621.1173, 548.6002, 745.2353, 837.8005,
    795.3402, 418.5976, 508.7974, 883.2780, 742.5276, 242.3202, 242.3202,
    266.0010, 408.4992, 614.7588, 385.3184, 515.6200, 1138.1620, 993.9630,
    299.1993, 750.3202, 572.0807, 907.3969, 811.5776, 427.7975, 649.9985,
    860.6002, 1143.4211, 2032.6792, 590.6183, 1570.3911, 483.4800, 600.4804,
    696.2021, 774.7962, 390.5984, 612.5619, 708.7622, 296.9192, 1071.4627,
    496.5976, 503.3974, 357.6411, 430.3376, 624.6990, 582.5413, 580.2215,
    543.8807, 588.6372, 627.9999, 712.1012, 968.3949, 482.5816, 593.1694,
    1033.5658, 693.6795, 693.6795, 761.2791, 361.3981, 628.4522, 771.4486,
    757.1187, 821.5970, 1022.3202, 679.4407, 538.7491, 679.9981, 977.0033,
    561.2015, 728.3997, 372.3186, 361.5210, 620.8006, 819.9964, 360.8780,
    395.7608, 442.0001, 404.0384, 670.7993, 297.5702, 353.4882, 383.9376,
    284.8008, 431.1000, 801.3518, 448.4513, 577.9111, 570.5210, 865.3205,
    444.5578, 680.4198, 576.2779, 708.4787, 734.2356, 433.0010, 327.4188,
    485.5198, 305.4390, 468.0008, 459.8177, 863.9199, 831.4407, 534.7610,
    392.0502, 934.9752, 813.3081, 263.7100, 769.0838, 630.5863, 645.9874,
    319.5584, 348.4518, 614.5068, 662.0096, 1504.3708, 406.2180, 692.1689,
    588.1371, 511.2609, 700.5600, 1301.1451, 879.0660, 912.8851, 1509.7812,
    484.0605, 399.6703, 444.1001, 248.8101, 527.8014, 500.6313, 436.8107,
    374.7990, 726.3921, 1827.2000, 523.4911, 334.9998, 473.2009, 581.2029,
    929.7540, 591.1974, 637.5483, 674.9509, 776.7589, 959.5170, 1250.9643,
    737.8201, 810.6772, 983.0009, 708.8968, 633.1200, 631.7982, 608.6419,
    300.9999, 377.9984, 397.0015, 588.5195, 681.7616, 807.3603, 696.8011,
    811.1962, 1305.7201, 442.0001, 353.6013, 468.0008, 526.7573, 890.2390,
    1318.8033, 331.0005, 416.4015, 596.8406, 429.0399, 619.6408, 400.7990,
    775.0209, 772.7611, 306.5191, 522.6019,
]

回帰の計画行列では、収入データ列に 1 の列を補うことによって切片項を含めます。

income_X = [[1., incomei] for incomei in income]

分位点を設定します。

tau = [0.10, 0.25, 0.5, 0.75, 0.9]

回帰を計算します。

from naginterfaces.library import correg
regn = correg.quantile_linreg_easy(income_X, expenditure, tau)

回帰係数は、関数の戻りタプル regn の属性 b に返されます。

プロットのために、回帰直線を計算します。

import numpy as np
plot_x = np.linspace(0, max(income))
plot_ys = [regn.b[0, i] + regn.b[1, i]*plot_x for i in range(len(tau))]

収入と食費のデータの散布図に、回帰直線を重ねて描画します。

import matplotlib.pyplot as plt
plt.scatter(income, expenditure, c='red', marker='+', linewidth=0.5)
for tau_i, tau_val in enumerate(tau):
    plt.plot(
        plot_x, plot_ys[tau_i],
        label=r'$\tau$ = {:.2f}'.format(tau_val),
    )

plt.ylim((0., max(expenditure)))
plt.xlabel('Household Income')
plt.ylabel('Household Food Expenditure')
plt.legend(loc='lower right')
plt.title(
    'Quantile Regression\n'
    'Engels\' 1857 Study of Household Expenditure on Food'
)
plt.show()

カーネル密度推定は、観測値から、その観測値が従う（未知の）確率密度関数の値を推定するノンパラメトリックな手法です。
これは、NAG ライブラリ関数 smooth.kerndens_gauss で行うことができます。

この例では、以下のデータを使います。

x = [
    0.114, -0.232, -0.570, 1.853, -0.994, -0.374, -1.028, 0.509, 0.881, -0.453,
    0.588, -0.625, -1.622, -0.567, 0.421, -0.475, 0.054, 0.817, 1.015, 0.608,
    -1.353, -0.912, -1.136, 1.067, 0.121, -0.075, -0.745, 1.217, -1.058, -0.894,
    1.026, -0.967, -1.065, 0.513, 0.969, 0.582, -0.985, 0.097, 0.416, -0.514,
    0.898, -0.154, 0.617, -0.436, -1.212, -1.571, 0.210, -1.101, 1.018, -1.702,
    -2.230, -0.648, -0.350, 0.446, -2.667, 0.094, -0.380, -2.852, -0.888, -1.481,
    -0.359, -0.554, 1.531, 0.052, -1.715, 1.255, -0.540, 0.362, -0.654, -0.272,
    -1.810, 0.269, -1.918, 0.001, 1.240, -0.368, -0.647, -2.282, 0.498, 0.001,
    -3.059, -1.171, 0.566, 0.948, 0.925, 0.825, 0.130, 0.930, 0.523, 0.443,
    -0.649, 0.554, -2.823, 0.158, -1.180, 0.610, 0.877, 0.791, -0.078, 1.412,
]

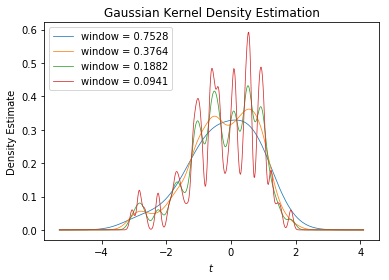
この例では、４つの異なる窓幅で密度推定を繰り返します。

window_ms = [2./2.**i for i in range(4)]

from naginterfaces.library import smooth
comm = {}
k_gs = [smooth.kerndens_gauss(x, comm, window=window_m) for window_m in window_ms]

各戻りタプルの属性 window に使用された窓幅、属性 t に密度推定が計算された点、属性 smooth に推定値が与えれます。

import matplotlib.pyplot as plt
for k_g in k_gs:
    plt.plot(
        k_g.t, k_g.smooth,
        linewidth=0.75, label='window = {:.4f}'.format(k_g.window),
    )

plt.xlabel(r'$\mathit{t}$')
plt.ylabel('Density Estimate')
plt.legend()
plt.title('Gaussian Kernel Density Estimation')
plt.show()

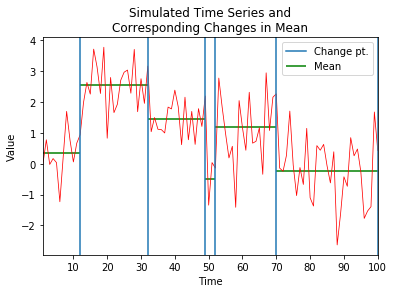
変化点とは、時系列の性質に変化が生じた時点のことです。
NAG ライブラリ関数 tsa.cp_pelt は、単変量時系列の変化点を検出することができます。

この例では、正規分布に従う以下の時系列データを考えます。

y = [
    0., 0.78, -0.02, 0.17, 0.04, -1.23, 0.24, 1.7, 0.77, 0.06,
    0.67, 0.94, 1.99, 2.64, 2.26, 3.72, 3.14, 2.28, 3.78, 0.83,
    2.8, 1.66, 1.93, 2.71, 2.97, 3.04, 2.29, 3.71, 1.69, 2.76,
    1.96, 3.17, 1.04, 1.5, 1.12, 1.11, 1., 1.84, 1.78, 2.39,
    1.85, 0.62, 2.16, 0.78, 1.7, 0.63, 1.79, 1.21, 2.2, -1.34,
    0.04, -0.14, 2.78, 1.83, 0.98, 0.19, 0.57, -1.41, 2.05, 1.17,
    0.44, 2.32, 0.67, 0.73, 1.17, -0.34, 2.95, 1.08, 2.16, 2.27,
    -0.14, -0.24, 0.27, 1.71, -0.04, -1.03, -0.12, -0.67, 1.15,
    -1.1, -1.37, 0.59, 0.44, 0.63, -0.06, -0.62, 0.39, -2.63, -1.63,
    -0.42, -0.73, 0.85, 0.26, 0.48, -0.26, -1.77, -1.53, -1.39, 1.68, 0.43,
]

この例では、平均の変化を調べたいと思いますので、引数 ctype に 1 を設定します。

ctype = 1

また、この問題では分散を 1 と仮定しますので、それを引数 param で NAG 関数に伝えます。

param = [1.]

変化点を検出します。

from naginterfaces.library import tsa
soln = tsa.cp_pelt(ctype, y, param=param)

変化点の位置は、戻りタプル soln の属性 tau に与えれます。
また、推定された確率分布のパラメータは、同じく属性 sparam に与えられます。

時系列と共に、変化点を垂直線でプロットし、対応する平均を水平線でプロットします。

import matplotlib.pyplot as plt
plt.plot(range(1, len(y)+1), y, color='r', linewidth=0.75)
last_cp = 1.
for tau_i, tau_val in enumerate(soln.tau):
    vl = plt.axvline(tau_val, label='Change pt.')
    hl = plt.hlines(
        soln.sparam[2*tau_i],
        xmin=last_cp, xmax=tau_val, color='g', label='Mean',
    )
    last_cp = tau_val

plt.xlim((1, len(y)))
plt.xticks(range(10, len(y)+1, 10))
plt.xlabel('Time')
plt.ylabel('Value')
plt.title(
    'Simulated Time Series and\n'
    'Corresponding Changes in Mean')
plt.legend(handles=[vl, hl], loc='upper right')
plt.show()