誤差の上限とソフトウェア
本セクションでは解の品質に関する情報を応答として返す信頼のおけるソフトウェアの例を示す。最初に自由に使えるソフトウェアパッケージLAPACK
[Anderson et al., 1999]
を見た後、続けて商用ソフトウェアライブラリの例としてnAG
Library [nAG]
を見て行くことにする。本レポートの著者としてはこれら双方のソフトウェア製品に関心を持たざるを得ない。なぜなら彼はLAPACKの開発者の一人であると共に、nAG
Ltd.に所属するソフトウェア開発者でもあるからである。当然のこととして、ここで紹介する例は製品に精通していることとそれらに対する信頼とから選ばれているわけであるが、個人的偏向は避けるように努力する。
LAPACKはLinear Algebra
PACKageの略であり、PC、ワークステーション、高性能共用メモリマシンを対象とした密/帯形状の線形代数問題解法用の数値計算ソフトウェアパッケージである。LAPACKの一つの狙いは移植性を維持しつつ、近年のマシン上で効率良く動作できるようにすることにあった。この目的のためにBLAS(Basic
Linear Algebra
Subprograms)、具体的にはLevel 3
BLASに基づくブロック分割アルゴリズム(block-partitioned
algorithms)を可能な限り幅広く使用している。BLASのインタフェースは共通スカラー/ベクトル用(Level
1)、行列-ベクトル用(Level
2)、行列-行列演算用(Level
3)の3つに区分されている。それらに関する背景と仕様についてはそれぞれ
Lawson et al. [1979], Dongarra et al. [1988a] and Dongarra et al. [1990]
を参照されたい。ブロック分割アルゴリズムに関する情報、及びLAPACKの性能については
Anderson et al. [1999, Chapter 3]
に記載されている。また
Golub and Van Loan [1996, particularly Section 1.3], [Stewart, 1998, Chapter
2]
にも関連する情報が含まれている。
LAPACKには連立1次方程式、線形最小2乗問題、固有値/特異値問題(一般化問題含む)解法用のルーチンの他、行列の因子分解等、基盤要素技術となるルーチンも含まれている。さらに条件と誤差推定に関する面で多くの開発努力が傾注されている。次はLAPACK
Users' Guide 第4章 ---
計算精度と安定性 ---
の先頭パラグラフを引用したものである。
| "これまでより高速のルーチンを提供すると共に、LAPACKはより包括的で改良された誤差の上限値を提供する。我々のゴールはLAPACKで計算されるほとんどすべての量に対して誤差の上限を提示することである。" |
多くの場合、ルーチンは上限値を直接応答として返す。そうでないものに対しては、誤差の上限に関する詳細と、それらを算出するためのコードフラグメントがUsers'
Guideに記載されている。
例えばルーチンDGESVX(Note1)は連立1次方程式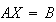 を、partial
pivotingを用いたガウス消去法(Gaussian
elimination)により解く。ここに
を、partial
pivotingを用いたガウス消去法(Gaussian
elimination)により解く。ここに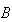 は1つ、あるいは複数の右辺に対応した行列である。インタフェースの一部を記すと次のようになる。
は1つ、あるいは複数の右辺に対応した行列である。インタフェースの一部を記すと次のようになる。
ここに表示された引数により次のような情報を得ることができる。
RCOND |
- | 条件数の逆数である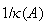 の推定値 の推定値 |
FERR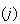 |
- | 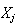 に対する前進誤差推定値 に対する前進誤差推定値 |
BERR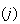 |
- | 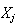 に対するcomponentwiseな相対後退誤差( に対するcomponentwiseな相対後退誤差(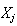 を厳密解にするために必要な を厳密解にするために必要な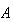 と と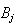 の任意要素に対する最小の相対変動) の任意要素に対する最小の相対変動) |
WORK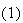 |
- | Pivot成長因子の逆数
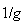 |
INFO |
- | 計算結果の三角因子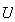 が特異(singular)、または特異に近い場合に正の値を返す が特異(singular)、または特異に近い場合に正の値を返す |
このように数値解の品質を判断する上で必要なすべての情報はDGESVXから提供される。
このルーチンは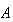 が特異であったり、非常にill-conditionedであったときにオーバフローを回避すべく、
が特異であったり、非常にill-conditionedであったときにオーバフローを回避すべく、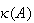 ではなく
ではなく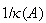 の推定値を応答として返す。引数INFOはLAPACKの警告/エラーフラグであり、ユーザからコール可能なすべてのLAPACKルーチンでサポートされている。正常終了時、その値は
の推定値を応答として返す。引数INFOはLAPACKの警告/エラーフラグであり、ユーザからコール可能なすべてのLAPACKルーチンでサポートされている。正常終了時、その値は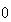 、入力引数に誤りがある場合には負の値となる(例えば
、入力引数に誤りがある場合には負の値となる(例えば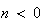 )。しかし異常終了、あるいは上記のように異常終了に近い事態の場合には正の値が返される。上の例において
)。しかし異常終了、あるいは上記のように異常終了に近い事態の場合には正の値が返される。上の例において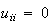 の場合にはINFOは
の場合にはINFOは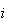 の値を返す。この場合、
の値を返す。この場合、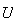 は厳密に特異となるため解は計算されない。
は厳密に特異となるため解は計算されない。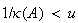 の場合には
の場合には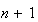 が応答として返される。この場合、
が応答として返される。この場合、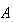 は計算精度において非特異である。後者の場合には解が計算されるが、INFO
は計算精度において非特異である。後者の場合には解が計算されるが、INFO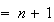 という情報は解が正しい桁を持たない可能性があることを示している。このルーチンは行列
という情報は解が正しい桁を持たない可能性があることを示している。このルーチンは行列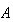 を平衡化させるオプションも有する。ルーチンの詳細についてはUsers'
Guide、あるいはnetlib
(http://www.netlib.org/lapack/index.html)
からダウンロードできるソースコードを参照されたい。
を平衡化させるオプションも有する。ルーチンの詳細についてはUsers'
Guide、あるいはnetlib
(http://www.netlib.org/lapack/index.html)
からダウンロードできるソースコードを参照されたい。
LAPACKからの第2の例としてDGEEVXの例を示す。これは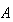 を
を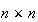 行列としたとき、固有値問題
行列としたとき、固有値問題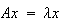 を解き、固有値と固有ベクトル
を解き、固有値と固有ベクトル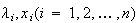 を算出する機能を提供する。行列をバランスさせ、
を算出する機能を提供する。行列をバランスさせ、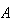 の左固有ベクトルを計算するオプションも用意されている。インタフェースの一部を記すと次のようになる。
の左固有ベクトルを計算するオプションも用意されている。インタフェースの一部を記すと次のようになる。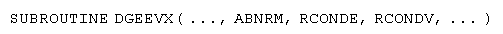
ここに表示された引数により次のような情報を得ることができる。
ABNRM |
- | バランス行列(balanced matrix)のノルム |
RCONDE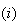 |
- | 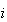 番目の固有値に対する条件数の逆数 番目の固有値に対する条件数の逆数
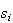 |
RCONDV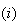 |
- | 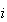 番目の固有ベクトルに対する条件数の逆数
sep 番目の固有ベクトルに対する条件数の逆数
sep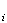 |
算出された固有値、固有ベクトルに対する誤差上限値(近似値)をEERRBD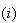 ,
VERRBD
,
VERRBD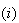 とすると
とすると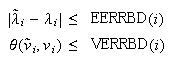 が成り立つ。ここに
が成り立つ。ここに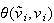 は算出された固有ベクトルと真の固有ベクトル間の偏角とする。これらの上限値を求めるためにはUsers'
Guideに示されている次のようなコードを用意すれば良い。
は算出された固有ベクトルと真の固有ベクトル間の偏角とする。これらの上限値を求めるためにはUsers'
Guideに示されている次のようなコードを用意すれば良い。

これらの上限値は表tab3をベースにしているが、この表はLAPACK
Users' GuideのTable
4.5(非対称固有値問題に対する漸近誤差上限値を与える近似式)から抽出したものである。
| 単一固有値 | 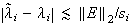 |
| 固有ベクトル | 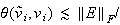 sep sep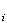 |
表3
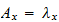 に対する漸近誤差上限値
に対する漸近誤差上限値
この表では固有値が単一固有値(simple
eigenvalues)であることを仮定している。また問題がill-conditionedである場合には、これらの不等式は極端に小さな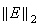 に対してしか成り立たない可能性が出てくる。従ってUsers'
Guideには
に対してしか成り立たない可能性が出てくる。従ってUsers'
Guideには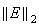 に関する制約があまり強くない大域的誤差上限値を示す表も含まれている。Users'
Guideの表には固有値のクラスタ、及び不変部分空間(invariant
subspaces)に対する不等式も含まれており、これらはDGEEVXではなくDGEESXを使うことによって推定できる。詳細についてはLAPACK
Users' Guide [Anderson et al., 1999, Chapter 4] の他、Golub
and Van Loan [1996, Chapter 7] や Stewart and Sun [1990]
を参照されたい。
に関する制約があまり強くない大域的誤差上限値を示す表も含まれている。Users'
Guideの表には固有値のクラスタ、及び不変部分空間(invariant
subspaces)に対する不等式も含まれており、これらはDGEEVXではなくDGEESXを使うことによって推定できる。詳細についてはLAPACK
Users' Guide [Anderson et al., 1999, Chapter 4] の他、Golub
and Van Loan [1996, Chapter 7] や Stewart and Sun [1990]
を参照されたい。
LAPACKはnetlib(Note2)経由で無償で利用でき、nAG
Fortran 77
Library中にも含まれている他、nAG
Fortran 90 LibraryとC
Library中における密行列用線形代数機能の基盤として使用されている。またnAG
Fortran SMP
Library中にはチューニングの施されたLAPACKルーチンが多数含まれている。MATLABの行列演算もバージョン6以降はLAPACKがベースとなっている
[MathWorks; Higham and Higham, 2000]。
今度はnAG Fortran
Libraryからの例を示す。ルーチンD01AJFは順応型の(adaptive)プロシジャを用いた汎用の積分ルーチンであり、QAGSのQUADPACKルーチンがベースになっている
[Piessens et al.,
1983]。D01AJFは積分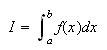 を実行する。ここに
を実行する。ここに![$[a,b]$](graphics/section7__51.png) は有限区間とする。インタフェースの一部を記すと次のようになる。
は有限区間とする。インタフェースの一部を記すと次のようになる。
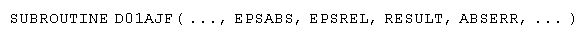
ここに表示された引数により次のような情報を得ることができる。
EPSABS |
- | 必要とされる絶対精度 |
EPSREL |
- | 必要とされる相対精度 |
RESULT |
- | 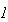 に関し算出された近似値 に関し算出された近似値 |
ABSERR |
- | 絶対誤差の推定値 |
通常の状況下ではABSERRは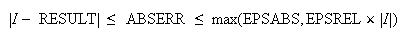 という不等式を満たす。詳細についてはnAG
Libraryマニュアル [nAG,
2003]、及び Piessens et al. [1983]
を参照されたい。QUADPACKはnetlib (Note3)から無償で利用できる。またFortran
90版のQAGSはより新しい設計の数値積分パッケージ
CUBPACK [Cools and Haegemans, 2003]
(これもnetlibから利用可)の中に含まれている。通常、数値積分ルーチンに対する誤差推定は、より細かな刻み(メッシュ)を用いた、あるいはより高次の積分公式を用いた追加の計算時間を必要とする。
という不等式を満たす。詳細についてはnAG
Libraryマニュアル [nAG,
2003]、及び Piessens et al. [1983]
を参照されたい。QUADPACKはnetlib (Note3)から無償で利用できる。またFortran
90版のQAGSはより新しい設計の数値積分パッケージ
CUBPACK [Cools and Haegemans, 2003]
(これもnetlibから利用可)の中に含まれている。通常、数値積分ルーチンに対する誤差推定は、より細かな刻み(メッシュ)を用いた、あるいはより高次の積分公式を用いた追加の計算時間を必要とする。
nAG
Libraryからの2つ目の例としてODEの解法について見てみよう。ルーチンD02PCFは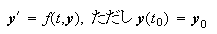 に対し、ルンゲクッタ法によって積分計算を行う。ここに
に対し、ルンゲクッタ法によって積分計算を行う。ここに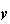 は
は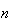 要素からなる解ベクトルであり、
要素からなる解ベクトルであり、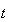 は独立変数である。D02PCFを使用した後でルーチンD02PZFを用いることによって大域的な誤差推定を行うことができる。次はD02PZFに対するインタフェースの一部を示したものである。
は独立変数である。D02PCFを使用した後でルーチンD02PZFを用いることによって大域的な誤差推定を行うことができる。次はD02PZFに対するインタフェースの一部を示したものである。
ここに表示された引数により次のような情報を得ることができる。
RMSERR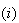 |
- | 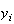 に対するRMS(root
mean square)誤差の近似値 に対するRMS(root
mean square)誤差の近似値 |
ERRMAX |
- | 真の誤差に対する最大近似(maximum approximate true error) |
TERRMX |
- | Maximum approximate true errorが起った最初の点 |
誤差の評価は、元々の解を得るのに使用されたものより高次の手法を用い、より精度の高い解を計算するという代償のもとで行われる。
nAGのD02Pルーチンは Brankin et al. [1992]
によるRKSUITEソフトウェアをベースにしている。このRKSUITEもnetlib(Note4)から利用できる。また
Shampine and Gladwell [1992], Brankin et al. [1993]
についても参照されたい。Fortran
90版のRKSUITEも利用可能である。(Note5) Brankin
and Gladwell [1997]
参照。
nAG Libraryの多くのルーチンが精度に関する情報を返すべく努力している。ルーチンの仕様書には"精度(Accuracy)"と称するセクションが用意されており、さらなる助言や情報が記述されている。例えば最適化ルーチンでは一般的に、それが有効に機能するために満たされなくてはならない最適化条件を記述している。これらのルーチンは慎重であるため、最適点が見出された可能性があっても、すべての最適化条件が満たされているわけではないときには、警告、あるいはエラーを返す場合がある。ユーザの中にはnAGがより楽観的な見方を取るべきと考える方もいるかも知れないが、nAG及びルーチンの設計者たちは信頼性を維持する上でこれが最良のアプローチであると感じている。
