浮動小数とIEEE Arithmetic
浮動小数とは、表現できる数の範囲に不当な制限を加えることなく、計算機の有限語長で表現可能な実数のサブセットを言う。例えば2進浮動演算に対するANSI/IEEE標準
[IEEE, 1985]
では64ビットを用い、概ね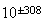 の範囲の倍精度実数が表現される。
の範囲の倍精度実数が表現される。
浮動小数値(floating
point number)
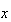 は4つの整数を用いて次のように表現される。
は4つの整数を用いて次のように表現される。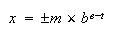 ここに
ここに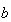 は基数(base,
radix)、
は基数(base,
radix)、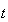 は精度(precision)、
は精度(precision)、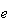 は指数範囲(exponent
range)が
は指数範囲(exponent
range)が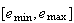 の指数(exponent)、
の指数(exponent)、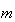 は仮数(mantissa,
significand)と呼ばれる。ただし
は仮数(mantissa,
significand)と呼ばれる。ただし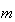 は
は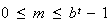 を満足する。
を満足する。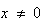 でかつ
でかつ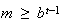 であるとき
であるとき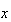 を正規化(normalized)数と言う。
を正規化(normalized)数と言う。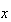 に関する別の等価な表現を記すと次のようになる。
に関する別の等価な表現を記すと次のようになる。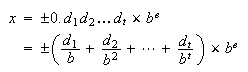 ただし各桁の数は
ただし各桁の数は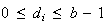 を満たすものとする。
を満たすものとする。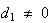 の場合には
の場合には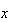 は正規化されていることになる。
は正規化されていることになる。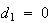 で
で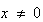 の場合には
の場合には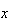 は非正規化(denormalized)数と呼ばれる。
は非正規化(denormalized)数と呼ばれる。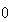 と最小の正規化数の間にある非正規化数をサブノーマル(subnormal)と言う。非正規化数は
と最小の正規化数の間にある非正規化数をサブノーマル(subnormal)と言う。非正規化数は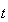 桁の精度を持つわけではない点に注意。
桁の精度を持つわけではない点に注意。
次の例は現実的なものとは言えないがモデルの理解には役に立つ。
Example 2.1 (浮動小数)
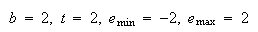
すべての正規化数は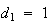 であり、
であり、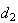 は
は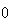 または
または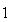 である。すなわち
である。すなわち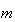 は2進整数
は2進整数
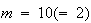 または
または
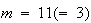 のいずれかである。一方、非正規化数の場合は
のいずれかである。一方、非正規化数の場合は
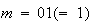 となる。従って最小の正の正規化数は
となる。従って最小の正の正規化数は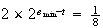 、最大の正規化数は
、最大の正規化数は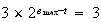 となる。この系において、
となる。この系において、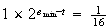 はただ一つの正のサブノーマル数となる。非負の正規化数の全集合は
はただ一つの正のサブノーマル数となる。非負の正規化数の全集合は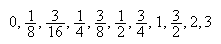 である。非負の浮動小数の集合を図示したものが図1である。ただしサブノーマル数は破線で示されている。
である。非負の浮動小数の集合を図示したものが図1である。ただしサブノーマル数は破線で示されている。
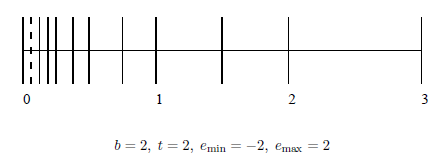
図1 浮動小数の例

浮動小数値は絶対的な意味において等間隔に配置されているわけではないが、相対的な間隔という意味では概ね均一である。今の場合、
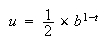
|
(1) |
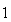 に比べた比率を表す。Example
2.1の場合、
に比べた比率を表す。Example
2.1の場合、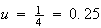 である。実際、
である。実際、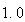 から最も遠い実数は
から最も遠い実数は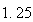 であり、
であり、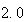 から最も遠い実数は
から最も遠い実数は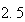 である。この
である。この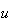 は浮動小数の誤差解析において本質的な意味を持つ。
は浮動小数の誤差解析において本質的な意味を持つ。
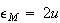 という値はマシン
という値はマシン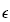 (machine
epsilon)と呼ばれる。
(machine
epsilon)と呼ばれる。
上記ANSI/IEEE標準(通常IEEE演算機能(IEEE
arithmetic)と呼ばれ、もちろん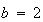 の場合もカバーする)は次の事項に関する仕様を規定する。
の場合もカバーする)は次の事項に関する仕様を規定する。
-
浮動小数の形式
-
基本的浮動小数演算の結果
-
丸めモード(rounding modes)
-
符合付き
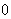 (signed
zero)、無限大(
(signed
zero)、無限大(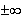 )、非数(NaN:
not-a-number)
)、非数(NaN:
not-a-number)
-
浮動小数例外とその扱い
-
形式間の変換
ありがたいことに近年ではほとんどすべてのマシンがIEEE arithmeticを使用している。この他に基数に依存しない形の一般的なANSI/IEEE標準 [IEEE, 1987] も存在する。表tab1はANSI/IEEEの2進標準を示したものである。
| 形式 | 精度 | 指数部 | 指数範囲 | 近似精度 |
| Single | 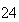 ビット ビット |
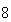 ビット ビット |
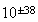 |
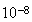 |
| Double | 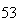 ビット ビット |
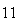 ビット ビット |
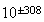 |
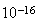 |
| Extended | 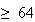 ビット ビット |
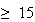 ビット ビット |
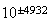 |
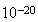 |
表1 IEEE arithmaticの形式
IEEE
arithmeticのデフォルトの丸めモードはround
to
nearestである。この場合、実数はそれに最も近い浮動小数によって代表される(タイの場合の扱い規則については
[Overton, 2001, Chapter 5] を参照)。
ANSI/IEEE標準は浮動小数点演算を標準化する上で大きな助けになるが、それを実装しているマシン間で計算を移し変えた場合に、計算結果が同一になることは保証されない点に注意。コンパイラの最適化、拡張精度レジスタの使用、FMA(fused
multiply-add)といった項目によっては変動が起り得るからである。
浮動小数、IEEE
arithmeticに関するさらなる議論については
Higham [2002] と Overton [2001]
を参照されたい。
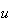 の値はLAPACK関数SLAMCH(単精度演算用)、あるいはDLAMCH(倍精度演算用)から得ることができる(引数CMACHで
の値はLAPACK関数SLAMCH(単精度演算用)、あるいはDLAMCH(倍精度演算用)から得ることができる(引数CMACHで'e'を指定してコールする)。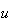 の値はnAG
Fortran Libraryルーチン
X02AJF (Note1)
によっても求めることができる。四捨五入ではなく切捨てを行うマシン上では
の値はnAG
Fortran Libraryルーチン
X02AJF (Note1)
によっても求めることができる。四捨五入ではなく切捨てを行うマシン上では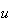 の代りに
の代りに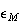 の値が戻されるが、そのようなマシンは稀である。S/DLAMCHにおける
の値が戻されるが、そのようなマシンは稀である。S/DLAMCHにおける'e'とはepsを意味するが、これと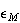 を混同してはならない。Matlabの組込み変数
を混同してはならない。Matlabの組込み変数epsはFortran
95/Fortran
2003の数値問合せ関数
epsilon [Metcalf and Reid, 1996; Metcalf etal., 2004]
と同様、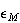 の値を応答する
[MathWorks]。
の値を応答する
[MathWorks]。
