はじめに
このレポートは数学の問題に対する数値解の品質(quality)に関するものである。例えば連立1次方程式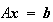
を数値計算用のソフトウェアパッケージを使って解くことを考える。パッケージから得られた解を
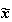としたとき、それが与えられた方程式に対する妥当な解と言えるかどうかを判断したいものとする。残念なことに、ソフトウェアパッケージによる計算結果の精度は十分ではなく、さらには誤ったものであり、しかもユーザには計算結果の品質を判断する手段が何ら与えられないといったことがしばしば起る。1971年にLeslie
Foxは次のようにコメントしている
[Fox, 1971, p. 296]。
| "計算機から出力されてくるすべての結果のうちおよそ80% が、ユーザが信じる以上に誤ったものであるということに対し、私はほとんど疑いを持たない。" |
30年以上経った今でもこの指摘には意味があり一読に値する。これとは別の
Forsythe [1970]
も読みやすい論文である。
数値解の品質とは、計算で得られた解がある適切な尺度においてどの程度良好なものであるかの評価に関係する。品質を意識したソフトウェアは信頼の置けるアルゴリズムを実装すると共に、可能であれば解品質の尺度を提供すべきである。
本レポートにおいては数値解の品質を理解し計測する上で重要な概念について紹介する。特に条件、安定性、誤差解析の考え方、及びそれらが数値計算ソフトウェアの中でどう実現されているかについて見て行くことにする。ここではLAPACK
[Anderson et al., 1999] ---
密(dense)、及び帯状の(banded)線形代数問題解法用パッケージ
---
を主要な例として取り上げるが、nAG
Library [nAG]
等からの例についても議論の対象とする。目的とするところは誤差解析をどのように行うかを示すことではなく、上記の概念を理解することが数値解の品質を判断する上でなぜ重要なのかを示すと共に、結果品質の指標を応答として返すソフトウェアの使用を奨励することにある。信頼できる数値計算ソフトウェアを設計する際に重要となるいくつかの概念を簡単な例を用いて説明する。
計算機は数値計算に浮動小数演算を用いるので、まず浮動小数についての説明から始めることにする。