概要
本サンプルはFortran言語によりLAPACKルーチンZHEGVを利用するサンプルプログラムです。
一般化エルミート固有値問題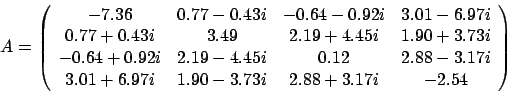
及び
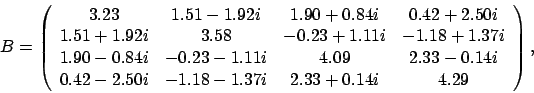
ZHEGVDの例題プログラムは一般化エルミート固有値問題 ![]() の解き方を示します。
の解き方を示します。
入力データ
(本ルーチンの詳細はZHEGV のマニュアルページを参照)| このデータをダウンロード |
ZHEGV Example Program Data
4 :Value of N
(-7.36, 0.00) ( 0.77, -0.43) (-0.64, -0.92) ( 3.01, -6.97)
( 3.49, 0.00) ( 2.19, 4.45) ( 1.90, 3.73)
( 0.12, 0.00) ( 2.88, -3.17)
(-2.54, 0.00) :End of matrix A
( 3.23, 0.00) ( 1.51, -1.92) ( 1.90, 0.84) ( 0.42, 2.50)
( 3.58, 0.00) (-0.23, 1.11) (-1.18, 1.37)
( 4.09, 0.00) ( 2.33, -0.14)
( 4.29, 0.00) :End of matrix B
出力結果
(本ルーチンの詳細はZHEGV のマニュアルページを参照)| この出力例をダウンロード |
ZHEGV Example Program Results
Eigenvalues
-5.9990 -2.9936 0.5047 3.9990
Eigenvectors
1 2 3 4
1 1.7405 -0.6626 0.2835 1.2378
0.0000 0.2258 -0.5806 0.0000
2 -0.4136 -0.1164 -0.3769 -0.5608
-0.4689 -0.0178 -0.3194 -0.3729
3 -0.8404 0.9098 -0.3338 -0.6643
-0.2483 0.0000 -0.0134 -0.1021
4 0.3021 -0.6120 0.6663 0.1589
0.6103 -0.5348 0.0000 0.8366
Estimate of reciprocal condition number for B
2.5E-03
Error estimates for the eigenvalues
6.7E-13 4.1E-13 1.9E-13 5.0E-13
Error estimates for the eigenvectors
1.2E-12 1.1E-12 8.5E-13 9.4E-13
ソースコード
(本ルーチンの詳細はZHEGV のマニュアルページを参照)※本サンプルソースコードのご利用手順は「サンプルのコンパイル及び実行方法」をご参照下さい。
| このソースコードをダウンロード |
Program zhegv_example
! ZHEGV Example Program Text
! Copyright 2017, Numerical Algorithms Group Ltd. http://www.nag.com
! .. Use Statements ..
Use lapack_example_aux, Only: nagf_file_print_matrix_complex_gen
Use lapack_interfaces, Only: ddisna, zhegv, zlanhe, ztrcon
Use lapack_precision, Only: dp
! .. Implicit None Statement ..
Implicit None
! .. Parameters ..
Integer, Parameter :: nb = 64, nin = 5, nout = 6
! .. Local Scalars ..
Complex (Kind=dp) :: scal
Real (Kind=dp) :: anorm, bnorm, eps, rcond, rcondb, t1, t2, t3
Integer :: i, ifail, info, k, lda, ldb, lwork, n
! .. Local Arrays ..
Complex (Kind=dp), Allocatable :: a(:, :), b(:, :), work(:)
Complex (Kind=dp) :: dummy(1)
Real (Kind=dp), Allocatable :: eerbnd(:), rcondz(:), rwork(:), w(:), &
zerbnd(:)
! .. Intrinsic Procedures ..
Intrinsic :: abs, conjg, epsilon, max, maxloc, nint, real
! .. Executable Statements ..
Write (nout, *) 'ZHEGV Example Program Results'
Write (nout, *)
! Skip heading in data file
Read (nin, *)
Read (nin, *) n
lda = n
ldb = n
Allocate (a(lda,n), b(ldb,n), eerbnd(n), rcondz(n), rwork(3*n-2), w(n), &
zerbnd(n))
! Use routine workspace query to get optimal workspace.
lwork = -1
Call zhegv(1, 'Vectors', 'Upper', n, a, lda, b, ldb, w, dummy, lwork, &
rwork, info)
! Make sure that there is enough workspace for block size nb.
lwork = max((nb+1)*n, nint(real(dummy(1))))
Allocate (work(lwork))
! Read the upper triangular parts of the matrices A and B
Read (nin, *)(a(i,i:n), i=1, n)
Read (nin, *)(b(i,i:n), i=1, n)
! Compute the one-norms of the symmetric matrices A and B
anorm = zlanhe('One norm', 'Upper', n, a, lda, rwork)
bnorm = zlanhe('One norm', 'Upper', n, b, ldb, rwork)
! Solve the generalized Hermitian eigenvalue problem
! A*x = lambda*B*x (itype = 1)
Call zhegv(1, 'Vectors', 'Upper', n, a, lda, b, ldb, w, work, lwork, &
rwork, info)
If (info==0) Then
! Print solution
Write (nout, *) 'Eigenvalues'
Write (nout, 100) w(1:n)
Flush (nout)
! Normalize the eigenvectors, largest element real
! (normalization w.r.t B unaffected: Z^HBZ = I).
Do i = 1, n
rwork(1:n) = abs(a(1:n,i))
k = maxloc(rwork(1:n), 1)
scal = conjg(a(k,i))/abs(a(k,i))
a(1:n, i) = a(1:n, i)*scal
End Do
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
Call nagf_file_print_matrix_complex_gen('General', ' ', n, n, a, lda, &
'Eigenvectors', ifail)
! Call ZTRCON to estimate the reciprocal condition
! number of the Cholesky factor of B. Note that:
! cond(B) = 1/rcond**2
Call ztrcon('One norm', 'Upper', 'Non-unit', n, b, ldb, rcond, work, &
rwork, info)
! Print the reciprocal condition number of B
rcondb = rcond**2
Write (nout, *)
Write (nout, *) 'Estimate of reciprocal condition number for B'
Write (nout, 110) rcondb
Flush (nout)
! Get the machine precision, eps, and if rcondb is not less
! than eps**2, compute error estimates for the eigenvalues and
! eigenvectors
eps = epsilon(1.0E0_dp)
If (rcond>=eps) Then
! Call DDISNA to estimate reciprocal condition
! numbers for the eigenvectors of (A - lambda*B)
Call ddisna('Eigenvectors', n, n, w, rcondz, info)
! Compute the error estimates for the eigenvalues and
! eigenvectors
t1 = eps/rcondb
t2 = anorm/bnorm
t3 = t2/rcond
Do i = 1, n
eerbnd(i) = t1*(t2+abs(w(i)))
zerbnd(i) = t1*(t3+abs(w(i)))/rcondz(i)
End Do
! Print the approximate error bounds for the eigenvalues
! and vectors
Write (nout, *)
Write (nout, *) 'Error estimates for the eigenvalues'
Write (nout, 110) eerbnd(1:n)
Write (nout, *)
Write (nout, *) 'Error estimates for the eigenvectors'
Write (nout, 110) zerbnd(1:n)
Else
Write (nout, *)
Write (nout, *) 'B is very ill-conditioned, error ', &
'estimates have not been computed'
End If
Else If (info>n) Then
i = info - n
Write (nout, 120) 'The leading minor of order ', i, &
' of B is not positive definite'
Else
Write (nout, 130) 'Failure in ZHEGV. INFO =', info
End If
100 Format (3X, (6F11.4))
110 Format (4X, 1P, 6E11.1)
120 Format (1X, A, I4, A)
130 Format (1X, A, I4)
End Program
