ZGBSVX(複素線形方程式) LAPACKサンプルソースコード

概要

本サンプルはFortran言語によりLAPACKルーチンZGBSVXを利用するサンプルプログラムです。

以下の式を解きます。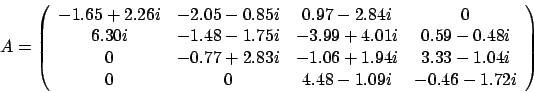

$\begin{displaymath} A X = B, \end{displaymath}$

は帯行列です。

$\begin{displaymath} A = \left( \begin{array}{cccc} -1.65 + 2.26 i & -2.05 - 0... ... 0 & 0 & 4.48 - 1.09 i & -0.46 - 1.72 i \end{array} \right) \end{displaymath}$

及び

$\begin{displaymath} B = \left( \begin{array}{cc} -1.06 + 21.50 i & 12.85 + 2.... ... \\ -34.56 + 16.73 i & 26.01 + 31.97 i \end{array} \right). \end{displaymath}$

後方エラーと前方エラーの推定値、条件数、軸要素成長乗数、及び

の均衡化についてが合わせて出力されます。

入力データ

（本ルーチンの詳細はZGBSVX のマニュアルページを参照）

このデータをダウンロード

ZGBSVX Example Program Data
  4  2  1  2                                       :Values of N, NRHS, KL and KU
 (-1.65, 2.26) (-2.05,-0.85) ( 0.97,-2.84)
 ( 0.00, 6.30) (-1.48,-1.75) (-3.99, 4.01) ( 0.59,-0.48)
               (-0.77, 2.83) (-1.06, 1.94) ( 3.33,-1.04)
                             ( 4.48,-1.09) (-0.46,-1.72)  :End of matrix A
 ( -1.06, 21.50) ( 12.85,  2.84)
 (-22.72,-53.90) (-70.22, 21.57)
 ( 28.24,-38.60) (-20.73, -1.23)
 (-34.56, 16.73) ( 26.01, 31.97)                          :End of matrix B

出力結果

（本ルーチンの詳細はZGBSVX のマニュアルページを参照）

この出力例をダウンロード

 ZGBSVX Example Program Results

 Solution(s)
                    1                 2
 1  (-3.0000, 2.0000) ( 1.0000, 6.0000)
 2  ( 1.0000,-7.0000) (-7.0000,-4.0000)
 3  (-5.0000, 4.0000) ( 3.0000, 5.0000)
 4  ( 6.0000,-8.0000) (-8.0000, 2.0000)

 Backward errors (machine-dependent)
       1.8E-17    5.1E-17

 Estimated forward error bounds (machine-dependent)
       3.5E-14    4.3E-14

 Estimate of reciprocal condition number
       9.6E-03

 A has not been equilibrated

 Estimate of reciprocal pivot growth factor
       1.0E+00

ソースコード

（本ルーチンの詳細はZGBSVX のマニュアルページを参照）

※本サンプルソースコードのご利用手順は「サンプルのコンパイル及び実行方法」をご参照下さい。

このソースコードをダウンロード

    Program zgbsvx_example

!     ZGBSVX Example Program Text

!     Copyright 2017, Numerical Algorithms Group Ltd. http://www.nag.com

!     .. Use Statements ..
      Use lapack_example_aux, Only: nagf_file_print_matrix_complex_gen_comp
      Use lapack_interfaces, Only: zgbsvx
      Use lapack_precision, Only: dp
!     .. Implicit None Statement ..
      Implicit None
!     .. Parameters ..
      Integer, Parameter :: nin = 5, nout = 6
!     .. Local Scalars ..
      Real (Kind=dp) :: rcond
      Integer :: i, ifail, info, j, k, kl, ku, ldab, ldafb, ldb, ldx, n, nrhs
      Character (1) :: equed
!     .. Local Arrays ..
      Complex (Kind=dp), Allocatable :: ab(:, :), afb(:, :), b(:, :), work(:), &
        x(:, :)
      Real (Kind=dp), Allocatable :: berr(:), c(:), ferr(:), r(:), rwork(:)
      Integer, Allocatable :: ipiv(:)
      Character (1) :: clabs(1), rlabs(1)
!     .. Intrinsic Procedures ..
      Intrinsic :: max, min
!     .. Executable Statements ..
      Write (nout, *) 'ZGBSVX Example Program Results'
      Write (nout, *)
      Flush (nout)
!     Skip heading in data file
      Read (nin, *)
      Read (nin, *) n, nrhs, kl, ku
      ldb = n
      ldx = n
      ldab = kl + ku + 1
      ldafb = ldab + kl
      Allocate (ab(ldab,n), afb(ldafb,n), b(ldb,nrhs), work(2*n), x(ldx,nrhs), &
        berr(nrhs), c(n), ferr(nrhs), r(n), rwork(n), ipiv(n))

!     Read the band matrix A and B from data file

      k = ku + 1
      Read (nin, *)((ab(k+i-j,j),j=max(i-kl,1),min(i+ku,n)), i=1, n)
      Read (nin, *)(b(i,1:nrhs), i=1, n)

!     Solve the equations AX = B for X

      Call zgbsvx('Equilibration', 'No transpose', n, kl, ku, nrhs, ab, ldab, &
        afb, ldafb, ipiv, equed, r, c, b, ldb, x, ldx, rcond, ferr, berr, &
        work, rwork, info)

      If ((info==0) .Or. (info==n+1)) Then

!       Print solution, error bounds, condition number, the form
!       of equilibration and the pivot growth factor

!       ifail: behaviour on error exit
!              =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
        ifail = 0
        Call nagf_file_print_matrix_complex_gen_comp('General', ' ', n, nrhs, &
          x, ldx, 'Bracketed', 'F7.4', 'Solution(s)', 'Integer', rlabs, &
          'Integer', clabs, 80, 0, ifail)

        Write (nout, *)
        Write (nout, *) 'Backward errors (machine-dependent)'
        Write (nout, 100) berr(1:nrhs)
        Write (nout, *)
        Write (nout, *) 'Estimated forward error bounds (machine-dependent)'
        Write (nout, 100) ferr(1:nrhs)
        Write (nout, *)
        Write (nout, *) 'Estimate of reciprocal condition number'
        Write (nout, 100) rcond
        Write (nout, *)
        If (equed=='N') Then
          Write (nout, *) 'A has not been equilibrated'
        Else If (equed=='R') Then
          Write (nout, *) 'A has been row scaled as diag(R)*A'
        Else If (equed=='C') Then
          Write (nout, *) 'A has been column scaled as A*diag(C)'
        Else If (equed=='B') Then
          Write (nout, *) &
            'A has been row and column scaled as diag(R)*A*diag(C)'
        End If
        Write (nout, *)
        Write (nout, *) 'Estimate of reciprocal pivot growth factor'
        Write (nout, 100) rwork(1)

        If (info==n+1) Then
          Write (nout, *)
          Write (nout, *) 'The matrix A is singular to working precision'
        End If
      Else
        Write (nout, 110) 'The (', info, ',', info, ')', &
          ' element of the factor U is zero'
      End If

100   Format ((3X,1P,7E11.1))
110   Format (1X, A, I3, A, I3, A, A)
    End Program

ご案内

複素線形方程式: 帯行列 : (右辺は行列)

LAPACKサンプルソースコード : 使用ルーチン名：ZGBSVX

概要

入力データ

出力結果

ソースコード