概要
本サンプルはFortran言語によりLAPACKルーチンDGGESを利用するサンプルプログラムです。
行列対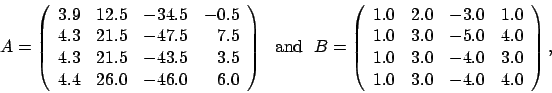
ここで
入力データ
(本ルーチンの詳細はDGGES のマニュアルページを参照)| このデータをダウンロード |
DGGES Example Program Data 4 :Value of N 3.9 12.5 -34.5 -0.5 4.3 21.5 -47.5 7.5 4.3 21.5 -43.5 3.5 4.4 26.0 -46.0 6.0 :End of matrix A 1.0 2.0 -3.0 1.0 1.0 3.0 -5.0 4.0 1.0 3.0 -4.0 3.0 1.0 3.0 -4.0 4.0 :End of matrix B
出力結果
(本ルーチンの詳細はDGGES のマニュアルページを参照)| この出力例をダウンロード |
DGGES Example Program Results
Matrix A
1 2 3 4
1 3.9000 12.5000 -34.5000 -0.5000
2 4.3000 21.5000 -47.5000 7.5000
3 4.3000 21.5000 -43.5000 3.5000
4 4.4000 26.0000 -46.0000 6.0000
Matrix B
1 2 3 4
1 1.0000 2.0000 -3.0000 1.0000
2 1.0000 3.0000 -5.0000 4.0000
3 1.0000 3.0000 -4.0000 3.0000
4 1.0000 3.0000 -4.0000 4.0000
Warning: Floating underflow occurred
Number of eigenvalues for which SELCTG is true = 2
(dimension of deflating subspaces)
Selected generalized eigenvalues
1 ( 2.000, 0.000)
2 ( 4.000, 0.000)
ソースコード
(本ルーチンの詳細はDGGES のマニュアルページを参照)※本サンプルソースコードのご利用手順は「サンプルのコンパイル及び実行方法」をご参照下さい。
| このソースコードをダウンロード |
! DGGES Example Program Text
! Copyright 2017, Numerical Algorithms Group Ltd. http://www.nag.com
Module dgges_mod
! DGGES Example Program Module:
! Parameters and User-defined Routines
! .. Use Statements ..
Use lapack_precision, Only: dp
! .. Implicit None Statement ..
Implicit None
! .. Accessibility Statements ..
Private
Public :: selctg
! .. Parameters ..
Integer, Parameter, Public :: nb = 64, nin = 5, nout = 6
Contains
Function selctg(ar, ai, b)
! Logical function selctg for use with DGGES (DGGES)
! Returns the value .TRUE. if the eigenvalue is real and positive
! .. Function Return Value ..
Logical :: selctg
! .. Scalar Arguments ..
Real (Kind=dp), Intent (In) :: ai, ar, b
! .. Executable Statements ..
selctg = (ar>0._dp .And. ai==0._dp .And. b/=0._dp)
Return
End Function
End Module
Program dgges_example
! DGGES Example Main Program
! .. Use Statements ..
Use blas_interfaces, Only: dgemm
Use dgges_mod, Only: nb, nin, nout, selctg
Use lapack_example_aux, Only: nagf_file_print_matrix_real_gen
Use lapack_interfaces, Only: dgges, dlange
Use lapack_precision, Only: dp
! .. Implicit None Statement ..
Implicit None
! .. Local Scalars ..
Real (Kind=dp) :: alph, bet, normd, norme
Integer :: i, ifail, info, lda, ldb, ldc, ldd, lde, ldvsl, ldvsr, lwork, &
n, sdim
! .. Local Arrays ..
Real (Kind=dp), Allocatable :: a(:, :), alphai(:), alphar(:), b(:, :), &
beta(:), c(:, :), d(:, :), e(:, :), vsl(:, :), vsr(:, :), work(:)
Real (Kind=dp) :: dummy(1)
Logical, Allocatable :: bwork(:)
! .. Intrinsic Procedures ..
Intrinsic :: epsilon, max, nint
! .. Executable Statements ..
Write (nout, *) 'DGGES Example Program Results'
Write (nout, *)
Flush (nout)
! Skip heading in data file
Read (nin, *)
Read (nin, *) n
lda = n
ldb = n
ldc = n
ldd = n
lde = n
ldvsl = n
ldvsr = n
Allocate (a(lda,n), alphai(n), alphar(n), b(ldb,n), beta(n), &
vsl(ldvsl,n), vsr(ldvsr,n), bwork(n), c(ldc,n), d(ldd,n), e(lde,n))
! Use routine workspace query to get optimal workspace.
lwork = -1
Call dgges('Vectors (left)', 'Vectors (right)', 'Sort', selctg, n, a, &
lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, &
dummy, lwork, bwork, info)
! Make sure that there is enough workspace for block size nb.
lwork = max(8*n+16+n*nb, nint(dummy(1)))
Allocate (work(lwork))
! Read in the matrices A and B
Read (nin, *)(a(i,1:n), i=1, n)
Read (nin, *)(b(i,1:n), i=1, n)
! Copy A and B into D and E respectively
d(1:n, 1:n) = a(1:n, 1:n)
e(1:n, 1:n) = b(1:n, 1:n)
! Print matrices A and B
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
Call nagf_file_print_matrix_real_gen('General', ' ', n, n, a, lda, &
'Matrix A', ifail)
Write (nout, *)
Flush (nout)
ifail = 0
Call nagf_file_print_matrix_real_gen('General', ' ', n, n, b, ldb, &
'Matrix B', ifail)
Write (nout, *)
Flush (nout)
! Find the generalized Schur form
Call dgges('Vectors (left)', 'Vectors (right)', 'Sort', selctg, n, a, &
lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, work, &
lwork, bwork, info)
If (info==0 .Or. info==(n+2)) Then
! Compute A - Q*S*Z^T from the factorization of (A,B) and store in
! matrix D
alph = 1.0_dp
bet = 0.0_dp
Call dgemm('N', 'N', n, n, n, alph, vsl, ldvsl, a, lda, bet, c, ldc)
alph = -1.0_dp
bet = 1.0_dp
Call dgemm('N', 'T', n, n, n, alph, c, ldc, vsr, ldvsr, bet, d, ldd)
! Compute B - Q*T*Z^T from the factorization of (A,B) and store in
! matrix E
alph = 1.0_dp
bet = 0.0_dp
Call dgemm('N', 'N', n, n, n, alph, vsl, ldvsl, b, ldb, bet, c, ldc)
alph = -1.0_dp
bet = 1.0_dp
Call dgemm('N', 'T', n, n, n, alph, c, ldc, vsr, ldvsr, bet, e, lde)
! Find norms of matrices D and E and warn if either is too large
normd = dlange('O', ldd, n, d, ldd, work)
norme = dlange('O', lde, n, e, lde, work)
If (normd>epsilon(1.0E0_dp)**0.8_dp .Or. norme>epsilon(1.0E0_dp)** &
0.8_dp) Then
Write (nout, *) 'Norm of A-(Q*S*Z^T) or norm of B-(Q*T*Z^T) &
&is much greater than 0.'
Write (nout, *) 'Schur factorization has failed.'
Else
! Print solution
Write (nout, 100) &
'Number of eigenvalues for which SELCTG is true = ', sdim, &
'(dimension of deflating subspaces)'
Write (nout, *)
! Print generalized eigenvalues
Write (nout, *) 'Selected generalized eigenvalues'
Do i = 1, sdim
If (beta(i)/=0.0_dp) Then
Write (nout, 120) i, '(', alphar(i)/beta(i), ',', &
alphai(i)/beta(i), ')'
Else
Write (nout, 130) i
End If
End Do
Write (nout, *)
If (info==(n+2)) Then
Write (nout, 140) '***Note that rounding errors mean ', &
'that leading eigenvalues in the generalized', &
'Schur form no longer satisfy SELCTG = .TRUE.'
Write (nout, *)
End If
End If
Else
Write (nout, 110) 'Failure in DGGES. INFO =', info
End If
100 Format (1X, A, I4, /, 1X, A)
110 Format (1X, A, I4)
120 Format (1X, I4, 5X, A, F7.3, A, F7.3, A)
130 Format (1X, I4, 'Eigenvalue is infinite')
140 Format (1X, 2A, /, 1X, A)
End Program
