はじめに
本プロジェクトでは、Fortranを用いて時系列データに対する機械学習モデルを構築し、気温予測モデルを構築しました。具体的には、過去24時間の連続した毎時気温データと日時情報のみを用いて、今後1時間から12時間先までの気温を予測するモデルを開発しました。
このモデルの特徴は以下の通りです:
- 入力:過去24時間の連続した毎時気温データと日時情報
- 出力:1時間後から12時間後までの各時間の予測気温
- 手法:リッジ回帰を用いた時系列予測
また、モデル構築の過程で以下の概念を適用しました:
- 特徴量エンジニアリングと変数選択
- 多重共線性の評価と対処
- リッジ回帰による正則化
- モデルの性能評価と解釈
データセットと特徴量エンジニアリング
データセット
使用したデータは気象庁から入手した東京の毎時気温データです。
- 学習データ:2021年1月1日 00:00 から 2022年12月31日 23:00 まで(17,520データポイント)
- 検証データ:2023年1月1日 00:00 から 2023年12月31日 23:00 まで(8,760データポイント)
データの例:
年月日時,気温(℃),気温(℃),気温(℃)
,,品質情報,均質番号
2021/1/1 0:00:00,1.1,8,1
2021/1/1 1:00:00,0.8,8,1
2021/1/1 2:00:00,0.4,8,1
...特徴量エンジニアリング
モデルの入力として、過去24時間分の温度データと日時情報(月、日、時)のみを用いて、以下の10の特徴量を設計しました。これらの特徴量は全て、与えられた限られた情報から算出可能です:
- 1時間前の気温:\(X_1 = T_{t-1}\)
- 時間の周期性(sin):\(X_2 = \sin(2\pi h / 24)\), \(h\)は時間(0-23)
- 時間の周期性(cos):\(X_3 = \cos(2\pi h / 24)\)
- 12時間移動平均温度:\(X_4 = \frac{1}{12}\sum_{i=1}^{12} T_{t-i}\)
- 日内温度範囲:\(X_5 = \max(T_{t-23}, ..., T_t) - \min(T_{t-23}, ..., T_t)\)
- 24時間前との温度差:\(X_6 = T_t - T_{t-24}\)
- 温度の加速度:\(X_7 = (T_t - T_{t-1}) - (T_{t-1} - T_{t-2})\)
- 年間の季節変動(sin):\(X_8 = \sin(2\pi d / 365)\), \(d\)は年間の日数(1-365)
- 年間の季節変動(cos):\(X_9 = \cos(2\pi d / 365)\)
- 過去12時間の温度の標準偏差:\(X_{10} = \sqrt{\frac{1}{11}\sum_{i=1}^{12} (T_{t-i} - \bar{T})^2}\), \(\bar{T}\)は過去12時間の平均気温
変数選択プロセス
当初は20以上の特徴量を検討しましたが、以下のプロセスを経て最終的に10の特徴量に絞り込みました:
VIF分析: g02kafルーチンの出力結果を用いてVIF(分散拡大要因)を計算し、多重共線性を評価しました。VIF > 10の特徴量を潜在的な問題として特定しました。
このプロセスを通じて、例えば以下のような決定を行いました:
- 移動平均: 3時間、6時間、12時間の移動平均を検討しましたが、VIF分析の結果、12時間移動平均のみを採用しました。
- 季節性: 月単位と日単位の周期性を比較し、より細かな変動を捉えられる日単位の周期性を採用しました。
これらの選択により、モデルの複雑さを抑えつつ、予測精度を維持することができました。
モデルの実装
Fortranの選択理由
本プロジェクトでは、以下の理由からFortranを選択しました:
- 高速な数値計算能力:気象データのような大規模な数値計算に適しています。
- 科学技術計算での実績:気象モデルなど、多くの科学技術計算で広く使用されています。
リッジ回帰の採用理由
リッジ回帰を採用した主な理由は以下の通りです:
- 多重共線性への対処:気温データの特徴量間に存在する可能性のある多重共線性の問題を緩和できる
- 過学習の抑制:L2正則化によりモデルの過学習の抑制と汎化性能を向上できる
- 解釈可能性:線形モデルであるため、各特徴量の影響を解釈しやすい
実装の詳細
モデルの実装には、nAG(Numerical Algorithms Group)ライブラリのg02kafルーチンを利用しました。g02kafは、リッジ回帰を計算し、4つの予測誤差基準のいずれかを使用してリッジパラメータを最適化するルーチンです。このルーチンは多重共線性を抑え、モデルの一般化性能を向上させるためにパラメータを正則化します。
データの読み込みと前処理
- 気象庁のCSVファイルから日時と気温データを読み込み
- 欠損値や異常値のチェックと処理
特徴量の計算
- 上記で定義した10の特徴量を各時点で計算
データの標準化
- 各特徴量について、平均と標準偏差を計算
- \(X_{standardized} = \frac{X - \mu}{\sigma}\)
リッジ回帰モデルの構築
- 1時間後から12時間後まで、各予測時間ごとに合計12個のモデルを構築
- nAG g02kafルーチンを使用してリッジパラメータを最適化
モデルの評価
- 訓練データと検証データそれぞれで予測を行い、評価指標を計算
nAG g02kafルーチンでは、リッジ回帰のパラメータ最適化にベイズ情報量基準(BIC)を使うオプションを指定しました:
opt = 4 ! BICを使用して最適なリッジパラメータを選択これらの設定により、過学習を抑制しつつ、予測精度が良いモデルを構築することができました。
結果と評価
各予測時間(1時間後から12時間後まで)のモデルについて、以下の評価指標を計算しました:
- R-squared(決定係数)
- RMSE(平均二乗誤差の平方根)
- MAE(平均絶対誤差)
また、各特徴量のVIF(分散拡大要因)も確認し、多重共線性の評価に使用しました。
以下は1時間後予測モデルの詳細な結果例です。この出力には、モデルのパラメータ、性能指標、係数、そしてVIF(分散拡大要因)が含まれています:
Model for 1 hour(s) forecast:
Ridge parameter (h): 0.000009
BIC: 0.007863
Training metrics:
R-squared: 0.992185
RMSE: 0.088400
MAE: 0.070176
Validation metrics:
R-squared: 0.992274
RMSE: 0.091000
MAE: 0.071396
Coefficients:
Intercept = -0.000001
b(1) = -0.066806
b(2) = -0.104624
b(3) = 0.946661
b(4) = -0.019752
b(5) = 0.041678
b(6) = -0.048295
b(7) = -0.009357
b(8) = -0.020131
b(9) = 0.029408
b(10) = 0.155854
VIF:
VIF(1) = 1.5706
VIF(2) = 2.2867
VIF(3) = 9.9995
VIF(4) = 2.1403
VIF(5) = 1.3111
VIF(6) = 1.0642
VIF(7) = 2.8821
VIF(8) = 8.3608
VIF(9) = 2.4643
VIF(10) = 2.7155この出力では以下の情報が提供されています:
- リッジパラメータ (h): 0.000009 - これは正則化の強さを示します。
- BIC (ベイズ情報量基準): 0.007863 - モデルの適合度と複雑さのバランスを評価します。
- 学習および検証データに対する性能指標 (R-squared, RMSE, MAE)
- モデル係数:
- Intercept (切片): -0.000001
- b(1) から b(10): 各特徴量に対応する係数。例えば、b(3) = 0.946661 は時間の周期性(cos)の係数で、最も大きな影響を持つことがわかります。
- VIF (分散拡大要因): 各特徴量の多重共線性を評価します。一般的に10未満が望ましいとされます。
係数とVIFの解釈
1時間後予測モデルの結果を例に取ると、以下のような解釈ができます:
- すべての特徴量のVIFが10未満であることから、深刻な多重共線性の問題はないと判断しました。
- 係数の絶対値が最も大きいのは b(3) = 0.946661 で、これは時間の周期性(cos)を表す特徴量です。この特徴量が最も予測に大きな影響を与えていることがわかります。
- 次に影響が大きいのは b(10) = 0.155854 で、過去12時間の温度の標準偏差を表しています。
- 切片(Intercept)がほぼ0であることから、特徴量の標準化が適切に行われたことが確認できます。
予測時間のモデル性能
各予測時間のモデル性能の一部抜粋は以下の通りです:
1時間後予測モデル:
- 訓練データ:R-squared = 0.992185, RMSE = 0.088400, MAE = 0.070176
- 検証データ:R-squared = 0.992274, RMSE = 0.091000, MAE = 0.071396
6時間後予測モデル:
- 訓練データ:R-squared = 0.993912, RMSE = 0.078009, MAE = 0.059300
- 検証データ:R-squared = 0.993913, RMSE = 0.080778, MAE = 0.061027
12時間後予測モデル:
- 訓練データ:R-squared = 0.965930, RMSE = 0.184543, MAE = 0.144814
- 検証データ:R-squared = 0.966563, RMSE = 0.189354, MAE = 0.146616
これらの結果から、モデルが短期予測(1-6時間後)で非常に高い精度を示し、長期予測(12時間後)でもかなり良好な性能を維持していることがわかります。また、訓練データと検証データでの性能が近いことから、モデルが過学習とはなっていないことも示唆されています。
予測誤差の解釈
例えば、6時間後予測モデルの検証データでのRMSE(0.080778)を実際の温度スケールに変換すると:
実際の温度スケールでのRMSE = 0.080778 * 8.243115956205 = 0.665893℃
つまり、6時間後の予測では平均して約0.67℃の誤差があることを意味します。
特徴量の重要度分析
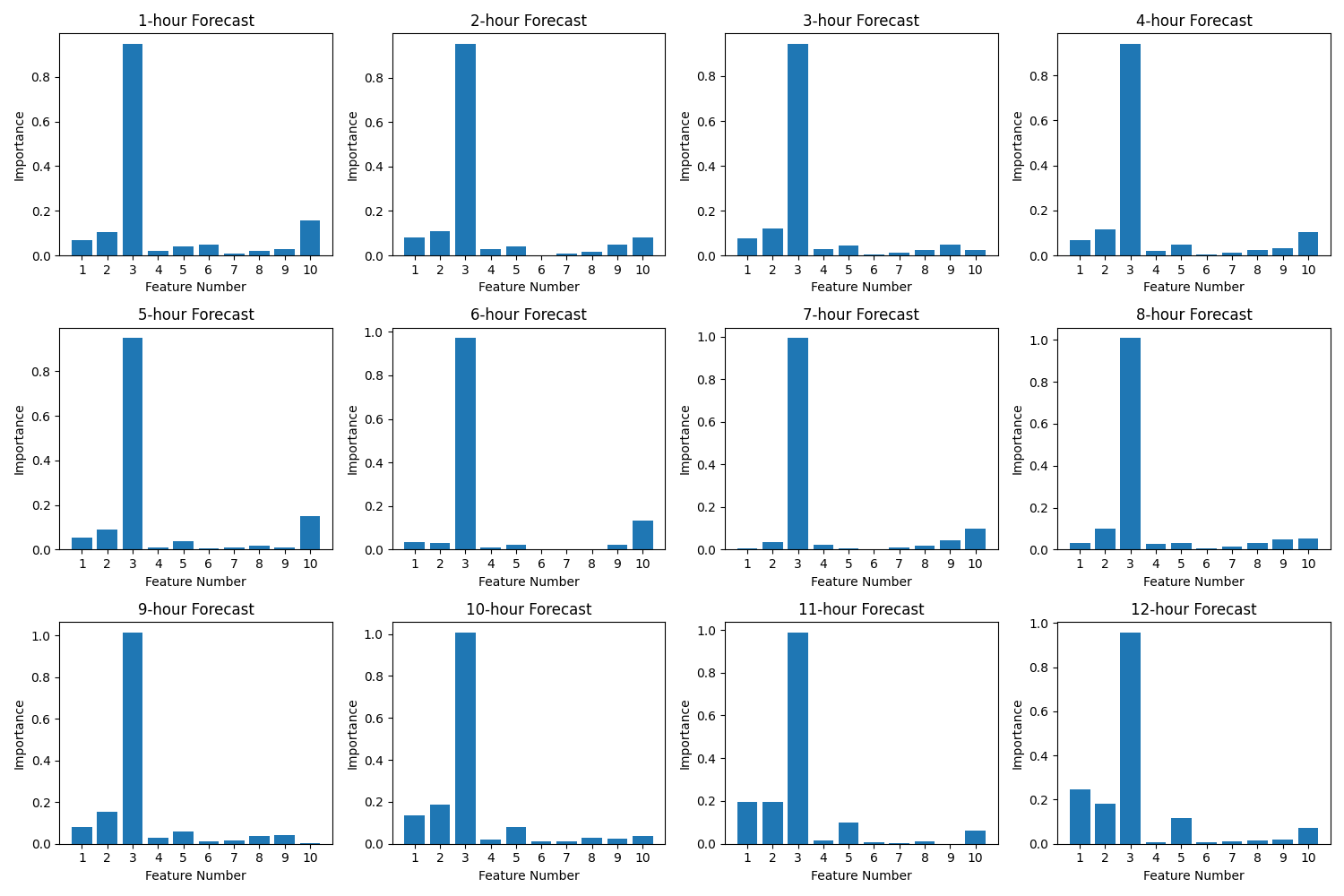
この図は、各予測時間(1時間後から12時間後まで)における特徴量の重要度を示しています。特徴量3(時間の周期性(cos))が全ての予測時間において最も重要であることが分かります。また、予測時間が長くなるにつれて、特徴量1(1時間前の気温)の重要度が低下し、特徴量10(過去12時間の温度の標準偏差)の重要度が上昇する傾向が見られます。
予測結果の可視化と分析
予測時間ごとの決定係数の推移
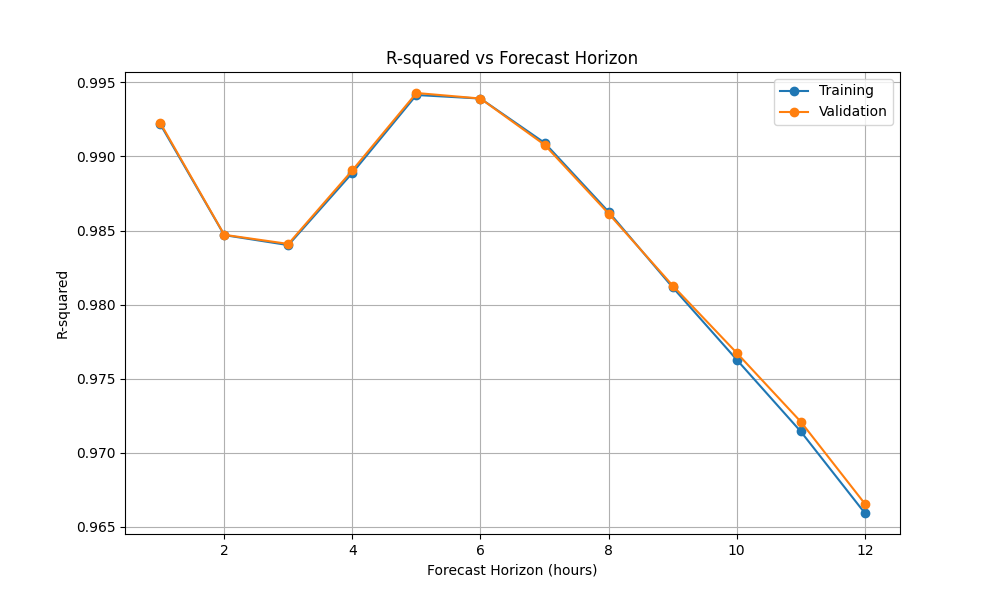
このグラフは、予測時間が長くなるにつれて決定係数がどのように変化するかを示しています。青線が学習データ、赤線が検証データの結果を表しています。
以下の点が注目されます:
短期予測の高精度:1時間後から6時間後までは両データセットで非常に高い精度(決定係数 > 0.99)を維持しています。
緩やかな低下:6時間以降、予測時間が長くなるにつれて決定係数は緩やかに低下していきますが、12時間後でも0.96以上の高い値を保っています。
学習と検証の一致:興味深いことに、検証データの決定係数が学習データとほぼ同等、あるいはわずかに上回っています。
モデルの汎化性能と適合性:検証データでの性能が学習データに近い事から、このモデルが高い汎化性能を持っていることが示唆されます。
このグラフは、開発したモデルが短期から中期(12時間)までの予測に対して高い精度を維持し、未見のデータに対しても安定した性能を発揮できることを示しています。
実測値と予測値の散布図
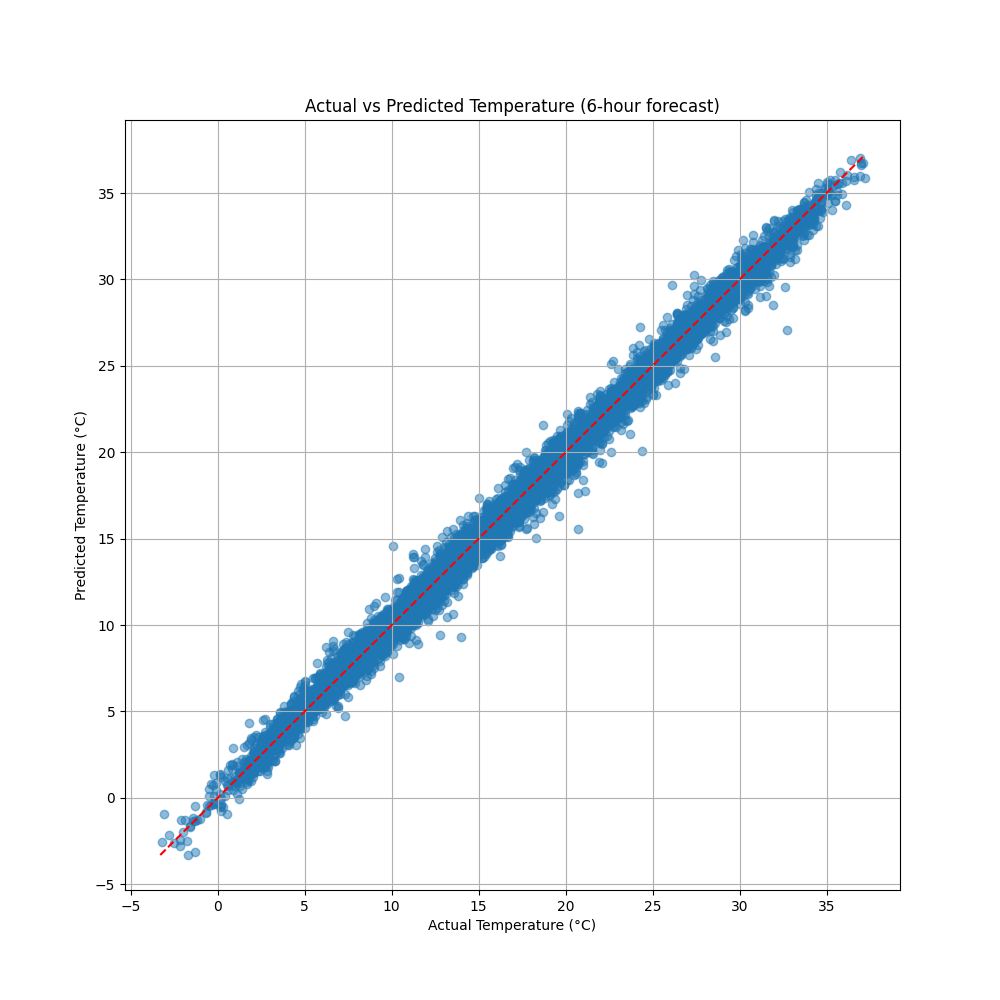
このグラフは、2023年の検証データにおける6時間後の予測値と実測値の関係を示しています。点が対角線上に集中していることから、予測値が実測値とよく一致していることがわかります。
時系列での実測値と予測値の比較

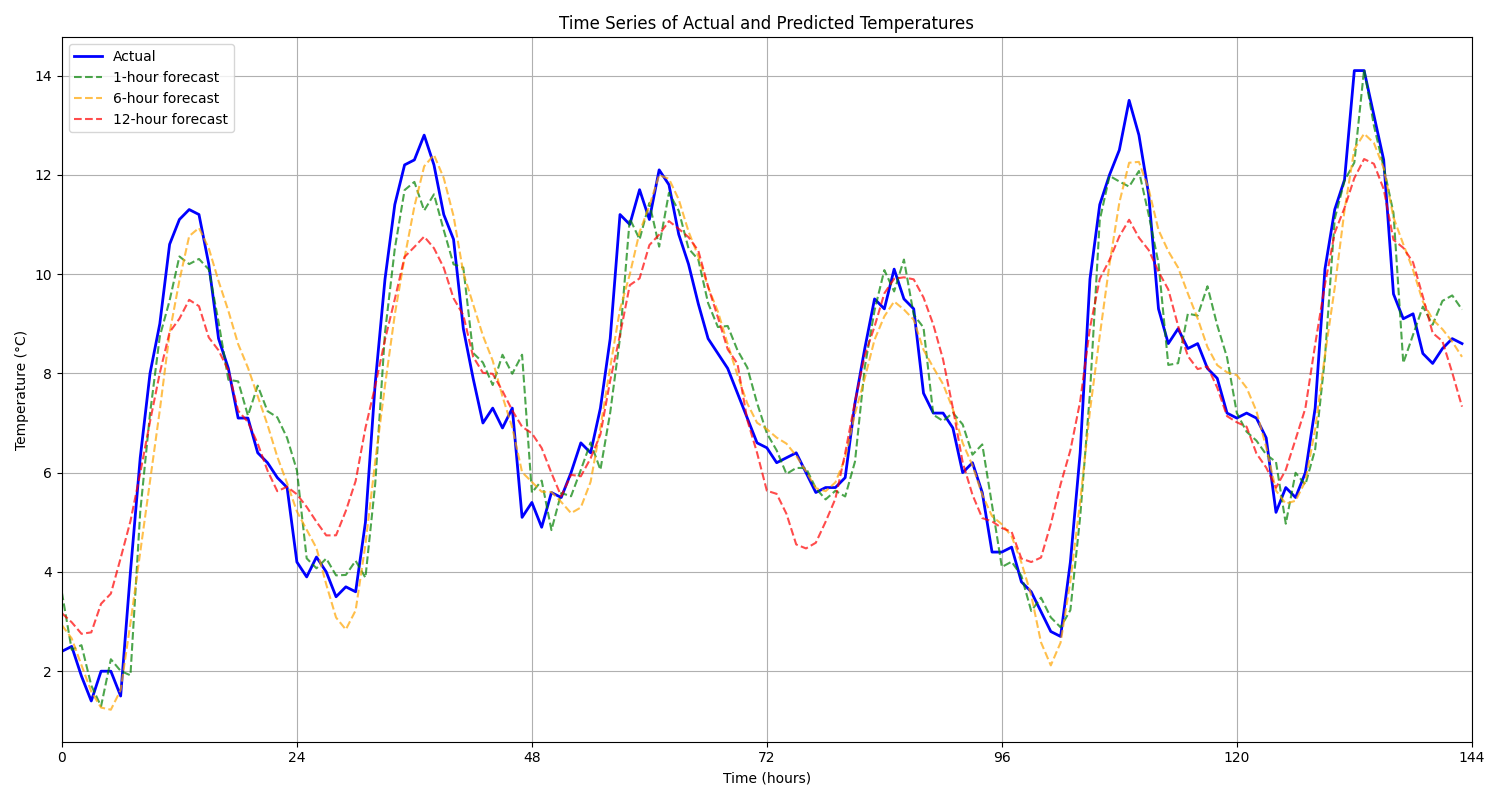
この図は、実際の気温と1時間後、6時間後、12時間後の予測値を時系列で比較しています。1時間後の予測は実測値にほぼ一致していますが、予測時間が長くなるにつれて誤差が大きくなる傾向が見られます。特に、急激な温度変化や極値の予測が難しくなっています。
このグラフを「予測誤差分布図」として追加し、以下のような説明を加えることをお勧めします:予測誤差の分布
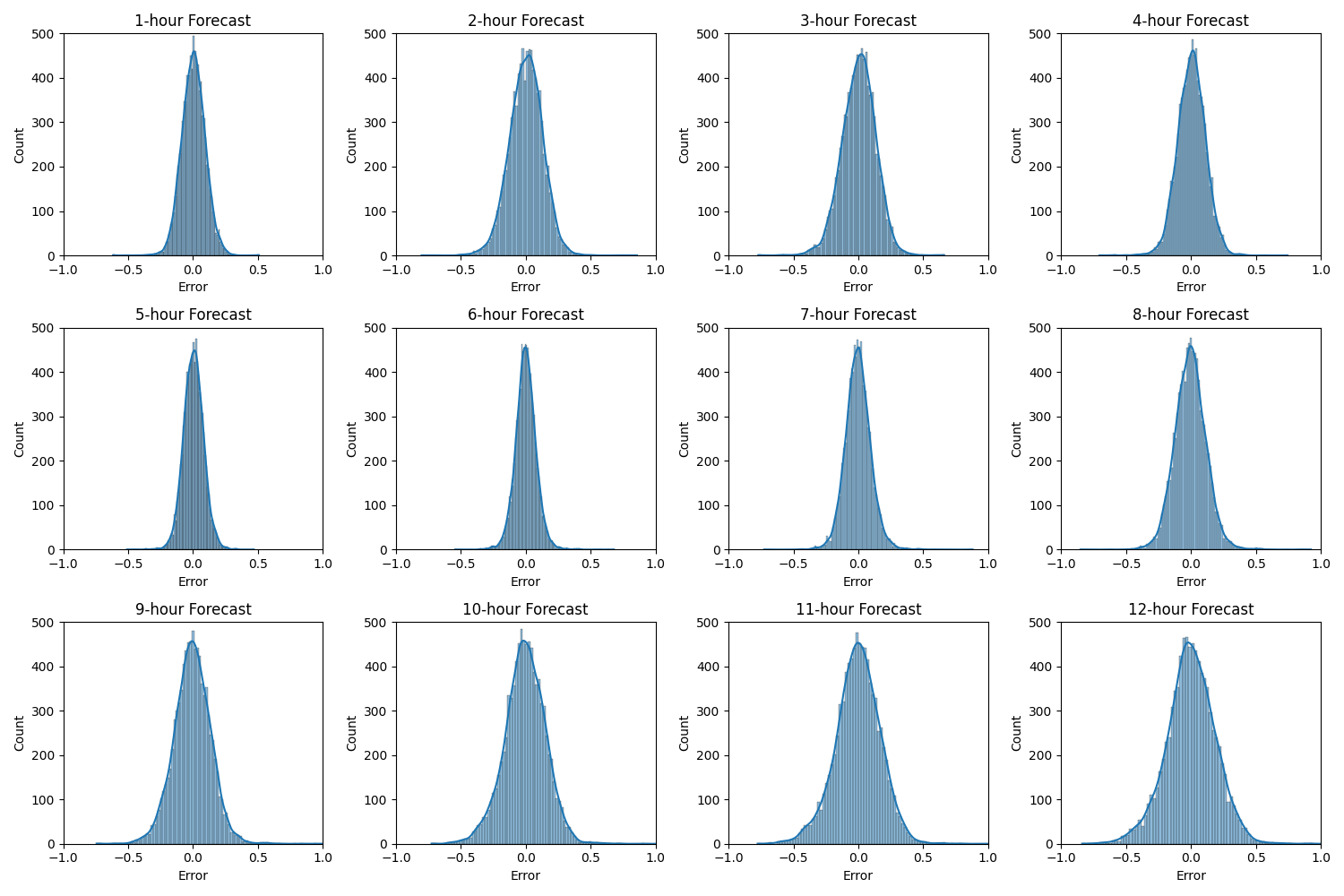
この図は、1時間後から12時間後までの各予測時間における誤差の分布を示しています。各グラフのx軸は予測誤差(実測値 - 予測値)を、y軸は頻度を表しています。
以下の特徴が観察できます:
対称性:全ての予測時間において、誤差分布がほぼ0を中心に対称的であることがわかります。これは、モデルが系統的な過大予測や過小予測を行っていないことを示唆しています。
誤差の増大:予測時間が長くなるにつれて、分布の幅が広がっています。これは、長期予測になるほど誤差が大きくなる傾向を示しています。
正規分布的形状:ほとんどの分布が正規分布に近い形状を示しています。これは、モデルの誤差が適切に振る舞っていることを示唆し、統計的な信頼性を支持しています。
外れ値の存在:特に長期予測(例:12時間後)では、分布の裾野が広がり、比較的大きな誤差も稀に発生していることがわかります。
この誤差分布の分析から、モデルが短期予測では非常に精度が高く、長期予測になるにつれて誤差が徐々に大きくなるものの、全体的に安定した予測を行っていることが確認できます。また、誤差の対称性は、モデルがバイアスなく予測を行っていることを示唆しています。
結論と今後の展望
本プロジェクトでは、Fortranとリッジ回帰を用いて、過去24時間の毎時データから最大12時間先までの気温を高精度で予測するモデルを構築しました。
特筆すべき成果:
- 短期予測(1-6時間後)で高い精度(決定係数 > 0.99)を達成
- 12時間後予測でも高い精度(決定係数 > 0.96)を維持
- 2023年の未知データでも同等の性能を示し、高い汎化性能を実証
- 6時間後予測で平均約0.67℃の誤差という実用的な精度を実現
今後の課題と展望:
- より長期の予測モデルの開発
- 他の気象要素(湿度、気圧、風速、風向、日照時間、など)の組み込みによるモデルの拡張
- 異なる地域や気候帯でのモデルの適用と比較
- 深層学習モデル(LSTM, Transformerなど)との性能比較
本プロジェクトを通じて、Fortranの高速な数値計算能力と機械学習的手法を組み合わせることで、高精度な気象予測が可能であることを示しました。 特に、本モデルの特徴である「過去24時間の連続したデータと日時情報のみを用いて1-12時間先までの予測が可能」という点は、限られたデータでの予測が必要な場面で利点となります。
