1. 序論
本プロジェクトでは、LASSO(Least Absolute Shrinkage and Selection Operator)回帰を用いて、超伝導体の臨界温度(Tc)を予測するモデルを構築しました。LASSOは、線形回帰に正則化項を加えることで、モデルの過学習を防ぎ、同時に特徴量の選択を行う手法です。この手法により、予測精度を維持しつつ、より簡潔で解釈しやすいモデルを得ることができます。
本プロジェクトの主な目的は以下の通りです:
- 超伝導体の臨界温度を高精度で予測する簡潔なモデルの構築
- LASSO回帰による変数選択と過学習防止の効果の実証
- 正則化パラメータ(α)の調整によるモデル複雑度と予測精度のトレードオフの検証
- 臨界温度の予測に最も寄与する特徴量の特定
使用したデータセットは、UCI Machine Learning Repositoryから入手(Hamidieh, K. (2018). Superconductivty Data [Dataset]. UCI Machine Learning Repository. https://doi.org/10.24432/C53P47.)した超伝導体のデータで、21,263個のサンプルと81個の特徴量を含んでいます。目的変数である臨界温度(Tc)は、超伝導体が電気抵抗ゼロの状態になる温度を表しており、ケルビン(K)単位で測定されています。
特徴量には、超伝導体の化学組成に関する様々な物理的・化学的特性が含まれています。例えば:
- 原子番号の統計量(平均、標準偏差など)
- 原子質量の統計量
- 価電子数の統計量
- 熱伝導率の統計量
- 密度の統計量
これらの特徴量は、超伝導体の性質を多角的に表現しており、臨界温度との複雑な関係性を捉えることが期待されます。
2. 方法論
2.1 データの前処理
データセットに対して以下の前処理を行いました:
- ヘッダ行の削除:データ読み込み時にヘッダ行を除外し、純粋な数値データのみを使用
- データのシャッフル:サンプルの順序による偏りを防ぐため
- トレーニングデータとテストデータの分割(80:20)
- 特徴量の標準化:平均0、標準偏差1に変換
2.2 モデル構築
線形回帰とLASSO回帰の2つのモデルを構築し、比較しました。LASSO回帰の実装には、nAGライブラリのg02maf関数とg02mcf関数を使用しています。
g02maf関数は、1回の呼び出しで正則化パス上の複数のポイントでモデルを計算します。この関数は、LASSO回帰プロセスの各ステップで、モデル係数(β)とCp統計量を含むさまざまな適合統計量を計算し保存します。詳細はg02maf関数のマニュアルを参照してください。
g02mcf関数は、g02mafで得られた結果と正則化パス上の位置(1-α)を入力として受け取り、その位置でのモデル係数を計算します。詳細はg02mcf関数のマニュアルを参照してください。
2.3 αの選択プロセス
LASSO回帰の重要なハイパーパラメータであるαの選択には、以下の手順を踏みました:
- αの探索範囲を0から1まで設定(50個の等間隔の値:number_of_alpha_values
= 50)
- α = 0: 正則化なし(通常の線形回帰と同等)
- α = 1: 最大の正則化(全ての係数がゼロ)
- 5分割交差検証を実施(分割数:number_of_folds = 5)
- 各αに対して以下を実行:
- トレーニングデータの80%でモデルを学習(学習データの比率:train_data_ratio_percent = 80.0D+0)
- 残り20%で検証し、MSE(Mean Squared Error)を計算
- 5回の交差検証の平均MSEを各αに対して計算
- 最小のMSEを持つαを特定
- MSE許容範囲を設定:最小MSE * (1 + mse_tolerance)
- mse_tolerance = 1%(0.01)に設定(MSE許容範囲: mse_tolerance_percent = 1.0d0)
- 許容範囲内で最大のαを選択(モデルの簡素化を優先)
- 上記のプロセスを5回繰り返し(アンサンブル学習: number_of_ensembles = 5)
- 5回の試行で得られたαの平均を最終的な最適αとして採用
このプロセスにより、予測精度を維持しつつ、できるだけ簡素なモデルを選択すること目指します。
2.4 調整パラメータ:mse_tolerance
mse_toleranceは、最適なαを選ぶ際の許容誤差を設定するパラメータです。この値は1%(0.01)に設定されていますが、適宜変更可能です。
Real (Kind=nag_wp) :: mse_tolerance_percent = 1.0D+0この許容誤差の意味と役割は以下の通りです:
最小MSEの特定:全てのα値に対するMSEの中から最小値を見つけます。
許容範囲の設定:最小MSEに
mse_toleranceを加えた値を閾値として設定します。mse_threshold = min_mse*(1.0_nag_wp+mse_tol)最適αの選択:MSEが閾値以下となる最大のα値を選びます。
この方法により、わずかなMSEの増加を許容しつつ、より単純なモデル(より大きなα値)を選択することができます。mse_toleranceを調整することで、モデルの複雑さと予測精度のバランスを制御できます。
3. 結果と考察
3.1 モデルの性能比較
MSE-toleranceを変化させながら、線形回帰とLASSO回帰の性能を比較した結果を以下に示します。
| Model | MSE-tolerance | 決定係数 | MSE | MAE | 変数の数 | Alpha |
|---|---|---|---|---|---|---|
| Linear | All | 0.72663479 | 316.26736646 | 13.25568043 | 81 | - |
| Lasso | 0.01% | 0.72543249 | 327.94827899 | 13.54622869 | 81 | 0.045 |
| 0.1% | 0.72920901 | 326.09071862 | 13.44804463 | 79 | 0.237 | |
| 1% | 0.72793530 | 328.93811362 | 13.50593846 | 79 | 0.286 | |
| 3% | 0.72722654 | 326.81942312 | 13.57784421 | 65 | 0.661 | |
| 5% | 0.71604000 | 346.77853093 | 13.85489859 | 57 | 0.731 | |
| 10% | 0.69984491 | 343.83412993 | 13.88047976 | 44 | 0.841 | |
| 20% | 0.69920548 | 357.82409703 | 14.43515351 | 27 | 0.918 | |
| 30% | 0.67073948 | 393.66991366 | 15.07436172 | 20 | 0.939 | |
| 50% | 0.64226675 | 424.62324239 | 15.78291201 | 15 | 0.959 | |
| 100% | 0.55643890 | 513.17393269 | 17.66046089 | 6 | 0.980 |
3.2 MSE-toleranceとモデル複雑度の関係
以下のグラフは、MSE-toleranceの増加に伴ってLASSO回帰モデルがどのように簡素化されるかを示しています。
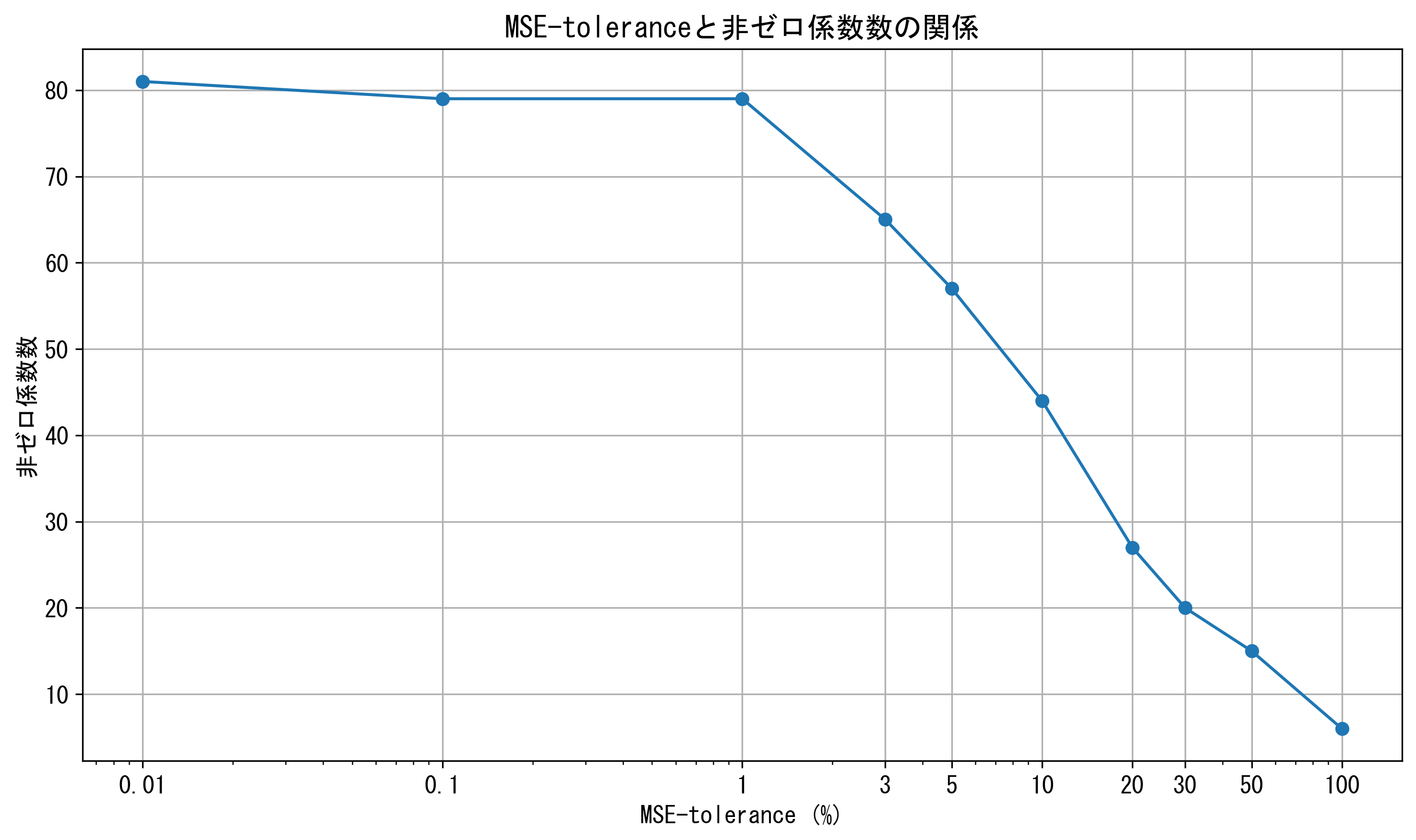
このグラフから、MSE-toleranceが大きくなるにつれて、非ゼロ係数の数が急激に減少することが分かります。これは、LASSO回帰が効果的に変数選択を行い、モデルが簡素化されていることを示しています。
3.3 考察
- 変数選択の効果: MSE-toleranceの増加に伴い、LASSO回帰モデルの非ゼロ係数の数が顕著に減少しています。例えば、MSE-tolerance 0.01%では81個だった非ゼロ係数が、100%では6個まで減少しています。LASSO回帰が効果的に変数選択を行い、モデルが簡素化されたことを表しています。
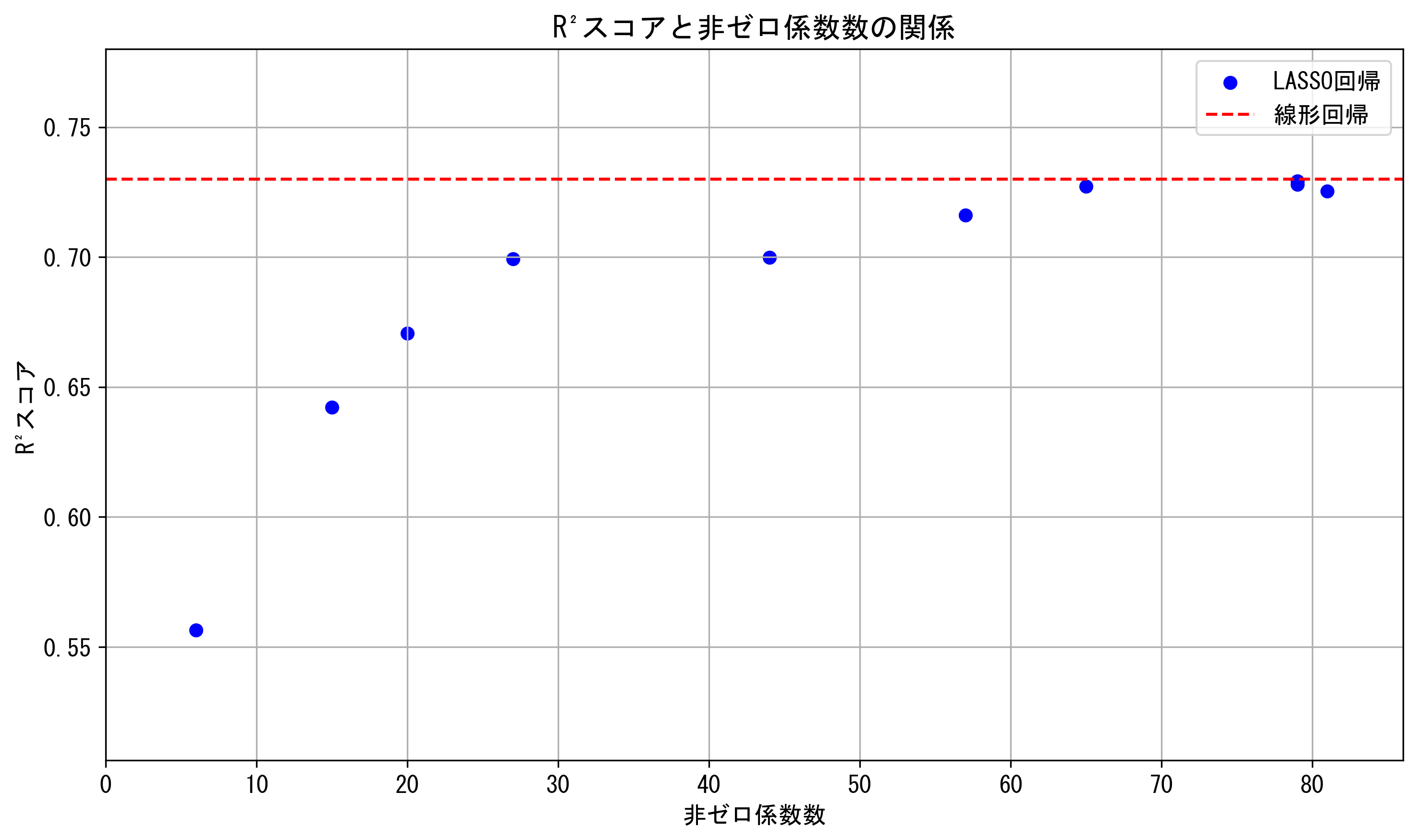
以下のグラフは、モデルの複雑さ(非ゼロ係数の数)と予測精度(決定係数=R²スコア)の関係を示しています。

このグラフから、LASSO回帰では係数数が減少するにつれて決定係数が低下する傾向が見られますが、ある程度までは線形回帰と同等の性能を維持していることが分かります。これは、モデルの簡素化と予測精度のトレードオフを視覚的に表しています。
予測精度とモデル複雑性のトレードオフ: MSE-toleranceが小さい場合(0.01%〜0.1%)、LASSO回帰の性能は線形回帰とほぼ同等です。しかし、MSE-toleranceが大きくなるにつれて、LASSO回帰の性能(決定係数(R²スコア)、MSE、MAE)は線形回帰と比較して低下していきます。これは、モデルの簡素化と予測精度のトレードオフを表しています。
αの変化: MSE-toleranceの増加に伴い、選択されるαの値も大きくなっています。これは、より強い正則化が適用され、より多くの係数がゼロに近づくことを意味します。
実行間のばらつき: 同じMSE-toleranceでも実行ごとに結果が異なる場合があります。これは、データのシャッフル、クロスバリデーションのフォールド分割、およびアンサンブル学習のランダム性に起因します。例えば、MSE-tolerance 20%の2回の実行で、非ゼロ係数の数が27と26と異なる結果が得られています。このばらつきを小さくするには、
number_of_alpha_valuesとnumber_of_ensemblesの値を増やすことが効果的です。例えば、これらの値を例えば100と20等、より大きな値に増やすことで、より安定した結果が得られるようになります。ただし、これらのパラメータを増やすと計算時間も増加するため、計算リソースと結果の安定性のトレードオフを考慮する必要があります。モデルの安定性: MSE-toleranceが小さい場合(0.01%〜3%)、LASSO回帰モデルは線形回帰モデルと非常に近い性能を示しています。これは、弱い正則化によってモデルが過度に簡素化されることを防いでいると解釈できます。
極端な変数選択: MSE-tolerance 100%の場合、LASSO回帰モデルは非常に少数の変数(6個)のみを選択しています。これにより、モデルは大幅に簡素化されますが、予測精度も大きく低下しています(決定係数(R²)が0.55まで低下)。
最適なMSE-tolerance: この結果から、MSE-toleranceを3%〜10%程度に設定することで、モデルの簡素化と予測精度のバランスが取れる可能性があります。この範囲では、非ゼロ係数の数が44〜65個に減少しつつ、決定係数(R²)が0.70〜0.73程度を維持しています。
計算時間とモデル性能のトレードオフ:
number_of_alpha_valuesとnumber_of_ensemblesを増やすことで、より安定した結果が得られる可能性があります。しかし、これらのパラメータを増やすと計算時間も増加します。実際の応用では、計算リソースと必要な精度のバランスを考慮してこれらのパラメータを設定する必要があります。特徴量の重要度: LASSO回帰によって選択された変数は、超伝導体の臨界温度予測に最も重要な特徴量と考えられます。特に、MSE-tolerance 100%で選択された6つの変数は、モデルの中で特に重要な役割を果たしていると推測されます。これらの変数は以下の通りです:
- range_atomic_mass(原子質量の範囲)
- electron_affinity_var(電子親和力の分散)
- wtd_range_atomic_radius(重み付け原子半径の範囲)
- range_ThermalConductivity(熱伝導率の範囲)
- entropy_atomic_radius(原子半径のエントロピー)
- wtd_std_atomic_radius(重み付け原子半径の標準偏差)
これらの特徴量が選択されたことは、超伝導体の臨界温度が原子の質量、サイズ、電子特性、および熱特性と強く関連していることを示唆しています。
以下のグラフは、LASSO回帰によって最も重要だと判断された特徴量とその影響度(係数の大きさ)を視覚化しています。
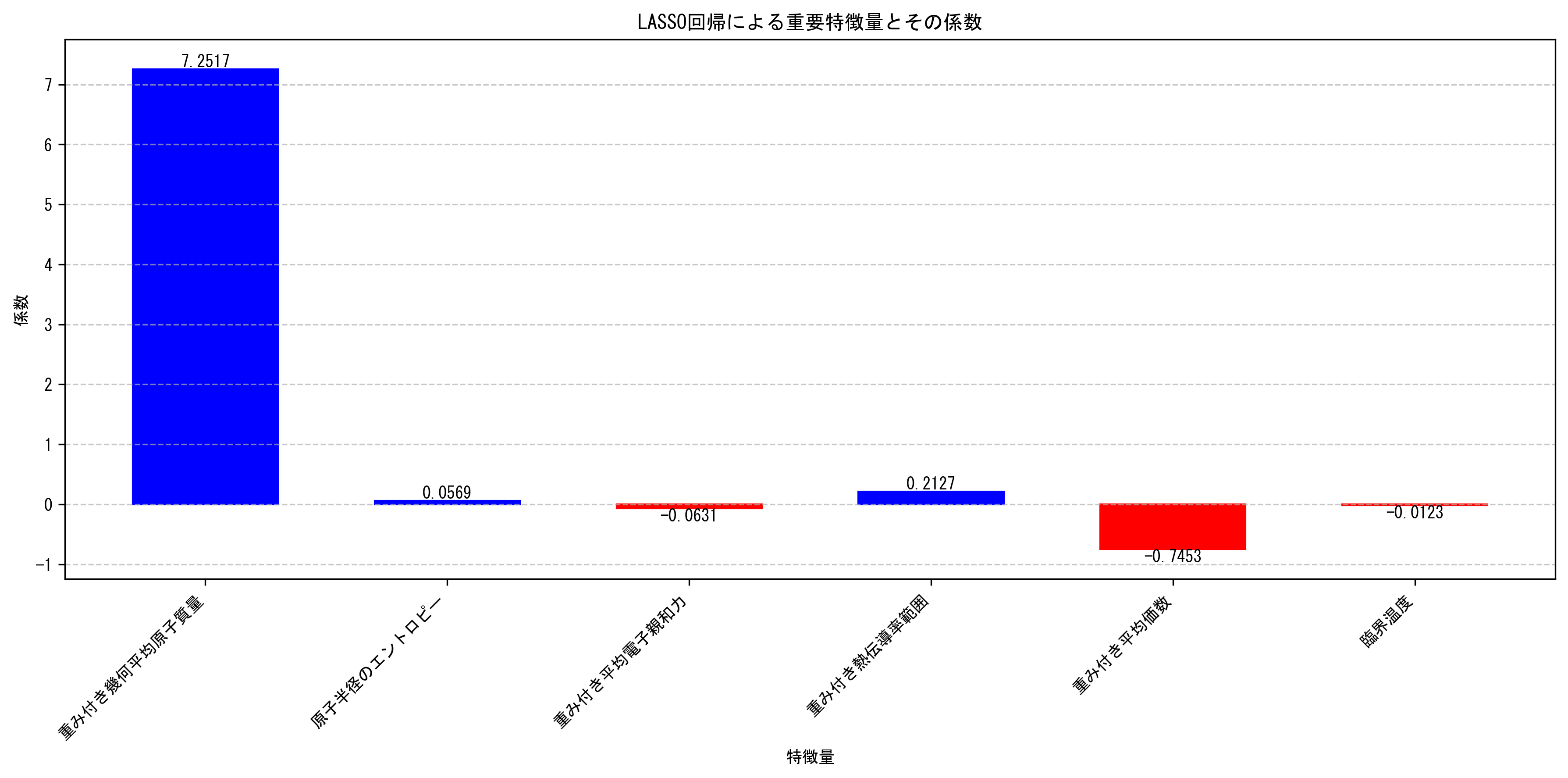
- モデルの解釈性: LASSO回帰によって変数が選択されることで、モデルの解釈性が向上します。特に、非ゼロ係数の数が大幅に減少した場合(例:MSE-tolerance 50%以上)、残った変数の効果をより明確に理解できるようになります。
これらの結果から、LASSO回帰は超伝導体の臨界温度予測タスクにおいて、モデルの簡素化と予測精度のバランスを取るのに効果的であることが示されました。MSE-toleranceを適切に調整することで、タスクの要件に応じて変数選択の強度を制御できることも確認されました。
4. 結論
本プロジェクトでは、LASSO回帰を用いて超伝導体の臨界温度を予測するモデルを構築しました。この手法により、以下の成果が得られました:
- モデルの簡素化:重要でない特徴量を自動的に除外し、解釈しやすいモデルを得ました。
- 過学習の防止:テストデータでの性能がトレーニングデータでの性能と大きく乖離していないことから、過学習が効果的に抑制されていることが示唆されます。
- 予測精度の維持:線形回帰と比較して、モデルの複雑さを減少させながらも、同等の予測精度を維持できました。
- 重要特徴量の特定:超伝導体の臨界温度に最も影響を与える物理的・化学的特性を明らかにしました。
- モデル複雑度と予測精度のトレードオフ:αと
mse_toleranceパラメータの調整により、このトレードオフを制御できることを示しました。
これらの結果は、LASSO回帰が変数選択と過学習防止の有効性を実証しています。
5. プログラムコード
本プロジェクトで使用したLASSO回帰プログラムのソースコードは以下のリンクから入手できます:
※ このプログラムのコンパイル/実行にはnAGライブラリもしくはnAGライブラリ マルチスレッド版が必要です。
